Foundations of Probability
- Setting the Stage: Sample Space, Events, and Probability
- Bayes’ Theorem: Updating Beliefs with Evidence
- Quantifying Outcomes: Random Variables
- Describing Distributions: Expectation, Variance, and Standard Deviation
- A Distribution-Agnostic Bound: Chebyshev’s Inequality
- The Wisdom of Crowds: The Law of Large Numbers (LLN)
- The Ubiquitous Bell Curve: The Central Limit Theorem (CLT)
- Bringing It Together: Applications in Machine Learning
- Wrapping Up
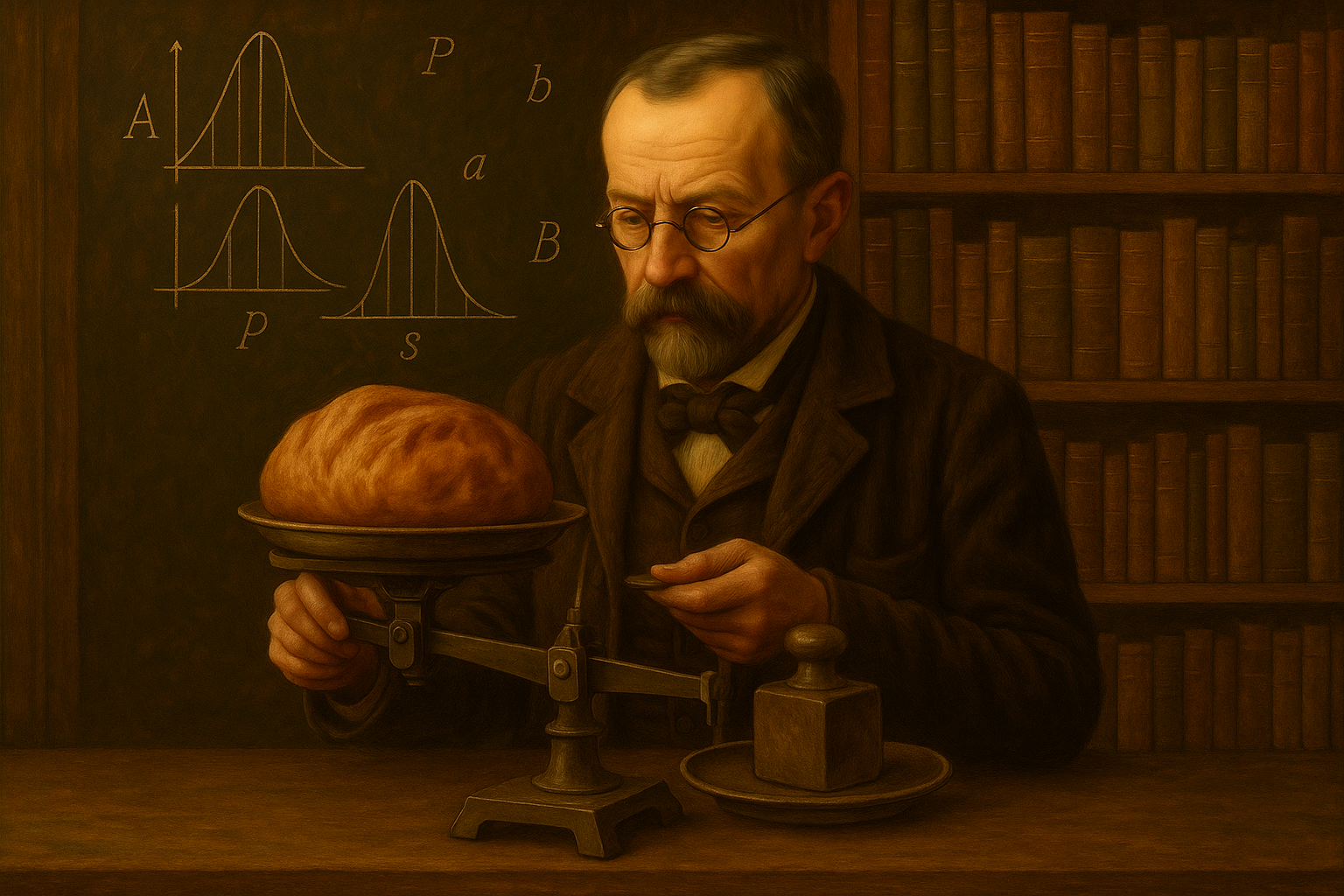
Consider a challenge faced by the renowned French mathematician Henri Poincaré. Poincaré would regularly purchase a loaf of bread from his local baker, expecting each loaf to weigh precisely 1 kilogram as advertised. However, being a keen observer, he began to suspect he was consistently receiving less than the promised amount. This wasn’t a one-time suspicion; it was a pattern he noticed over many purchases. To investigate, Poincaré meticulously weighed every single loaf he bought over the course of a year, essentially collecting a dataset of bread weights. When he eventually took the baker to court, his evidence was simple but powerful: the average weight of the loaves he had purchased was less than the stipulated 1 kg. Presented with this clear statistical summary, the court found in Poincaré’s favor and fined the baker.
Undeterred but seemingly having learned his lesson, the baker decided to be more careful. Over the following year, he ensured that the average weight of the loaves sold to Poincaré came out to exactly 1 kg. However, Poincaré continued his practice of weighing each loaf. Upon returning to court a year later, Poincaré revealed a deeper insight. While the average weight was now correct, the distribution of the weights was highly unnatural. Instead of the weights varying randomly around the 1 kg mark, as one would expect from typical baking variations (perhaps following a bell-shaped curve), Poincaré showed the distribution was skewed. Most loaves were significantly under 1 kg, but this was cleverly balanced by a few loaves that were substantially over 1 kg, specifically given to Poincaré to manipulate the average. Poincaré argued that this peculiar distribution proved the baker was still deliberately making underweight loaves but was occasionally compensating with heavier ones to falsify the average for his most attentive customer. The court, grasping this sophisticated statistical argument about the data’s variability and distribution rather than just its average, again ruled against the baker, recognizing his subtle deception.
This story, often recounted to highlight the power of quantitative observation, beautifully illustrates a crucial point: understanding data goes far beyond calculating simple summaries like the average. It requires examining the variability, the distribution, and using this probabilistic perspective to make informed judgments and predictions in the face of uncertainty. Just like Poincaré dealing with the baker’s inconsistent weights, when we build machine learning models, we’re not just dealing with data points — we’re dealing with the uncertainty inherent in that data and the processes that generated it. Whether we’re classifying emails, predicting stock prices, or detecting fraud, our models are built on probabilistic foundations that allow them to reason under uncertainty.
This post will delve into the core probability theory concepts that serve as the bedrock for machine learning, deep learning, and artificial intelligence. We will systematically explore foundational ideas like sample space, events, random variables, expectation, variance, and powerful theorems like the Law of Large Numbers and the Central Limit Theorem. Crucially, we will demonstrate how these theoretical constructs translate directly into practical applications within the realm of ML, empowering you to understand and leverage uncertainty in your models.
Setting the Stage: Sample Space, Events, and Probability
To build our understanding of how probability underpins machine learning, we must start with the absolute fundamental building blocks. Imagine any process where the outcome isn’t predetermined – flipping a coin, rolling a die, or a customer clicking on an ad. These are all examples of experiments in probability.
-
Sample Space ( \(\Omega\) ): This is the set of all possible, distinct outcomes of a random experiment. It’s the complete universe of results. For a coin flip, \(\Omega = \{\text{Heads, Tails}\}\). For rolling a standard six-sided die, \(\Omega = \{1, 2, 3, 4, 5, 6\}\).
-
Event: An event is any specific outcome or collection of outcomes from the sample space that we are interested in. Mathematically, an event is a subset of the sample space. For the die roll example, the event “rolling an even number” corresponds to the subset \(\{2, 4, 6\} \subseteq \Omega\). The event “rolling a 1” is the subset \(\{1\} \subseteq \Omega\).
-
Probability Function (P): This is a function that assigns a numerical value between 0 and 1 (inclusive) to each event. This value represents the likelihood of that event occurring. A probability of 0 means the event is impossible, while a probability of 1 means the event is certain. The function must satisfy certain rules (axioms of probability), such as the probability of the entire sample space being 1 (\(P(\Omega) = 1\)) and the probability of mutually exclusive events being additive.
Let’s consider a simple, yet relevant, machine learning example: training a binary classifier to detect whether an email is spam.
- The experiment is receiving an email and classifying it.
- The Sample Space is the set of possible classification outcomes: \(\Omega = \{\text{spam}, \text{not spam}\}\).
- We can define Events like “the email is spam” (the event \(\{\text{spam}\}\)) or “the email is not spam” (the event \(\{\text{not spam}\}\)).
- A Probability Function would assign probabilities to these events based on our training data. For instance, we might estimate:
- \(P(\text{email is spam}) = 0.4\) (meaning 40% of emails in our dataset are spam)
- \(P(\text{email is not spam}) = 0.6\) (meaning 60% are not spam) Notice that \(P(\text{spam}) + P(\text{not spam}) = 0.4 + 0.6 = 1\), as the probabilities of all possible outcomes must sum to 1.
Independence
Understanding the relationship between events is crucial. Two events \(A\) and \(B\) are considered independent if the occurrence of one event provides absolutely no information about the likelihood of the other event occurring. Mathematically, this is defined as:
\[P(A \cap B) = P(A) \cdot P(B)\]Here, \(A \cap B\) represents the event where both \(A\) and \(B\) occur. If knowing that event \(B\) happened doesn’t change the probability of event \(A\), then they are independent.
In probability theory, we often use the notation \(X \perp Y\) to compactly express that random variables X and Y are independent. This “⊥” symbol comes from geometry (where it means perpendicular), and in this context, it captures the idea that two variables move in unrelated directions—they have no shared information.
In machine learning, the concept of independence (or more commonly, conditional independence) is a simplifying assumption used in models like Naive Bayes classifiers. Naive Bayes assumes that the presence or absence of a particular feature (e.g., a specific word in an email) is independent of the presence or absence of other features, given the class label (spam or not spam).
While this assumption is often not strictly true in real-world data, it dramatically reduces complexity. And surprisingly, Naive Bayes still performs well in many high-dimensional classification problems—especially in text and NLP tasks—thanks to the robustness of probabilistic reasoning even under imperfect independence.
Conditional Probability
Often, the probability of an event does depend on whether another event has already occurred. This is where conditional probability comes in. It quantifies the probability of event \(A\) happening given that event \(B\) has already taken place. We denote this as \(P(A \mid B)\), read as “the probability of A given B”.
The formula for conditional probability is:
\[P(A \mid B) = \frac{P(A \cap B)}{P(B)}, \quad \text{provided } P(B) > 0\]This formula essentially restricts our focus to the cases where \(B\) occurred (the event space becomes \(B\)) and asks what proportion of those cases also included \(A\) (the intersection \(A \cap B\)).
This concept is profoundly important and is the direct foundation of Bayes’ Theorem. Bayes’ Theorem allows us to update our belief (the probability) about an event based on new evidence. For example, if our spam filter sees the word “Viagra” in an email, it updates its initial probability that the email is spam, given the new information (the presence of that specific word). This iterative updating of probabilities as new data arrives is a core mechanism in many learning algorithms.
Bayes’ Theorem: Updating Beliefs with Evidence
Building directly upon the concept of \(\text{conditional probability}\), Bayes’ Theorem provides a fundamental way to revise existing probabilities—our beliefs—in light of new evidence. It’s a cornerstone of statistical inference and is absolutely vital in many areas of machine learning, particularly in Bayesian modeling.
Recall the formula for conditional probability:
\[P(A \mid B) = \frac{P(A \cap B)}{P(B)}\]Similarly:
\[P(B \mid A) = \frac{P(B \cap A)}{P(A)}\]Since \(A \cap B = B \cap A\), we have:
\[P(A \cap B) = P(B \mid A) \cdot P(A)\]Substituting this into the expression for \(P(A \mid B)\) gives Bayes’ Theorem:
\[P(A \mid B) = \frac{P(B \mid A) \cdot P(A)}{P(B)}\]Let’s break this down in the context of updating beliefs:
- \(P(A \mid B)\): the posterior probability — our updated belief about \(A\) after observing \(B\).
- \(P(A)\): the prior probability — our belief about \(A\) before observing any evidence.
- \(P(B \mid A)\): the likelihood — the probability of seeing evidence \(B\) if \(A\) is true.
- \(P(B)\): the evidence or marginal likelihood — the overall chance of observing \(B\), summed over all possibilities.
(By the law of total probability:
\(P(B) = \sum_i P(B \mid A_i) \cdot P(A_i)\), where \(A_i\) are mutually exclusive and exhaustive.)
Using the Spam Example
Let’s revisit our spam classifier. Suppose we want to compute the probability that an email is spam given that it contains the word "discount".
Let:
- \[A = \text{Email is spam}\]
- \[B = \text{Email contains the word 'discount'}\]
Then Bayes’ Theorem gives us:
\[P(\text{Spam} \mid \text{'discount'}) = \frac{P(\text{'discount'} \mid \text{Spam}) \cdot P(\text{Spam})}{P(\text{'discount'})}\]Breaking it down:
- \(P(\text{Spam}) = 0.4\) (based on overall frequency)
- \(P(\text{'discount'} \mid \text{Spam})\): the probability that a spam email contains “discount”
- \(P(\text{'discount'})\): the probability any email (spam or not) contains “discount”
- \(P(\text{Spam} \mid \text{'discount'})\): the updated probability the email is spam, given it contains “discount”
This is exactly how simple spam filters operate: updating the likelihood that a message is spam based on observed features like specific words.
Importance in Machine Learning
Bayes’ Theorem is central to Bayesian statistics and probabilistic modeling in ML:
- Bayesian Inference: Helps us update our beliefs about parameters (like weights in regression) as we see more data. We start with a prior, multiply it by a likelihood, and normalize to get the posterior.
- Naive Bayes Classifiers: Use conditional independence and Bayes’ Theorem to classify data efficiently, especially in text classification.
- Bayesian Networks: Graphical models where nodes represent variables and edges capture dependencies; all inference is done via Bayes.
- Sequential Learning & Decision Making: In reinforcement learning, agents update their understanding of the environment using Bayes’ rule as new observations come in.
In essence, Bayes’ Theorem gives us a principled framework to incorporate new evidence and revise our understanding of the world—which is exactly what machine learning is about.
Quantifying Outcomes: Random Variables
While sample spaces and events are useful for defining possible outcomes, ML models typically operate on numerical data. A random variable serves as the crucial bridge, mapping each outcome in our sample space to a numerical value. This allows us to apply mathematical and statistical operations to the results of our random experiments.
Formally, a random variable \(X\) is a function \(X: \Omega \to \mathbb{R}\) that assigns a real number to every outcome \(\omega \in \Omega\).
Random variables can be categorized based on the types of values they can take:
Discrete Random Variables
These are random variables that can only take on a countable number of distinct values. These values are typically integers, representing counts or categories.
Examples in ML contexts:
- The number of times a user clicks on an advertisement in a session (0, 1, 2, …).
- The outcome of a binary classification (0 for one class, 1 for the other).
- The number of errors a model makes on a test set.
For a discrete random variable \(X\), we describe the probability distribution using a Probability Mass Function (PMF). The PMF, denoted \(p(x)\) or \(P(X=x)\), gives the probability that the random variable \(X\) takes on a specific value \(x\):
\(P(X = x) = p(x)\) The sum of probabilities for all possible values must equal 1: \(\sum_x p(x) = 1\).
Continuous Random Variables
These are random variables that can take on any value within a given range or interval on the real number line. They represent measurements that can be arbitrarily precise.
Examples in ML contexts:
- The exact temperature reading from a sensor.
- A customer’s total spending amount on a website.
- The weight of a parameter in a neural network model.
For a continuous random variable, the probability of taking on any single specific value is technically zero. Instead, we describe the probability distribution using a Probability Density Function (PDF), denoted \(f(x)\). The PDF itself doesn’t give a probability, but the area under the curve of the PDF over an interval gives the probability that the random variable falls within that interval:
\(P(a \leq X \leq b) = \int_a^b f(x) \, dx\) The total area under the PDF curve must equal 1: \(\int_{-\infty}^{\infty} f(x) \, dx = 1\).
In machine learning, we frequently use random variables to model not just the data itself (e.g., assuming input features follow a certain distribution) but also the parameters of our models. For example, in Bayesian linear regression, we might assume the model’s weights are drawn from a Gaussian (Normal) distribution, which is a continuous probability distribution for a continuous random variable.
Describing Distributions: Expectation, Variance, and Standard Deviation
Once we have characterized the possible numerical outcomes using random variables, we need ways to summarize their distributions. Expectation, variance, and standard deviation are fundamental descriptive statistics that provide crucial insights into the central tendency and spread of a random variable’s values. They are building blocks for understanding model behavior and evaluating performance.
Expectation (\(\mathbb{E}[X]\))
The expectation (also known as the mean or expected value) of a random variable is essentially the weighted average of all possible values the variable can take, where the weights are the probabilities of those values occurring. It represents the center of mass or the average outcome if we were to repeat the experiment many, many times.
- For a discrete random variable \(X\) with PMF \(p(x)\): \( \mathbb{E}[X] = \sum_x x \cdot P(X = x) = \sum_x x \cdot p(x) \)
- For a continuous random variable \(X\) with PDF \(f(x)\): \( \mathbb{E}[X] = \int_{-\infty}^{\infty} x \cdot f(x) \, dx \)
In ML, the expected value is used in many contexts, such as calculating the expected loss of a model, or representing the average prediction value.
Variance (\(\text{Var}(X)\))
While the expectation tells us the center, the variance tells us about the spread or dispersion of the random variable’s values around its mean. A high variance indicates that the values are widely scattered, while a low variance suggests the values are clustered closely around the mean.
Mathematically, variance is the expected value of the squared difference between the random variable and its mean:
\(\text{Var}(X) = \mathbb{E}[(X - \mathbb{E}[X])^2]\) An alternative, often computationally easier, formula is: \(\text{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2\)
Understanding the variance of a model’s predictions or errors gives us critical insight into its uncertainty and consistency. A model with low prediction variance tends to make more consistent predictions for similar inputs, which is often desirable. High variance can indicate that the model is overly sensitive to noise in the training data (overfitting).
Standard Deviation (\(\sigma\))
The standard deviation is simply the square root of the variance:
\[\sigma = \sqrt{\text{Var}(X)}\]It’s often preferred over variance because it is expressed in the same units as the random variable itself and the mean, making it more intuitively interpretable as a measure of spread.
Standard deviation is commonly used in ML for:
- Feature scaling (Normalization): Scaling features to have zero mean and unit variance (standard deviation of 1) is a standard preprocessing step for many algorithms.
- Analyzing error distributions: Understanding the standard deviation of model errors helps in setting confidence intervals around predictions.
- Regularization: Techniques like L2 regularization are related to minimizing the squared magnitude of weights, which is connected to variance concepts.
A Distribution-Agnostic Bound: Chebyshev’s Inequality
We often encounter the Normal (Gaussian) distribution in statistics and machine learning, and it’s convenient because it comes with well-known rules of thumb regarding how much data falls within certain standard deviations from the mean (e.g., 68% within 1 std dev, 95% within 2 std devs). However, real-world data and model outputs don’t always follow a perfect normal distribution. What if the distribution is skewed, multimodal, or has heavy tails?
This is where Chebyshev’s Inequality provides a powerful guarantee. It’s remarkable because it requires very little information about the distribution – only its mean and finite variance – and still provides a lower bound on the probability that a random variable falls within a certain distance from its mean.
The Statement
For any random variable \(X\) (discrete or continuous) with a finite mean \(\mu = \mathbb{E}[X]\) and a finite variance \(\sigma^2 = \text{Var}(X)\), and for any positive constant \(k > 0\), the following inequality holds:
\[P(|X - \mu| \geq k\sigma) \leq \frac{1}{k^2}\]This inequality gives an upper bound on the probability that a value of \(X\) is more than \(k\) standard deviations away from the mean.
An equivalent and often more intuitive way to state it is:
\[P(|X - \mu| < k\sigma) \geq 1 - \frac{1}{k^2}\]This second form provides a lower bound on the probability that a value of \(X\) falls within \(k\) standard deviations of the mean.
Putting Numbers to It
Let’s plug in a few values for \(k\) to see the minimum proportion of data guaranteed to be within a certain range:
- For \(k = 2\): The probability that \(X\) is within 2 standard deviations of the mean is at least \(1 - \frac{1}{2^2} = 1 - \frac{1}{4} = 0.75\). This means at least 75% of the probability mass lies within the interval \([\mu - 2\sigma, \mu + 2\sigma]\).
- For \(k = 3\): The probability that \(X\) is within 3 standard deviations of the mean is at least \(1 - \frac{1}{3^2} = 1 - \frac{1}{9} \approx 0.889\). So, at least 88.9% of the probability mass lies within \([\mu - 3\sigma, \mu + 3\sigma]\).
Compare these minimum guarantees to the values for a Normal distribution:
- For a Normal distribution, approximately 95% of values are within 2 standard deviations.
- For a Normal distribution, approximately 99.7% of values are within 3 standard deviations.
As you can see, Chebyshev’s bound is more conservative than the bounds provided by the Normal distribution. This is because it applies universally to any distribution with finite mean and variance. It might “undershoot” for symmetric, unimodal distributions like the Gaussian, but the key and powerful point is that it always holds true, regardless of whether the distribution is skewed, lumpy, or heavy-tailed.
Why It Matters in Machine Learning
Chebyshev’s inequality, despite its simplicity, offers valuable robustness in ML contexts:
- Model Diagnostics and Error Bounds: Suppose you are analyzing the errors (residuals) of a regression model. If you don’t know the specific distribution of these errors (which is often the case), you can still use Chebyshev’s inequality with the calculated mean and variance of the residuals to get a guaranteed upper bound on the probability of seeing an error of a certain magnitude. This provides a safety net without making strong distributional assumptions.
- Outlier Detection: Chebyshev’s bound can help define what constitutes an “unusual” or potentially “outlying” value in a dataset or a model’s output in a way that doesn’t depend on assuming normality. If a data point is more than \(k\) standard deviations away from the mean, you can use the inequality to bound how rare such an observation is expected to be for any distribution.
- Robustness Checks: In applications where making specific distributional assumptions is risky (like fraud detection, cybersecurity, or safety-critical systems), Chebyshev’s inequality provides a mathematically solid, worst-case guarantee about the spread of your data or model predictions. You can make statements about probability bounds that are reliable even if the underlying process behaves unexpectedly, as long as its mean and variance are finite.
Think of Chebyshev as the ultimate pragmatist: it doesn’t need to know the fancy shape of the probability curve. It just needs the average and the spread, and it can still tell you something reliably true about how often values are far from the average. This is incredibly useful when the data refuses to conform to standard distributions.
The Wisdom of Crowds: The Law of Large Numbers (LLN)
The Law of Large Numbers is a fundamental theorem that connects theoretical probability to actual observed results. It explains why frequencies in real-world experiments tend to settle down to the theoretical probabilities over many trials.
The Law of Large Numbers states that as the number of independent and identically distributed (i.i.d.) random variables increases, their sample mean (the average of the observed values) converges towards the true expected value (the theoretical mean) of the underlying distribution.
Formally, for a sequence of i.i.d. random variables \(X_1, X_2, \dots, X_n\) with expected value \(\mathbb{E}[X] = \mu\), the sample mean \(\bar{X}_n = \frac{1}{n} \sum_{i=1}^n X_i\) converges to \(\mu\) as \(n \to \infty\).
\[\lim_{n \to \infty} \bar{X}_n = \mathbb{E}[X] = \mu\]There are different versions of the LLN (weak and strong convergence), but the core message is the same: averaging many random outcomes cancels out the randomness and reveals the underlying expected value.
Let’s visualize this powerful idea by simulating drawing samples from a simple distribution, like a uniform distribution between 0 and 1 (\(\mathcal{U}(0, 1)\)). The true mean (expected value) of this distribution is 0.5. We’ll compute the sample mean as we draw more and more samples and observe how it behaves.
import numpy as np
import matplotlib.pyplot as plt
# Reproducibility
np.random.seed(42)
# Generate 10,000 samples from a Uniform[0,1] distribution
samples = np.random.uniform(0, 1, 10000)
# Compute sample means as we increase sample size
# sample_means[i] is the mean of the first (i+1) samples
sample_means = [np.mean(samples[:i]) for i in range(1, len(samples) + 1)]
# Plotting
plt.figure(figsize=(10, 5))
plt.plot(sample_means, label='Sample Mean')
plt.axhline(y=0.5, color='red', linestyle='--', label='True Mean = 0.5')
plt.xlabel("Number of Samples")
plt.ylabel("Sample Mean")
plt.title("Illustration of the Law of Large Numbers")
plt.legend()
plt.grid(True, linestyle='--', alpha=0.6)
plt.show()
As clearly illustrated by the plot, the sample mean starts quite noisy and fluctuates significantly when the number of samples is small. However, as we increase the number of samples, the sample mean curve gradually settles down and converges closer and closer to the true mean of 0.5. This stabilization demonstrates the LLN in action – the random fluctuations average out over the long run.
ML Insight
The Law of Large Numbers provides the theoretical justification for why averaging the results of multiple models or multiple data points often leads to improved performance and stability in machine learning. In ensemble methods like Bagging (e.g., Random Forests), we train numerous models (decision trees) on different bootstrapped samples of the training data and average their predictions (or take a majority vote). Each individual tree might be noisy or have high variance, but the LLN guarantees that by averaging the predictions of a large number of these trees, the noise tends to cancel out, and the ensemble’s prediction converges towards the true underlying relationship, resulting in lower variance and better generalization on unseen data.
The Ubiquitous Bell Curve: The Central Limit Theorem (CLT)
If the Law of Large Numbers tells us that the sample mean converges to the true mean, the Central Limit Theorem (CLT) tells us what the distribution of the sample mean looks like when the sample size is large. It’s arguably one of the most powerful and surprising results in statistics, explaining why the Normal distribution appears so frequently in nature and data analysis.
Central Limit Theorem Statement: Given a set of independent, identically distributed (i.i.d.) random variables \(X_1, X_2, \dots, X_n\) with a finite mean \(\mu\) and finite variance \(\sigma^2\), as the sample size \(n\) becomes large, the distribution of the sample mean \(\bar{X}_n = \frac{1}{n} \sum_{i=1}^n X_i\) approaches a Normal (Gaussian) distribution, regardless of the original distribution of the individual variables \(X_i\).
More formally, the standardized sample mean approaches the standard normal distribution:
\(Z_n = \frac{\bar{X}_n - \mu}{\sigma / \sqrt{n}} \xrightarrow{d} \mathcal{N}(0,1) \quad \text{as } n \to \infty\)Here, \(\xrightarrow{d}\) means “converges in distribution”. The term \(\sigma / \sqrt{n}\) is the standard deviation of the sample mean, also known as the standard error.
This theorem is profound because it says that if you take the average of many random things, that average will tend to follow a normal distribution, even if the individual things you are averaging do not.
Let’s visualize the CLT. We will sample from a non-Gaussian distribution – the exponential distribution, which is highly skewed. We will then calculate the means of many independent samples (each of a fixed size, say 50) drawn from this exponential distribution and plot the distribution of these calculated means.
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Parameters for the exponential distribution (mean = scale)
scale_param = 1.0
true_mean_exp = scale_param
# Number of times to draw a sample of means
num_sample_means = 1000
# Size of each sample (must be large enough for CLT to start showing)
sample_size_per_mean = 50
# Draw multiple samples and calculate their means
means = []
for _ in range(num_sample_means):
# Draw a sample of size 'sample_size_per_mean' from Exponential distribution
sample = np.random.exponential(scale=scale_param, size=sample_size_per_mean)
# Calculate the mean of this sample
means.append(np.mean(sample))
# Plotting the histogram of the sample means
plt.figure(figsize=(10, 6))
sns.histplot(means, bins=30, kde=True, color='skyblue', edgecolor='black')
plt.title(f"Central Limit Theorem (CLT): Distribution of {num_sample_means} Sample Means (size={sample_size_per_mean}) from Exponential Distribution")
plt.xlabel("Sample Mean")
plt.ylabel("Frequency")
plt.axvline(x=true_mean_exp, color='red', linestyle='--', label=f'True Mean ({true_mean_exp:.1f})')
plt.legend()
plt.grid(True, linestyle='--', alpha=0.6)
plt.show()
The histogram clearly shows that even though the original exponential distribution was heavily skewed, the distribution of the sample means is remarkably bell-shaped, closely approximating a Normal distribution. This visual confirmation underscores the power of the CLT. The peak of the distribution of sample means is also centered around 1.0, the true mean of the Exponential(scale=1.0) distribution, consistent with the LLN.
ML Insight
The Central Limit Theorem explains why the Normal distribution is so fundamental and appears everywhere in machine learning and statistics.
- Parameter Estimates: Many parameters we estimate in ML models (like the weights in linear regression) are effectively averages or sums of influences from the training data. The CLT suggests that these estimates will often be approximately normally distributed, which allows us to construct confidence intervals and perform hypothesis tests on them.
- Model Errors: If the total error of a model is the sum of many small, independent error sources, the CLT predicts that the overall error distribution will tend towards a Normal distribution. This is why we often assume Gaussian noise in regression models.
- Statistical Inference: The CLT is the backbone of many statistical tests and confidence interval calculations used to evaluate model performance and compare different models. It allows us to make inferences about population parameters based on sample statistics, even if we don’t know the population distribution.
Bringing It Together: Applications in Machine Learning
Now that we’ve covered these fundamental probabilistic concepts, let’s explicitly connect them to how they are applied and why they are essential in practical machine learning workflows. These ideas aren’t just theoretical curiosities; they are the tools we use to build, understand, and trust our models.
Probabilistic Modeling
Many powerful ML models are inherently probabilistic, meaning they explicitly model the probability distributions of the data or the relationships between variables.
- Naive Bayes Classifiers: As discussed, they make strong (naive) conditional independence assumptions but are built directly on Bayes’ Theorem and conditional probabilities.
- Gaussian Mixture Models (GMMs): These models assume the data is generated from a mixture of several Gaussian distributions, using probability density functions to model clusters.
- Bayesian Linear Regression: Unlike standard linear regression which finds point estimates for parameters, Bayesian regression models the parameters themselves as random variables with probability distributions (priors and posteriors), using concepts of expectation, variance, and conditional probability (via Bayes’ rule).
Even complex modern models like Variational Autoencoders (VAEs) are deeply rooted in these basics, utilizing concepts like expectations, probability distributions (often assuming Gaussian latent spaces), and metrics like KL divergence which compare probability distributions.
Uncertainty Quantification
In many critical applications, a model’s prediction isn’t enough; we need to know how confident the model is in that prediction. Probability provides the language for this uncertainty quantification.
- Models that output probabilities (like the softmax layer in a neural network for classification, or probabilistic regression models) provide a complete distribution over possible outputs, not just a single point estimate.
- Knowing the variance of a model’s prediction distribution directly quantifies its spread and thus its uncertainty. A prediction with high variance is less certain than one with low variance.
- Using the principles from the CLT, we can often construct confidence intervals around predictions, giving a range within which the true value is likely to fall with a specified level of confidence.
This ability to quantify uncertainty is paramount in fields like medical diagnosis, financial forecasting, and autonomous systems, where the cost of an incorrect or overconfident prediction can be very high.
Why Empirical Means Work (Ensemble Models)
As highlighted when discussing the LLN, the success of many ensemble learning techniques is a direct consequence of probability theory.
- Bagging (e.g., Random Forests): By training multiple models on bootstrapped samples and averaging (regression) or voting (classification) their outputs, bagging reduces the variance of the final prediction. The Law of Large Numbers explains why this averaging process leads to a more stable and reliable estimate that converges towards the true underlying value.
- Boosting (e.g., XGBoost, LightGBM): While different from bagging, boosting also combines multiple weak learners. The final prediction is a weighted sum, and the properties of summing random variables (as suggested by the Central Limit Theorem) play a role in the distribution of the ensemble’s output and its error characteristics.
By aggregating the predictions of multiple diverse models, ensemble methods leverage the power of averaging noisy signals, leading to improved robustness, reduced overfitting, and better overall generalization performance.
Wrapping Up
Probability theory is far from being a dry, abstract mathematical subject when viewed through the lens of data science and machine learning. It is the essential language for understanding and working with uncertainty, which is inherent in real-world data and complex systems.
From the fundamental definitions of sample spaces and events, through the characterization of data using random variables, expectation, and variance, to the powerful guarantees provided by Chebyshev’s inequality, the convergence properties described by the Law of Large Numbers, and the widespread emergence of the Normal distribution explained by the Central Limit Theorem – these concepts are not just theoretical curiosities. They are the foundational pillars upon which countless machine learning algorithms and techniques are built. A solid understanding of these probabilistic foundations empowers you to not just use ML models, but to understand how they work, interpret their outputs (including their uncertainty), and design more effective solutions to challenging problems.
Next Up: Building upon these foundations, the next post in this series will take a deeper dive into Probability Distributions themselves. We will explore key distributions like the Bernoulli, Binomial, Poisson, and Gaussian in more detail, understanding their properties and how they are used to model different types of data and phenomena encountered in machine learning.