Probability Distributions
- Discrete Distributions
- Continuous Distributions
- Multivariate Distributions
- 0 Why We’re Leaving the Comfort of One Dimension
- 1 Joint Probability Distributions
- 2 Marginal Distributions – Solo Performances
- 3 Conditional Distributions – Slicing the Joint
- 4 Independence—When Roommates Ignore Each Other
- 5 Expectation Laws—Our Statistical Swiss Army Knife
- 6 Covariance & Correlation — Feeling the Sway in the Data
- 7 Beyond 2D: Vectors, Matrices, and Tensors
- Summary Table: Choosing the Right Distribution — Quick Cheat‑Sheet
Probability distributions shape how we simulate data, quantify uncertainty, and reason about model behavior. Whether you are generating synthetic samples, fitting probabilistic models, or understanding errors, distributions provide the structure for everything that follows.
In this post, we will explore:
- Important discrete and continuous distributions
- Concepts around multivariate distributions
- Key applications in machine learning and data science
Discrete Distributions
Discrete probability distributions represent outcomes that are countable — such as binary labels, event counts, or integer results of repeated trials. These are particularly relevant in classification tasks, anomaly detection, and simulations of real-world processes.
1. Bernoulli Distribution
The Bernoulli distribution is used to model a single trial with two possible outcomes: success (1) or failure (0). It is the building block of binary classification problems.
Probability Mass Function (PMF): \(P(X = x) = p^x (1 - p)^{1 - x}, \quad x \in \{0,1\}\)
Let \(X \sim \text{Bernoulli}(p)\)
This means:
- \[P(X = 1) = p\]
- \[P(X = 0) = 1 - p\]
- So, \(X \in \{0, 1\}\)
- Mean
We calculate: \(\mathbb{E}[X] = \sum_x x \cdot P(X = x)\)
Only two values of \(X\) matter: \(\mathbb{E}[X] = 0 \cdot (1 - p) + 1 \cdot p = p\)
- Variance
Definition: \(\text{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2\)
Since \(X \in \{0, 1\}\) and \(1^2 = 1, 0^2 = 0\):
\[\mathbb{E}[X^2] = 0^2 \cdot (1 - p) + 1^2 \cdot p = p\]So:
\[\text{Var}(X) = p - p^2 = p(1 - p)\]Applications:
- Binary classification (e.g., logistic regression target)
- Simulating binary labels for synthetic datasets
The plot below illustrates a Bernoulli distribution where the probability of success (1) is 0.7 and failure (0) is 0.3. This type of distribution is ideal for binary classification tasks where outcomes are either “yes” or “no”, such as predicting if a customer will churn. The interactive bar chart helps visualize how the probability is distributed between the two outcomes.
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
p = 0.7
samples = np.random.binomial(n=1, p=p, size=1000)
sns.countplot(x=samples)
plt.title(f"Bernoulli Samples (p = {p})")
plt.xlabel("Outcome")
plt.ylabel("Frequency")
plt.show()
Let’s say we’re modeling whether a customer clicks on an ad.
Success (click) = 1, Failure (no click) = 0
Suppose the click-through probability \(p = 0.3\).
Let’s compute the probabilities:
\[P(X = 1) = 0.3 \\ P(X = 0) = 1 - 0.3 = 0.7\]That’s it—just two outcomes.
Now compute:
- Mean: \(\mathbb{E}[X] = p = 0.3\)
- Variance: \(\text{Var}(X) = p(1 - p) = 0.3 \cdot 0.7 = 0.21\)
The Bernoulli is like a coin flip, but the coin doesn’t have to be fair. You’re not just saying “heads or tails”—you’re quantifying how biased your coin is. This plays directly into binary classification: will they churn or stay? Will the transaction be fraudulent or not?
2. Binomial Distribution
The Binomial distribution generalizes the Bernoulli trial to \(n\) repeated trials. It models the number of successes in a fixed number of independent experiments.
PMF: \(P(X = k) = \binom{n}{k} p^k (1 - p)^{n - k}\)
Let \(X \sim \text{Binomial}(n, p)\)
Then:
- Mean
We want: \(\mathbb{E}[X] = \sum_{k = 0}^n k \cdot \binom{n}{k} p^k (1 - p)^{n - k}\)
This sum is not easy to do directly. Instead, note:
A Binomial is the sum of \(n\) independent Bernoulli trials:
Let: \(X = \sum_{i=1}^n X_i \quad \text{where } X_i \sim \text{Bernoulli}(p)\)
Then:
\[\mathbb{E}[X] = \mathbb{E}\left[\sum_{i=1}^n X_i\right] = \sum_{i=1}^n \mathbb{E}[X_i] = \sum_{i=1}^n p = np\]- Variance
Use: \(\text{Var}(X) = \text{Var}\left(\sum_{i=1}^n X_i\right)\)
If the \(X_i\) are independent:
\[\text{Var}(X) = \sum_{i=1}^n \text{Var}(X_i) = \sum_{i=1}^n p(1 - p) = np(1 - p)\]Applications:
- Ensemble model success probability
- Simulating repeated trials
This plot below represents the probability of getting a certain number of successes in 10 independent trials, each with a 50% success rate. The binomial distribution models many real-world situations in machine learning, such as predicting how many models in an ensemble will make correct predictions. Notice how the distribution is symmetric when \(p = 0.5\) and peaks around \(n \cdot p = 5\).
from scipy.stats import binom
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
n, p = 10, 0.5
x = np.arange(0, n+1)
pmf = binom.pmf(x, n, p)
plt.bar(x, pmf)
plt.title(f"Binomial Distribution PMF (n={n}, p={p})")
plt.xlabel("Number of successes")
plt.ylabel("Probability")
plt.show()
Example: What’s the probability that exactly 3 out of 5 users click an ad, given \(p = 0.4\)?
This is:
\[P(X = 3) = \binom{5}{3} \cdot 0.4^3 \cdot (1 - 0.4)^2 \\ = 10 \cdot 0.064 \cdot 0.36 = 0.2304\]Let’s look at the entire PMF for \(n = 5\):
| k | \(P(X = k)\) |
|---|---|
| 0 | \(0.07776\) |
| 1 | \(0.2592\) |
| 2 | \(0.3456\) |
| 3 | \(0.2304\) |
| 4 | \(0.0768\) |
| 5 | \(0.01024\) |
Most of the probability mass lies around the mean (\(np = 2\)). It gives you a realistic way to model uncertain events in batches—think of ensemble classifiers, polling results, or test failures during a deployment.
3. Poisson Distribution
The Poisson distribution models the number of events that occur in a fixed interval of time or space, assuming the events occur independently and at a constant rate \(\lambda\).
PMF: \(P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!}\)
Let \(X \sim \text{Poisson}(\lambda)\)
This means:
- Mean
We want: \(\mathbb{E}[X] = \sum_{k=0}^\infty k \cdot \frac{\lambda^k e^{-\lambda}}{k!}\)
Let’s simplify it by shifting the index of the summation.
Note: when \(k = 0\), the term is zero (since \(0 \cdot \dots = 0\)), so we can write:
\[\mathbb{E}[X] = \sum_{k=1}^\infty k \cdot \frac{\lambda^k e^{-\lambda}}{k!}\]Now use the identity: \(k \cdot \frac{\lambda^k}{k!} = \lambda \cdot \frac{\lambda^{k-1}}{(k - 1)!}\)
So: \(\mathbb{E}[X] = \lambda e^{-\lambda} \sum_{k=1}^\infty \frac{\lambda^{k - 1}}{(k - 1)!}\)
Change variable: let \(j = k - 1\). Then: \(\sum_{k=1}^\infty \frac{\lambda^{k - 1}}{(k - 1)!} = \sum_{j=0}^\infty \frac{\lambda^j}{j!} = e^{\lambda}\)
So: \(\mathbb{E}[X] = \lambda e^{-\lambda} \cdot e^{\lambda} = \lambda\)
- Variance
We use: \(\text{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2\)
We already know \(\mathbb{E}[X] = \lambda\).
Let’s compute \(\mathbb{E}[X^2]\) using the identity: \(\mathbb{E}[X^2] = \mathbb{E}[X(X - 1)] + \mathbb{E}[X]\)
Let’s compute the first part: \(\mathbb{E}[X(X - 1)] = \sum_{k=0}^\infty k(k - 1) \cdot \frac{\lambda^k e^{-\lambda}}{k!}\)
Again, when \(k = 0\) or \(k = 1\), the term is zero, so:
\[\mathbb{E}[X(X - 1)] = \sum_{k=2}^\infty \frac{k(k - 1)\lambda^k e^{-\lambda}}{k!}\]Use: \(k(k - 1) \cdot \frac{\lambda^k}{k!} = \lambda^2 \cdot \frac{\lambda^{k - 2}}{(k - 2)!}\)
So: \(\mathbb{E}[X(X - 1)] = \lambda^2 e^{-\lambda} \sum_{k=2}^\infty \frac{\lambda^{k - 2}}{(k - 2)!} = \lambda^2\)
Therefore: \(\mathbb{E}[X^2] = \lambda^2 + \lambda\)
Finally: \(\text{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 = (\lambda^2 + \lambda) - \lambda^2 = \lambda\)
Applications:
- Anomaly detection (e.g., fraud or system failures)
- Modeling event frequency (web traffic, queueing)
from scipy.stats import poisson
lmbda = 4
x = np.arange(0, 15)
pmf = poisson.pmf(x, lmbda)
plt.bar(x, pmf)
plt.title(f"Poisson Distribution (λ={lmbda})")
plt.xlabel("k (events)")
plt.ylabel("Probability")
plt.show()
The Poisson distribution is commonly used for modeling the number of times an event occurs in a fixed interval. In the plot below, we use \(\lambda = 4\) to show the probability distribution of event counts. This distribution is especially useful in anomaly detection — for example, identifying if the number of failed login attempts is abnormally high.
The Poisson distribution models the number of times an event occurs in a fixed window — like how many calls hit a support line in an hour, or how many fraud alerts trigger in a minute.
As you increase \(\lambda\), the average number of events rises. The shape responds accordingly:
- For small \(\lambda\) (like 1 or 2), the distribution is tightly packed near zero — most time intervals contain few or no events.
- As \(\lambda\) increases, the curve shifts right and spreads out. It starts to resemble a bell curve, even though it’s technically discrete.
- This transition is a visual cue for the Law of Rare Events: a Poisson with large \(\lambda\) behaves like a normal distribution.
Imagine modeling failed login attempts. A low \(\lambda\) might indicate a healthy baseline. But if it creeps up and the distribution spreads — that could be your anomaly detector quietly waving a red flag.
Example: Suppose a fraud detection system detects 4 false positives per hour on average. What’s the probability of detecting exactly 6 in an hour?
\[P(X = 6) = \frac{4^6 e^{-4}}{6!} \approx \frac{4096 \cdot 0.0183}{720} \approx 0.122\]Even though the expected value is 4, there’s still a decent chance we’ll see 5, 6, or even more. The Poisson distribution handles this kind of rare-but-not-impossible behavior elegantly—perfect for call center queues, error logging, or fraud alerts.
4. Categorical (Multinoulli) Distribution
For one‑hot outcomes over \(K\) classes with probability vector \(\mathbf p\),
\[P(X=k)=p_k,\qquad k\in\{1,\dots,K\}, \quad\sum_k p_k=1.\]The pmf can be compactly written \(\prod_{k=1}^{K} p_k^{\mathbb 1[X=k]}\).
Treat the indicator vector \(\mathbf Y=(\mathbb 1[X=1],\dots,\mathbb 1[X=K])\):
- Mean \(\mathbb E[Y_k]=p_k\)
- Covariance
\(\operatorname{Cov}(Y_i,Y_j)= \begin{cases} p_i(1-p_i), & i=j,\\[4pt] -p_ip_j, & i\ne j. \end{cases}\)
Note the negative off‑diagonals—if one class fires, the others must switch off.
Why we meet it daily
- Softmax layer – neural nets output \(p_k\) and the loss is \(-\log p_{y_{\text{true}}}\), i.e. Categorical cross‑entropy.
- Naïve Bayes text – each token type is a Categorical draw conditioned on topic or label.
- Hidden‑Markov emission for discrete observations (POS tags, DNA bases).
- Synthetic label noise – flip a true label by sampling a new one from a Categorical confusion matrix.
- Conjugate posterior with Dirichlet prior: if prior \(\text{Dir}(\boldsymbol\alpha)\) and you observe counts \(\mathbf c\), posterior is \(\text{Dir}(\boldsymbol\alpha+\mathbf c)\)—the algebra that powers Thompson sampling bandits.
Continuous Distributions
Continuous distributions represent variables that can take on any value within a range. They are essential in feature modeling, regression analysis, generative modeling, and more.
1. Uniform Distribution
This distribution assigns equal probability to all values in an interval $[a, b]$.
PDF: \(f(x) = \frac{1}{b - a}, \quad a \leq x \leq b\)
- Mean
We compute:
\[\mathbb{E}[X] = \int_a^b x \cdot \frac{1}{b - a} \, dx = \frac{1}{b - a} \cdot \left[\frac{x^2}{2}\right]_a^b = \frac{1}{b - a} \cdot \frac{b^2 - a^2}{2}\]Using the identity \(b^2 - a^2 = (b - a)(b + a)\):
\[\mathbb{E}[X] = \frac{a + b}{2}\]- Variance
First:
\[\mathbb{E}[X^2] = \int_a^b x^2 \cdot \frac{1}{b - a} \, dx = \frac{1}{b - a} \cdot \left[\frac{x^3}{3}\right]_a^b = \frac{b^3 - a^3}{3(b - a)}\]Using \(b^3 - a^3 = (b - a)(b^2 + ab + a^2)\):
\[\mathbb{E}[X^2] = \frac{b^2 + ab + a^2}{3}\]Now subtract:
\[\text{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 = \frac{b^2 + ab + a^2}{3} - \left(\frac{a + b}{2}\right)^2\]Simplifying gives:
\[\boxed{\text{Var}(X) = \frac{(b - a)^2}{12}}\]Applications:
- Random initialization (e.g., neural network weights)
- Data simulation and control baselines
samples = np.random.uniform(0, 1, 10000)
sns.histplot(samples, bins=30, kde=True)
plt.title("Uniform Distribution [0,1]")
plt.show()
A uniform distribution is what pure “ignorance” looks like in probability — no value is more likely than another. This histogram reflects that: the bars are roughly equal height, showing that numbers in ([0, 1]) appear with almost equal frequency. Useful in simulations, noise generation, or when initializing without bias.
Example: Simulating customer spend between ₹500 and ₹1500.
- \[a = 500, b = 1500\]
- Any spend in this range is equally likely.
- \[\mathbb{E}[X] = \frac{a + b}{2} = 1000\]
- \[\text{Var}(X) = \frac{(b - a)^2}{12} = \frac{1000^2}{12} = 83,333.33\]
When you’re generating noise or doing random initialization (like weights in a neural network), the uniform distribution is your go-to. It says: “I know the range, but not the preference.”
2. Normal (Gaussian) Distribution
The Normal distribution is the most widely used distribution in statistics and machine learning, due to the Central Limit Theorem.
PDF: \(f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{- \frac{(x - \mu)^2}{2\sigma^2}}\)
Let \(X \sim \mathcal{N}(\mu, \sigma^2)\)
The PDF is: \(f(x) = \frac{1}{\sqrt{2\pi \sigma^2}} e^{- \frac{(x - \mu)^2}{2\sigma^2}}, \quad x \in (-\infty, \infty)\)
- Mean
Let’s compute: \(\mathbb{E}[X] = \int_{-\infty}^{\infty} x \cdot f(x) \, dx\)
Make a substitution:
Let \(z = \frac{x - \mu}{\sigma} \Rightarrow x = \mu + \sigma z, \quad dx = \sigma dz\)
Then the integral becomes: \(\mathbb{E}[X] = \int_{-\infty}^{\infty} (\mu + \sigma z) \cdot \frac{1}{\sqrt{2\pi}} e^{- \frac{z^2}{2}} dz\)
Break into two terms: \(\mu \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}} e^{-z^2/2} dz + \sigma \int_{-\infty}^{\infty} z \cdot \frac{1}{\sqrt{2\pi}} e^{-z^2/2} dz\)
The first integral is 1 (area under standard normal), the second is 0 (since it’s an odd function over symmetric interval).
So: \(\mathbb{E}[X] = \mu\)
- Variance
We compute: \(\text{Var}(X) = \mathbb{E}[X^2] - \mu^2\)
Start with: \(\mathbb{E}[X^2] = \int_{-\infty}^{\infty} x^2 \cdot f(x) dx\)
Using the same substitution: \(x = \mu + \sigma z \Rightarrow x^2 = \mu^2 + 2\mu\sigma z + \sigma^2 z^2\)
Then: \(\mathbb{E}[X^2] = \int_{-\infty}^{\infty} (\mu^2 + 2\mu\sigma z + \sigma^2 z^2) \cdot \frac{1}{\sqrt{2\pi}} e^{-z^2/2} dz\)
Split into three terms:
- \(\mu^2 \int e^{-z^2/2}\) ⇒ gives \(\mu^2\)
- \(2\mu\sigma \int z e^{-z^2/2}\) ⇒ zero (odd function)
- \(\sigma^2 \int z^2 e^{-z^2/2}\) ⇒ equals \(\sigma^2\)
So: \(\mathbb{E}[X^2] = \mu^2 + \sigma^2 \\ \Rightarrow \text{Var}(X) = \mu^2 + \sigma^2 - \mu^2 = \sigma^2\)
Applications:
- Linear regression assumptions
- PCA and feature decorrelation
- Modeling errors and noise
mu, sigma = 0, 1
samples = np.random.normal(mu, sigma, 10000)
sns.histplot(samples, bins=30, kde=True)
plt.title("Normal Distribution (μ=0, σ=1)")
plt.show()
The bell-shaped curve shown below represents the standard normal distribution. This is foundational to many algorithms in statistics and machine learning. It models noise, errors, and is used in methods like Principal Component Analysis (PCA). Thanks to the Central Limit Theorem, many sample-based statistics tend to follow this distribution even when the original data is not normal.
- Mean (μ) shifts the curve left or right. It’s the center — the most likely value.
- Standard deviation (σ) controls spread. Smaller σ = tall and narrow, larger σ = flat and wide.
As you adjust these sliders:
- Watch the peak move with μ. That’s your central tendency shifting.
- Stretch σ and you’ll see the tails fatten — this models greater uncertainty.
- Suppose the test scores of a model follow \(\mathcal{N}(75, 10^2)\).
What’s the probability a randomly selected model scores above 90?
Standardize:
\[Z = \frac{90 - 75}{10} = 1.5 \Rightarrow P(X > 90) = 1 - \Phi(1.5) \approx 0.0668\]Only ~6.7% of models score above 90. This kind of reasoning underpins everything from model evaluation to uncertainty bounds in predictions.
3. Student‑t Distribution
The \(t_\nu(\mu,\sigma)\) has heavier tails; perfect when outliers lurk.
\[f_{t}(x;\nu,\mu,\sigma)= \frac{\Gamma\!\bigl(\tfrac{\nu+1}{2}\bigr)} {\Gamma\!\bigl(\tfrac{\nu}{2}\bigr)\sqrt{\nu\pi}\,\sigma} \Bigl[1+\frac{1}{\nu}\Bigl(\frac{x-\mu}{\sigma}\Bigr)^{2}\Bigr]^{-\tfrac{\nu+1}{2}}.\]- Mean (exists for \(\nu>1\)): \(\mathbb E[X]=\mu\)
- Variance (exists for \(\nu>2\)): \(\operatorname{Var}(X)=\dfrac{\nu\sigma^{2}}{\nu-2}\)
Mixture view \(X\sim t_\nu(\mu,\sigma) \iff X=\mu+\sigma\,Z/\sqrt{V/\nu}\) where \(Z\sim\mathcal N(0,1)\) and \(V\sim\chi^2_\nu\). This scale‑mixture explains the fat tails: occasionally \(V\) is tiny, inflating variance.
import seaborn as sns, scipy.stats as st
grid = np.linspace(-8,8,400)
for nu in [3,10,30]:
sns.lineplot(x=grid, y=st.t.pdf(grid, df=nu), label=f"ν={nu}")
sns.lineplot(x=grid, y=st.norm.pdf(grid), label='Normal'); plt.show()
Data‑science applications
- Robust regression residuals – replacing \(\mathcal N\) with \(t_\nu\) down‑weights outliers via the mixture representation (EM updates the hidden \(\nu\)‑scaled precisions).
- Finance – daily returns fit a \(t\): fatter tails give more realistic VaR/ES risk.
- Bayesian – a Normal likelihood with unknown variance & Inv‑Gamma prior marginalises to Student‑t, making \(t\) the default predictive distribution when you’re uncertain about \(\sigma^2\).
4. Log‑Normal Distribution
If \(\ln X\sim\mathcal N(\mu,\sigma^{2})\) then \(X\) is log‑normal:
\[f_{\text{LN}}(x;\mu,\sigma)= \frac{1}{x\sigma\sqrt{2\pi}} \exp\!\Bigl[-\frac{(\ln x-\mu)^{2}}{2\sigma^{2}}\Bigr],\qquad x>0.\]- Mean \(\mathbb E[X]=e^{\mu+\tfrac12\sigma^{2}}\)
- Variance \(\operatorname{Var}(X)=\bigl(e^{\sigma^{2}}-1\bigr)\,e^{2\mu+\sigma^{2}}\)
Derivation uses moment‑generating function of the underlying Normal:
\(\mathbb E[e^{t\ln X}]=\exp\!\bigl(t\mu+\tfrac12 t^{2}\sigma^{2}\bigr).\) Plug \(t=1,2\), then subtract squared mean.
Used for:
- Session length & dwell‑time modelling in UX analytics.
- Geometric Brownian Motion step in Black–Scholes; option‑pricing engines simulate \(\log S_t\) with Normal increments.
- Noise in positive‑only sensors (e.g. lidar intensity).
Moment‑Generating Function (MGF)
The Core Idea:
The moment‑generating function wraps every raw moment of a random variable into a single, elegant formula:
Differentiate \(n\) times and plug in \(t=0\), and you instantly get the n‑th moment \(\mathbb{E}[X^{\,n}]\).
A Quick Example:
For a normal variable \(Y\sim\mathcal N(\mu,\sigma^{2})\) we have
Set \(t=1\) and you’ve computed \(\mathbb{E}[e^{Y}]\) in one line. That single evaluation is exactly what turns a normal in log‑space into the familiar log‑normal mean
$$ \mathbb{E}[X]=e^{\mu+\tfrac12\sigma^{2}}. $$Why It Matters:
- Squeezes every moment \((\mu,\,\sigma^{2},\,\dots)\) into one function.
- Makes sums of independent variables easy:
if \(X\perp Y\), then \(M_{X+Y}(t)=M_X(t)\,M_Y(t)\). - Acts like a “fingerprint” — two distributions with the same MGF (in a neighborhood of 0) are the same distribution.
Think of It Like This:
- An MGF is a moment vending machine: insert a derivative order, out pops the moment.
- Set \(t\) to a specific value to price exotic expectations, e.g. \(\mathbb{E}[e^{sX}]\) in option pricing.
In Practice:
- Log‑Normal derivations: Lets you compute mean & variance in seconds.
- Central‑Limit proofs: MGFs show why sums converge to a normal.
- Tail bounds (Chernoff): Exponential moments bound probabilities via Markov’s inequality.
5. Exponential Distribution
The exponential distribution describes the time between events in a Poisson process.
PDF: \(f(x) = \lambda e^{-\lambda x}, \quad x \geq 0\)
Let \(X \sim \text{Exponential}(\lambda)\)
The PDF is: \(f(x) = \lambda e^{-\lambda x}, \quad x \geq 0\)
- Mean
We compute: \(\mathbb{E}[X] = \int_0^\infty x \cdot \lambda e^{-\lambda x} dx\)
Use integration by parts:
Let:
- \[u = x \Rightarrow du = dx\]
- \[dv = \lambda e^{-\lambda x} dx \Rightarrow v = -e^{-\lambda x}\]
Then: \(\mathbb{E}[X] = -x e^{-\lambda x} \Big|_0^\infty + \int_0^\infty e^{-\lambda x} dx\)
The first term evaluates to 0:
- As \(x \to \infty\), \(x e^{-\lambda x} \to 0\)
- At \(x = 0\), the term is 0
So: \(\mathbb{E}[X] = \int_0^\infty e^{-\lambda x} dx = \left[-\frac{1}{\lambda} e^{-\lambda x} \right]_0^\infty = \frac{1}{\lambda}\)
- Variance
We need \(\mathbb{E}[X^2]\):
\[\mathbb{E}[X^2] = \int_0^\infty x^2 \cdot \lambda e^{-\lambda x} dx\]This is a known integral: \(\int_0^\infty x^2 \lambda e^{-\lambda x} dx = \frac{2}{\lambda^2}\)
So: \(\text{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2 = \frac{2}{\lambda^2} - \left(\frac{1}{\lambda}\right)^2 = \frac{1}{\lambda^2}\)
Applications:
- Survival and reliability analysis
- Modeling waiting times
lmbda = 1
samples = np.random.exponential(1/lmbda, 10000)
sns.histplot(samples, bins=30, kde=True)
plt.title("Exponential Distribution")
plt.show()
This plot shows the exponential distribution, which is often used to model the time between events in a Poisson process. It’s especially useful in survival analysis and reliability engineering. The curve declines rapidly, showing that events are most likely to happen shortly after the last one, and become less likely over time.
Say the average time between fraud alerts is 10 minutes ⇒ \(\lambda = \frac{1}{10}\).
- What’s the probability the next alert comes within 5 minutes?
This distribution is memoryless. Whether it’s been 1 minute or 100, the chance the event occurs next minute is still the same. Great for modeling time to failure, or how soon a customer will churn.
6. Beta Distribution
A flexible distribution on the interval [0,1], defined by two shape parameters \(\alpha\) and \(\beta\).
PDF: \(f(x; \alpha, \beta) = \frac{x^{\alpha-1}(1-x)^{\beta-1}}{B(\alpha, \beta)}\)
Let \(X \sim \text{Beta}(\alpha, \beta)\)
The PDF is: \(f(x) = \frac{1}{B(\alpha, \beta)} x^{\alpha - 1} (1 - x)^{\beta - 1}, \quad 0 < x < 1\)
Where: \(B(\alpha, \beta) = \frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha + \beta)}\)
- Mean
We compute: \(\mathbb{E}[X] = \int_0^1 x \cdot f(x) dx = \frac{1}{B(\alpha, \beta)} \int_0^1 x^\alpha (1 - x)^{\beta - 1} dx\)
This is the definition of the Beta function: \(B(\alpha + 1, \beta) = \int_0^1 x^{\alpha} (1 - x)^{\beta - 1} dx\)
So: \(\mathbb{E}[X] = \frac{B(\alpha + 1, \beta)}{B(\alpha, \beta)} = \frac{\Gamma(\alpha + 1)\Gamma(\beta)}{\Gamma(\alpha + \beta + 1)} \cdot \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}\)
Using \(\Gamma(\alpha + 1) = \alpha \Gamma(\alpha)\):
\[\mathbb{E}[X] = \frac{\alpha}{\alpha + \beta}\]- Variance
We now compute: \(\text{Var}(X) = \mathbb{E}[X^2] - (\mathbb{E}[X])^2\)
Again using the Beta function: \(\mathbb{E}[X^2] = \frac{1}{B(\alpha, \beta)} \int_0^1 x^{\alpha + 1}(1 - x)^{\beta - 1} dx = \frac{B(\alpha + 2, \beta)}{B(\alpha, \beta)}\)
Using identities:
- \[\Gamma(\alpha + 2) = (\alpha + 1)\alpha \Gamma(\alpha)\]
- \[\Gamma(\alpha + \beta + 2) = (\alpha + \beta + 1)(\alpha + \beta) \Gamma(\alpha + \beta)\]
After simplification: \(\mathbb{E}[X^2] = \frac{\alpha(\alpha + 1)}{(\alpha + \beta)(\alpha + \beta + 1)}\)
Now subtract square of mean: \(\text{Var}(X) = \frac{\alpha(\alpha + 1)}{(\alpha + \beta)(\alpha + \beta + 1)} - \left( \frac{\alpha}{\alpha + \beta} \right)^2 = \frac{\alpha \beta}{(\alpha + \beta)^2 (\alpha + \beta + 1)}\)
Applications:
- Bayesian modeling of probabilities
- Thompson sampling in reinforcement learning
from scipy.stats import beta
x = np.linspace(0, 1, 1000)
for a, b in [(2, 5), (5, 2), (2, 2)]:
plt.plot(x, beta.pdf(x, a, b), label=f"α={a}, β={b}")
plt.title("Beta Distributions")
plt.legend()
plt.show()
The Beta distribution is defined over the interval [0,1] and is commonly used to model probabilities themselves. In the visualization below, we use shape parameters \(\alpha = 2\) and \(\beta = 5\). This creates a distribution skewed toward 0, reflecting a belief that lower probability values are more likely. Beta distributions are essential in Bayesian statistics and exploration-exploitation algorithms like Thompson Sampling.
Let’s model uncertainty in a conversion rate estimate:
- We observed 2 successes, 8 failures ⇒ \(\alpha = 3, \beta = 9\) (with Laplace smoothing)
The Beta PDF will now reflect our belief that low conversion rates are more probable, but we still have uncertainty.
The Beta acts as a distribution over probabilities. It’s what makes Bayesian updating in Bernoulli processes possible. Thompson Sampling, A/B tests—all powered by this.
7. Gamma Distribution
A two-parameter generalization of the exponential distribution.
PDF: \(f(x) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha-1} e^{-\beta x}\)
Let \(X \sim \text{Gamma}(\alpha, \beta)\) where:
- \(\alpha\) is shape
- \(\beta\) is rate (not scale!)
The PDF is: \(f(x) = \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha - 1} e^{-\beta x}, \quad x > 0\)
- Mean
We use: \(\mathbb{E}[X] = \int_0^\infty x \cdot f(x) dx = \int_0^\infty x \cdot \frac{\beta^\alpha}{\Gamma(\alpha)} x^{\alpha - 1} e^{-\beta x} dx\)
Combine powers: \(= \frac{\beta^\alpha}{\Gamma(\alpha)} \int_0^\infty x^\alpha e^{-\beta x} dx\)
Make substitution: let \(u = \beta x \Rightarrow x = \frac{u}{\beta}, dx = \frac{du}{\beta}\)
Then: \(= \frac{\beta^\alpha}{\Gamma(\alpha)} \cdot \int_0^\infty \left(\frac{u}{\beta}\right)^\alpha e^{-u} \cdot \frac{1}{\beta} du \\ = \frac{\beta^\alpha}{\Gamma(\alpha)} \cdot \frac{1}{\beta^{\alpha + 1}} \int_0^\infty u^\alpha e^{-u} du\)
But: \(\int_0^\infty u^\alpha e^{-u} du = \Gamma(\alpha + 1)\)
And: \(\Gamma(\alpha + 1) = \alpha \Gamma(\alpha)\)
So: \(\mathbb{E}[X] = \frac{\alpha \Gamma(\alpha)}{\beta^{\alpha + 1}} \cdot \frac{\beta^\alpha}{\Gamma(\alpha)} = \frac{\alpha}{\beta}\)
- Variance
Same process, compute: \(\mathbb{E}[X^2] = \int_0^\infty x^2 f(x) dx = \frac{\beta^\alpha}{\Gamma(\alpha)} \int_0^\infty x^{\alpha + 1} e^{-\beta x} dx\)
Using the same substitution as above: \(\mathbb{E}[X^2] = \frac{\Gamma(\alpha + 2)}{\beta^2 \Gamma(\alpha)} = \frac{(\alpha + 1)\alpha \Gamma(\alpha)}{\beta^2 \Gamma(\alpha)} = \frac{\alpha(\alpha + 1)}{\beta^2}\)
Now subtract: \(\text{Var}(X) = \frac{\alpha(\alpha + 1)}{\beta^2} - \left( \frac{\alpha}{\beta} \right)^2 = \frac{\alpha}{\beta^2}\)
Applications:
- Waiting time models
- Priors in Bayesian inference
from scipy.stats import gamma
x = np.linspace(0, 20, 1000)
for shape in [1, 2, 5]:
plt.plot(x, gamma.pdf(x, shape), label=f"Shape={shape}")
plt.title("Gamma Distributions")
plt.legend()
plt.show()
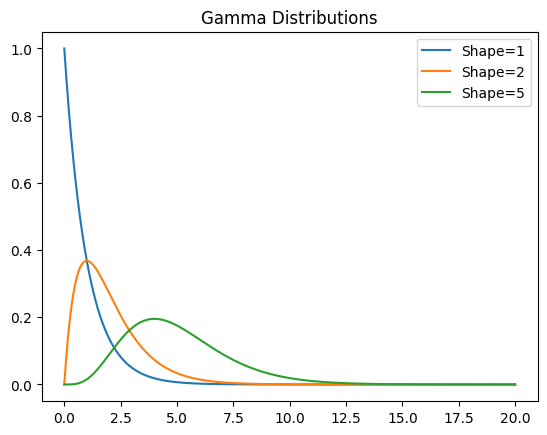
As you increase the shape parameter:
- When shape = 1, the distribution is identical to the exponential — memoryless and sharp.
- With shape = 2 or 5, the curve becomes more symmetric and shifted right — modeling delays that accumulate (e.g., time until 5 events occur).
- Suppose we’re modeling time to complete a task, and we know the average completion time is 5 units, with shape \(\alpha = 2\) ⇒ \(\beta = 0.4\).
Gamma lets you control both the shape and scale of your timing models. Used when you want exponential-like behavior but with more flexibility.
8. Chi-Square Distribution
The Chi-Square distribution is a special case of the gamma distribution with shape parameter \(k/2\) and scale \(\theta = 2\). It arises naturally when summing the squares of standard normal variables — hence its name.
Probability Density Function (PDF): \(f(x; k) = \frac{1}{2^{k/2} \Gamma(k/2)} x^{k/2 - 1} e^{-x/2}, \quad x \geq 0\)
Let \(X \sim \chi^2(k)\)
Chi-square is a special case of Gamma:
- \[\alpha = \frac{k}{2}\]
- \[\beta = \frac{1}{2}\]
So:
-
Mean: \(\mathbb{E}[X] = \frac{k}{2} \cdot \frac{1}{1/2} = k\)
-
Variance: \(\text{Var}(X) = \frac{k}{2} \cdot \frac{1}{(1/2)^2} = 2k\)
Applications:
- Hypothesis testing (e.g., Pearson’s chi-square test)
- Model goodness-of-fit
- Confidence intervals for variance
As degrees of freedom (df) increase, the distribution becomes more symmetric and bell-shaped — eventually approximating a normal distribution. With low df (e.g., 1 or 2), the distribution is highly skewed, with a sharp peak near zero. This makes the Chi-Square ideal for detecting unusual variation in small samples — like determining whether an observed data pattern could’ve arisen by chance.
Degrees of Freedom
The Core Idea:
Degrees of freedom (or df) just tells you how many values you’re free to choose in a calculation before the rest are locked in by a rule.
A Quick Example:
Imagine you have 3 numbers and you know their average must be 10.
That means the total must be:
$$ x_1 + x_2 + x_3 = 30 $$You can pick any two numbers freely — say 8 and 12. But the third one? It has no choice. It has to be 10 to keep the total at 30.
So even though there are 3 numbers, only 2 were truly “free” to vary.
That’s 2 degrees of freedom.
Why It Matters in Statistics:
- They adjust for how much of your data is already “used up” by model assumptions or estimates.
- If you've already calculated something like the mean, you have fewer pieces left to test with.
- The more you estimate, the fewer degrees of freedom remain.
Think of It Like This:
- Your data is like a puzzle.
- Every known total or constraint locks a piece into place.
- Degrees of freedom count how many pieces you can still freely choose.
In Practice:
- Chi-Square distributions: Degrees of freedom shape the curve.
- Regression models: They help track model complexity and prevent overfitting.
- T-tests: They determine how wide your confidence interval should be.
9. Dirichlet Distribution
Suppose a vector \(\mathbf P=(P_1,\dots,P_K)\) must live on the simplex \(\sum_k P_k=1,\;P_k\ge0\). The Dirichlet family places uncertainty on that whole vector.
\[f_{\text{Dir}}(\mathbf p;\boldsymbol\alpha)= \frac{1}{B(\boldsymbol\alpha)} \prod_{k=1}^{K} p_k^{\,\alpha_k-1},\qquad B(\boldsymbol\alpha)= \frac{\prod_k\Gamma(\alpha_k)}{\Gamma\!\bigl(\alpha_0\bigr)},\; \alpha_0=\sum_k\alpha_k.\]- Mean
\(\mathbb E[P_k]=\frac{\alpha_k}{\alpha_0}.\) - Variance
\(\operatorname{Var}(P_k)= \frac{\alpha_k(\alpha_0-\alpha_k)}{\alpha_0^{\,2}(\alpha_0+1)}.\) - Covariance (negative!)
\(\operatorname{Cov}(P_i,P_j)= -\frac{\alpha_i\alpha_j}{\alpha_0^{\,2}(\alpha_0+1)},\;i\ne j.\)
Why that formula? Take logs, recognise the Beta‑function normaliser \(B(\boldsymbol\alpha)\), and differentiate under the integral sign—textbook but illuminating.
Intuition of \(\alpha\)
- Large \(\alpha_0\) ⇒ vector concentrated near the mean; small \(<1\) ⇒ sparse “one class dominates”.
- \(\alpha=(1,1,\dots,1)\) ⇒ uniform over the simplex.
- In Bayesian parlance, \(\alpha_k-1\) acts like “pseudo‑count of class \(k\) before seeing data.”
import numpy as np, matplotlib.pyplot as plt
for a in [(0.5,0.5,0.5), (2,2,2), (5,1,1)]:
samp = np.random.dirichlet(a, size=500)
plt.scatter(samp[:,0], samp[:,1], alpha=0.3, label=str(a))
plt.legend(); plt.title("Dirichlet samples in 3‑simplex projection"); plt.show()
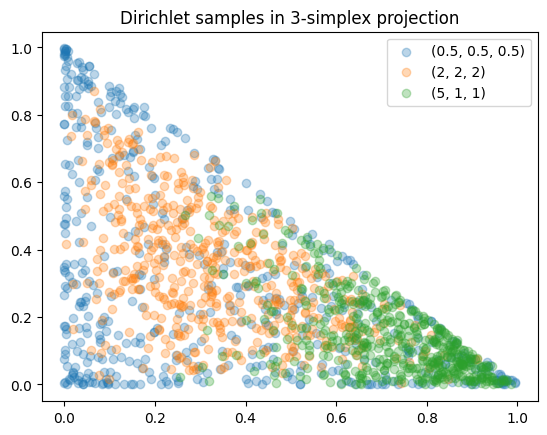
Data‑science uses
- CTR smoothing – posterior \(\text{Dir}(\alpha+\text{clicks})\) stabilises tiny sample sizes.
- Latent Dirichlet Allocation (LDA) – document‑topic vector \(\theta_d\sim\text{Dir}(\boldsymbol\alpha)\); topic‑word vector \(\phi_k\sim\text{Dir}(\boldsymbol\beta)\).
- Ensemble calibration – treat softmax outputs as draws from a Dirichlet and learn \(\boldsymbol\alpha\) to calibrate probabilities.
Multivariate Distributions
Multivariate distributions model joint behavior of multiple variables, especially when they are correlated.
0 Why We’re Leaving the Comfort of One Dimension
We meet probability through one random variable: roll a die, toss a coin, measure someone’s height.
But the data sets we actually wrangle are a choir of variables singing together.
Think of a customer:
-
tenurein months -
monthly_spendin dollars -
is_premium(0/1) -
avg_session_lengthin minutes
If churn prediction treats each column in isolation, we lose the harmony: customers who spend little and have been around only three months churn more often than either feature predicts alone.
Capturing that harmony is the job of multivariate distributions.
1 Joint Probability Distributions
1.1 Definition and Intuition
A joint distribution tells us how likely every possible pair \((x,y)\) is.
For discrete variables it’s a table; for continuous variables it’s a surface whose volume equals 1.
| Case | Name | Notation | Rules |
|---|---|---|---|
| Discrete | joint pmf | \(p_{X,Y}(x,y)\) | \(p_{X,Y}(x,y)\ge0\) and \(\sum_x\sum_y p_{X,Y}(x,y)=1\) |
| Continuous | joint pdf | \(f_{X,Y}(x,y)\) | \(f_{X,Y}(x,y)\ge0\) and \(\iint_{-\infty}^{\infty} f_{X,Y}(x,y)\,dx\,dy=1\) |
Mental picture Imagine a sandbox table at a science museum.
For a univariate pdf you pour sand along a line until the pile’s area is 1 —kids see a curve.
For a bivariate pdf you spread sand across a sheet; now the height varies over an \(x\)–\(y\) grid and the total volume is 1.
Different landscapes correspond to different correlations, skews, or clusters.
1.2 A Concrete Discrete Example
Below is an e‑commerce contingency table that records 1000 customers, whether they opened a campaign e‑mail (\(X\)), and whether they purchased within 24 hours (\(Y\)). Raw counts are on the left, cell‑wise probabilities on the right.
| \(X\) = opens? | \(Y\) = 0 (no purchase) | \(Y\) = 1 (purchase) | \(Y\) = 0 | \(Y\) = 1 | |
|---|---|---|---|---|---|
| 0 (didn’t open) | 420 | 80 | ⇒ | \(0.420\) | \(0.080\) |
| 1 (opened) | 320 | 180 | ⇒ | \(0.320\) | \(0.180\) |
| row totals | 740 | 260 | \(0.740\) | \(0.260\) |
The empirical joint pmf is
\[p_{X,Y}(x,y)=\frac{\text{count}(X=x,Y=y)}{1000}.\]Sanity check
\[\sum_{x,y}p_{X,Y}(x,y)=0.420+0.080+0.320+0.180=1.\]Marginals
- Open rate: \(P(X=1)=0.320+0.180=0.500\) (half the audience).
- Purchase rate: \(P(Y=1)=0.080+0.180=0.260\) (26 %).
Conditionals that matter to Marketing
Conversion among openers
\[P(Y=1\mid X=1)=\frac{0.180}{0.500}=0.360.\]Conversion among non‑openers
\[P(Y=1\mid X=0)=\frac{0.080}{0.500}=0.160.\]Openers are thus \(\tfrac{0.360}{0.160}\approx2.25\) times more likely to buy—solid evidence the subject line is doing real work.
Independence test (quick)
If \(X\) and \(Y\) were independent, we’d expect
\[p_{X,Y}(1,1)\stackrel{?}{=}P(X=1)P(Y=1)=0.500\times0.260=0.130.\]Observed is \(0.180\), far higher → clear dependence. A \(\chi^2\) test on the 2 × 2 table would reject independence with \(p\ll0.01\).
Covariance / correlation in the Bernoulli world
Treat \(X,Y\) as 0–1 indicators. Then
\[\operatorname{Cov}(X,Y)=\mathbb E[XY]-\mathbb E[X]\mathbb E[Y]=0.180-(0.500)(0.260)=0.050.\]Since \(\operatorname{Var}(X)=0.25\) and \(\operatorname{Var}(Y)=0.1924\),
\[\rho=\frac{0.050}{\sqrt{0.25\;\times\;0.1924}}\approx0.228.\]A modest positive correlation—exactly what the funnel story suggested.
How this tiny 2 × 2 feeds real data‑science
-
Naïve Bayes e‑mail scoring During training you collect tables like the one above for dozens of features (opened, clicked banner, device = mobile, etc.). Assuming conditional independence, the joint likelihood of a purchase becomes a simple product of the per‑feature conditionals \(P(\text{feature}\mid Y)\) estimated from such tables.
-
Lift / uplift modelling Marketing often asks “Will sending this e‑mail change purchase probability?” The difference \(0.360-0.160=0.200\) is precisely the uplift that uplift‑modelling algorithms try to predict across user segments.
-
AB‑testing power calculations You plug the baseline rate \(0.160\) and the detectable lift (say +0.04) into a power formula—ultimately derived from the variance of a Bernoulli—to decide how many users each variant must recruit.
-
Logistic‑regression feature encoding Binary \(X\) drops straight in as a predictor; its coefficient estimates \(\log\bigl(\tfrac{0.360}{0.160}\bigr)\approx0.816\), matching the odds ratio from the table.
So while the table looks tiny, the same arithmetic—counts → probabilities → marginals, conditionals, odds—is the backbone of large‑scale recommender systems, churn models, and advertising platforms.
1.3 A Continuous Superstar—the Bivariate Normal
Arguably the most important continuous joint distribution is the bivariate normal. It is the two‑dimensional cousin of the bell curve and sits at the core of Gaussian‑mixture clustering, Kalman filtering, PCA, linear‑Gaussian Bayesian networks, and the “kernel” of every Gaussian‑process regression.
The density is
\[f_{X,Y}(x,y)= \frac{1}{2\pi\,\sigma_X\sigma_Y\,\sqrt{1-\rho^{2}}}\, \exp\!\Bigl[ -\frac{1}{2(1-\rho^{2})} \Bigl( \Bigl(\frac{x-\mu_X}{\sigma_X}\Bigr)^{2} -2\rho\,\Bigl(\frac{x-\mu_X}{\sigma_X}\Bigr)\Bigl(\frac{y-\mu_Y}{\sigma_Y}\Bigr) +\Bigl(\frac{y-\mu_Y}{\sigma_Y}\Bigr)^{2} \Bigr) \Bigr].\]Parameter intuition
- \(\mu_X,\mu_Y\) shift the hill’s centre.
- \(\sigma_X,\sigma_Y\) control spread along the two axes.
- \(\rho\) (the Pearson correlation) tilts the hill into an ellipse.
- When \(\rho=0\) the exponential factorises, so \(X\) and \(Y\) are independent and the contours are perfect circles.
- As \(\rho\to1\) the hill collapses into an increasingly skinny diagonal cigar—knowing one coordinate almost pins down the other.
Linear‑algebra view Let \(\mathbf Z=[X\;Y]^\top\) with mean \(\boldsymbol\mu\) and covariance matrix
\[\Sigma= \begin{bmatrix} \sigma_X^{2} & \rho\sigma_X\sigma_Y\\ \rho\sigma_X\sigma_Y & \sigma_Y^{2} \end{bmatrix}.\]Then
\[f_{\mathbf Z}(\mathbf z)= \frac{1}{2\pi\sqrt{|\Sigma|}} \exp\!\bigl[-\tfrac12(\mathbf z-\boldsymbol\mu)^\top\Sigma^{-1}(\mathbf z-\boldsymbol\mu)\bigr].\]Because any linear transformation \(\mathbf A\mathbf Z+\mathbf b\) remains Gaussian—with mean \(\mathbf A\boldsymbol\mu+\mathbf b\) and covariance \(\mathbf A\Sigma\mathbf A^\top\)—linear models can push, rotate, and project Gaussians without leaving closed form. That property keeps Kalman‑filter updates analytic and lets PCA diagonalise \(\Sigma\) to find principal axes.
Think of the heat‑map as a living top‑down view of the bivariate‑normal “hill.” Each color band is a contour line—brighter means higher probability density. Drag the \(\rho\) slider and watch how two things happen at once:
-
Shape – for \(\rho = 0\) the contours are concentric circles, telling us \(X\) and \(Y\) wiggle independently. As \(\rho\) creeps toward \(\pm1\) those circles stretch into ever‑skinnier ellipses. Mathematically, you are watching the off‑diagonal term \(\rho\sigma_X\sigma_Y\) in the covariance matrix \(\Sigma\) push probability mass along the line \(y = (\rho\sigma_Y/\sigma_X)\,x\).
-
Orientation – positive \(\rho\) tilts the ridge up‑right (large \(X\) pairs with large \(Y\)); negative \(\rho\) flips it up‑left (large \(X\) with small \(Y\)). Hover over any pixel to see the exact pdf value and confirm that points on the ridge really are more likely.
Why care? If your real scatter plot matches one of the slider positions, you can read off the implied \(\rho\) by eye—a priceless intuition when eyeballing covariance structure before fitting PCA, Gaussian‑mixture clusters, or a Kalman filter. And if your data cloud looks nothing like any slider position (jagged tails, asymmetric blobs), that’s your cue that a plain Gaussian assumption is too naive and a heavier‑tailed model or copula is in order.
Analytic goodies you actually use
- Marginals stay normal: \(X\sim\mathcal N(\mu_X,\sigma_X^{2})\) and likewise for \(Y\).
-
Conditionals are normal:
\[X\mid Y=y\;\sim\;\mathcal N\!\Bigl( \mu_X+\rho\frac{\sigma_X}{\sigma_Y}(y-\mu_Y), (1-\rho^{2})\sigma_X^{2} \Bigr),\]the backbone of Gaussian‑process prediction and Kalman smoothing.
- Quadratic forms: for any weights \(a,b\), \(\mathbb E[(aX+bY)^{2}]=[a\;b]\,\Sigma\,[a\;b]^\top\)—the formula behind portfolio variance and signal‑to‑noise calculations.
Where it shows up in practice
- Gaussian Mixture Models: each cluster is a (possibly full‑covariance) multivariate normal; in two dimensions you literally fit overlapping bivariate Gaussians.
- Kalman/Particle filters: state prediction \(\mathbf x_{t+1}=A\mathbf x_t+\epsilon\) with \(\epsilon\sim\mathcal N(0,Q)\) preserves Gaussianity, so every pair of state dimensions is (at each step) a bivariate normal with an updated \(\Sigma_t\).
- PCA & whitening: diagonalising the empirical \(\widehat\Sigma\) (which reduces to the 2 × 2 case above when you keep two features) rotates the cloud to uncorrelated axes, then rescales to unit variance—essential for decorrelating inputs before feed‑forward nets.
- Copula diagnostics & asset pricing: if data look Gaussian after simple marginal transforms, plain \(\rho\) captures dependence nicely; if not, analysts reach for heavier‑tailed copulas.
- Simulated feature generation: need realistic synthetic data for robustness tests? Estimate \((\boldsymbol\mu,\Sigma)\), draw bivariate (or multivariate) normals, and pass them through inverse marginal CDFs.
Grasp this single distribution and you gain a master key: many “fancier” multivariate tricks are nothing more than clever ways to fit, transform, or stack bivariate normals.
2 Marginal Distributions – Solo Performances
A marginal answers the question “If I ignore the other variable, what does the distribution of the one I’m staring at look like?”
Formally
\[f_X(x)= \begin{cases} \displaystyle\sum_{y} p_{X,Y}(x,y), & \text{discrete},\\[8pt] \displaystyle\int_{-\infty}^{\infty} f_{X,Y}(x,y)\,dy, & \text{continuous}. \end{cases}\]In our email table
- \(P(X=1)=0.32+0.18=0.50\) → half the audience opens mails.
- \(P(Y=1)=0.08+0.18=0.26\) → 26 % purchase overall.
Why the name? Historically we wrote joint tables with \(x\) along rows, \(y\) across columns, and the margin contained row/column totals. The name stuck.
2.1 A Numeric Continuous Example
Take two continuous variables with pdf
\[f_{X,Y}(x,y)= \begin{cases} 2,& 0<y<x<1,\\ 0,&\text{otherwise}. \end{cases}\]Yes, that weird triangle integrates to 1 (check!).
The marginal of \(X\):
The marginal of \(Y\):
\[f_Y(y)=\int_{y}^{1} 2\,dx = 2(1-y),\quad 0<y<1.\]Beautiful symmetry—one rises linearly, the other falls.
3 Conditional Distributions – Slicing the Joint
When you know \(Y=y\), the “sand‑landscape” collapses into a vertical plane at that \(y\).
We must renormalise the slice, giving
For discrete pmfs just swap integrals for sums.
Example (email table)
\[P(Y=1\mid X=1)=\frac{0.18}{0.50}=0.36,\qquad P(Y=1\mid X=0)=\frac{0.08}{0.50}=0.16.\]Intuition Conditioning is “zoom and re‑scale.”
You restrict to the events compatible with \(Y=y\) and then stretch so the slice’s mass becomes 1.
4 Independence—When Roommates Ignore Each Other
Two variables are statistically independent iff their joint factorises:
\[f_{X,Y}(x,y)=f_X(x)\,f_Y(y)\quad\forall x,y.\]In plain English: knowing \(Y\) leaves your beliefs about \(X\) completely unchanged.
Checklist
- Discrete: \(p_{X,Y}(x,y)=p_X(x)\,p_Y(y).\)
- Continuous: \(f_{X,Y}(x,y)=f_X(x)\,f_Y(y).\)
Watch‑out Zero covariance (next section) doesn’t guarantee independence unless you’re normal. \(Y=X^2\) has \(\operatorname{Cov}(X,Y)=0\) but they’re obviously entangled.
5 Expectation Laws—Our Statistical Swiss Army Knife
5.1 The Law of Total Expectation
\[\boxed{\; \mathbb E[X]=\mathbb E\bigl[\mathbb E[X\mid Y]\bigr]\;}\]Proof (continuous)
\[\begin{aligned} \mathbb E[X] &=\iint x\,f_{X,Y}(x,y)\,dx\,dy \\[4pt] &=\int\Bigl[\int x\,\frac{f_{X,Y}(x,y)}{f_Y(y)}\,dx\Bigr]f_Y(y)\,dy \\[4pt] &=\int \mathbb E[X\mid Y=y]\,f_Y(y)\,dy. \end{aligned}\]Read right‑to‑left it says: take the conditional mean inside each vertical slice, weight by how probable the slice is, and you recover the grand mean.
5.2 The Law of Total Variance
\[\boxed{\; \operatorname{Var}(X)=\mathbb E[\operatorname{Var}(X\mid Y)] +\operatorname{Var}\!\bigl(\mathbb E[X\mid Y]\bigr)\;}\]Think of total variance as noise + explainable signal.
In regression you squeeze the second term (signal) from the first, hoping the unexplained noise is small.
5.3 Conditional Expectation by Example
Suppose \(Y\sim\text{Poisson}(\lambda)\) and, given \(Y=k\),
\(X\mid Y=k\sim\text{Binomial}(k,p)\).
This is a classic “number of successes in a random number of trials” hierarchy.
Compute \(\mathbb E[X]\) two ways.
(1) Direct
\[\mathbb E[X]=\mathbb E_Y[\mathbb E[X\mid Y]] =\sum_{k=0}^{\infty}\,\mathbb E[X\mid Y=k]\;P(Y=k) =\sum_{k=0}^{\infty} k\,p\,\frac{e^{-\lambda}\lambda^{k}}{k!} =p\,\lambda.\](2) Alternative
We can show \(X\) follows \(\text{Poisson}(p\lambda)\). The mean of a Poisson is its parameter → \(p\lambda\).
The agreement is comforting; the law of total expectation never lies.
6 Covariance & Correlation — Feeling the Sway in the Data
If variables were dancers, covariance tells us whether they lean in the same direction; correlation tells us how tightly they waltz.
We already met the formulas, but symbols alone rarely stick.
Let’s slow down, picture a few everyday scenes, and then crunch numbers to see the algebra turn into intuition.
6.1 What Covariance Feels Like
- Positive covariance
- Picture height and weight in a classroom.
Taller students tend to weigh more, so when one variable sits above its mean, the other is usually above its mean too.
Their product \((X-\mu_X)(Y-\mu_Y)\) is mostly positive → the average is positive.
- Picture height and weight in a classroom.
- Negative covariance
- Think of daily TV‑time vs grades (sadly).
More hours on Netflix often pair with lower grades.
Above‑mean TV time times below‑mean grades is negative; average that and you get a negative covariance.
- Think of daily TV‑time vs grades (sadly).
- Zero covariance
- Imagine shoe size and final‑exam date (fixed by the registrar).
They vary independently; products are just as often positive as negative → covariance near 0.
- Imagine shoe size and final‑exam date (fixed by the registrar).
Covariance carries units: \(\text{kg·cm}\), \(\text{dollars·hours}\), etc.
That’s why we invent correlation to strip units and pin the scale to \([-1,1]\).
6.2 Formal Definitions
- \(X, Y\) are two random variables (e.g., hours studied and exam scores).
- \(\mu_X = \mathbb{E}[X]\) is the mean (expected value) of \(X\).
- \(\mu_Y = \mathbb{E}[Y]\) is the mean of \(Y\).
- \(\mathbb{E}[XY]\) is the expected value of the product of \(X\) and \(Y\)—it reflects how the values move together.
- \(\operatorname{Cov}(X, Y)\) is the covariance, a measure of how much \(X\) and \(Y\) vary together.
Now here’s the key identity:
\[\operatorname{Cov}(X,Y)= \mathbb E[(X-\mu_X)(Y-\mu_Y)] =\mathbb E[XY]-\mu_X\,\mu_Y.\]Covariance captures the direction and strength of co-movement between two variables in their original units. It reflects whether larger values of one variable tend to occur with larger (or smaller) values of another, making it essential in formulas involving weighted combinations, such as portfolio risk or total variance.
Correlation is the normalized cousin:
\[\rho_{XY}= \frac{\operatorname{Cov}(X,Y)} {\sqrt{\operatorname{Var}(X)\operatorname{Var}(Y)}}.\]This standardized version of covariance is formally known as the Pearson correlation coefficient, denoted by \(\rho\). It measures the linear association between two variables on a unit-free scale, making it ideal for feature comparison, similarity metrics, and statistical inference.
More compact form
\[\begin{aligned} \operatorname{Cov}(X,Y) &=\mathbb E[(X-\mu_X)(Y-\mu_Y)]\\ &=\mathbb E[XY]-\mu_X\mu_Y \quad(\text{because }\mathbb E[X]=\mu_X,\; \mathbb E[Y]=\mu_Y). \end{aligned}\]That single line saves pages of algebra when you compute covariances in practice.
Covariance vs Correlation — intuition
| Concept | What you’re really doing | One tiny walk‑through | How to read the result |
|---|---|---|---|
| Covariance \(\displaystyle\operatorname{Cov}(X,Y)=\frac1n\sum_{i=1}^n (x_i-\bar x)(y_i-\bar y)\) | 1. Plot every \((x_i,y_i)\) dot. 2. Draw the two mean lines (vertical at \(\bar x\), horizontal at \(\bar y\)). 3. Each dot now sits in one of four quadrants: NE, NW, SE, SW. 4. Multiply its horizontal offset by its vertical offset. • NE & SW → product positive (they move together). • NW & SE → product negative (they move opposite). 5. Add every product and divide by \(n\). | Three students Hours–grades: \((2,70),(4,78),(6,86)\) Means: \(\bar x=4,\;\bar y=78\) Offsets: • (2–4)(70–78)=16 • (4–4)(78–78)=0 • (6–4)(86–78)=16 Sum = 32, divide by 3 → \(\operatorname{Cov}=10.7\) (positive). | Sign • positive → larger X tends to go with larger Y. • negative → larger X tends to go with smaller Y. • near‑zero → no consistent tilt. Units are mixed (here “hours × grade‑points”), so numbers from different problems are not directly comparable. |
| Correlation \(\displaystyle\rho_{XY}= \frac{\operatorname{Cov}(X,Y)}{\sigma_X\sigma_Y}\) | 1. Take the same cloud. 2. Shrink/stretch the x‑axis until its spread (SD) is 1; do the same to the y‑axis. 3. Repeat the covariance recipe. Because both axes are now on the same scale, the answer must sit between \(-1\) and \(+1\). | Same students again. Standard deviations: \(\sigma_X\approx1.63,\; \sigma_Y\approx6.53\). Rescaled covariance \(\rho\approx\frac{10.7}{(1.63)(6.53)}\approx0.78\). | Range \(-1\le\rho\le1\) \(\rho\approx1\) → dots lie on a rising line. \(\rho\approx0\) → no straight‑line pattern (they might still curve). \(\rho\approx-1\) → dots lie on a falling line. Unit‑free, so you can compare any two features from any data set. |
Green rectangles add positively to the sum; red (absent here) would subtract. After rescaling, the rectangles shrink but keep their sign, turning raw “hours × grade‑points” units into a unit‑free correlation on \([-1,1]\).
- Why the rectangle trick helps
- Visualising each \((X-\bar X)(Y-\bar Y)\) product as a little rectangle area makes covariance concrete: you literally add green (positive) and red (negative) tiles.
- Correlation just rescales the chessboard so one square in x‑direction equals one square in y‑direction; the tile colours stay the same, their sizes change.
- Take‑aways
- Look at the sign first. Positive and negative mean “move together” vs “move opposite.”
- Use correlation when you need a single, comparable score. Save covariance for formulas that require the actual units (e.g.\ portfolio variance \(w^\top\Sigma w\)).
- A small correlation does not guarantee independence. Non‑linear patterns (U‑shapes, circles) can fool it—always plot before you drop a feature.
Everyday analogies
-
Covariance as a see‑saw plank
Imagine \(X\) on the left support, \(Y\) on the right. Points in the NE or SW quadrants tilt the plank up, adding positive torque; points in NW or SE tilt it down, adding negative torque. The net torque is exactly the covariance. -
Correlation as choosing the radio station
Covariance gives you the raw electrical signal (voltage × amperage units). Turning the dial to “correlation” rescales the signal so every station’s loudness fits the same 0‑to‑1 volume bar—easy to compare, but you lose information about absolute power.
Rule‑of‑thumb guide
| If you want to… | Use | Because |
|---|---|---|
| Judge linear strength independent of scale | Correlation | \(\rho\) is bounded in \([-1,1]\), so \(0.6\) here equals \(0.6\) elsewhere. |
| Compute variance of a weighted sum \(Z=w_1X+w_2Y\) | Covariance | \(\operatorname{Var}(Z)=w_1^{2}\sigma_X^{2}+w_2^{2}\sigma_Y^{2}+2w_1w_2\operatorname{Cov}(X,Y)\). |
| Decide whether to drop a predictor in linear regression | Correlation | High absolute \(\rho\) with target → likely signal; near‑zero \(\rho\) may be noise (but check for curvature!). |
| Price portfolio risk or design hedges | Covariance matrix | Negative covariances reduce total variance—correlation alone can’t enter the quadratic form \(w^\top\Sigma w\). |
6.3 Numerical Walk‑Through
Below we compare two synthetic data sets built from clear mathematical recipes—no code needed.
| Case A – linear cigar | Case B – curved bowl | |
|---|---|---|
| Sample size | \(N = 3{,}000\) points | \(N = 3{,}000\) points |
| Input \(X\) | \(X_i \sim \mathcal N(0,1)\) | \(X_i = -3 + 6\frac{i}{N-1}\quad(i=0,\dots,N-1)\) |
| Noise \(\varepsilon\) | \(\varepsilon_i \sim \mathcal N\!\bigl(0,\;0.4^{2}\bigr)\) | \(\varepsilon_i \sim \mathcal N\!\bigl(0,\;0.5^{2}\bigr)\) |
| Output rule | \(Y_i = 0.8\,X_i + \varepsilon_i\) | \(Y_i = X_i^{2} + \varepsilon_i\) |
| Empirical covariance | \(\widehat{\operatorname{Cov}} \approx 0.65\) | \(\widehat{\operatorname{Cov}} \approx 0\) |
| Empirical Pearson \(\rho\) | \(\widehat\rho \approx 0.80\) | \(\widehat\rho \approx 0\) |
| Visual cue | elongated cigar slanting up‑right | symmetric U‑shape |
Zooming in on the geometry
Case A – the slanted cigar
Picture sprinkling dust along the straight line \(Y = 0.8X\) and nudging each speck sideways with independent Gaussian noise of standard deviation \(0.4\). When \(X\) is above its mean, \(Y\) is usually above its mean too, so the signed rectangles \((X-\overline X)(Y-\overline Y)\) are mostly positive. Stacking all \(3\,000\) rectangles yields a net positive area—covariance \(\approx 0.65\). After normalising by each variable’s spread (division by \(\sigma_X\sigma_Y\)) the area becomes a cosine: \(\rho \approx 0.80\).
Case B – the symmetric bowl
Now pour dust on the parabola \(Y = X^2\) and jiggle it vertically by Gaussian noise \(\sigma = 0.5\). For every point at \((x,y)\) on the right arm there is a mirror twin at \((-x,y)\) on the left. Their horizontal displacements have opposite signs, so the rectangle areas cancel pair‑wise. The grand total is essentially zero—hence covariance \(0\) and Pearson \(\rho = 0\)—despite the deterministic non‑linear link \(Y=X^2\).
Why we trip here
Pearson’s \(\rho\) measures linear association only.
- In Case A the linear fit \(\hat Y = 0.8X\) explains about \(\rho^{2} \approx 0.64\) of \(Y\)’s variance—residuals look like random fuzz.
- In Case B the best‑fit line is virtually flat; residuals trace a smile. If you relied on \(\rho=0\) alone you might wrongly throw \(X\) away.
Variance‑decomposition lens
\[\operatorname{Var}(Y) \;=\; \underbrace{\operatorname{Var}\!\bigl(\mathbb E[Y\mid X]\bigr)}_{\text{explainable signal}} \;+\; \underbrace{\mathbb E\!\bigl[\operatorname{Var}(Y\mid X)\bigr]}_{\text{irreducible noise}}.\]- Case A: \(\mathbb E[Y\mid X]=0.8X\) is linear ⇒ the “signal” term is large and visible to Pearson.
- Case B: \(\mathbb E[Y\mid X]=X^{2}\) is quadratic ⇒ a linear lens declares the signal invisible, misclassifying it as noise.
Practical playbook
- Plot first. Scatter plots uncover curvature, heteroscedasticity, clusters, outliers.
- If \(\rho\approx0\) but patterns remain, test rank‑based Spearman \(\rho_s\) or distance correlation—both flag Case B as dependent.
- Feature‑engineer or switch models. Adding \(X^{2}\) restores linearity; tree ensembles or Gaussian‑process kernels capture the shape automatically.
- Remember Pearson is brittle. A single extreme point can inflate or deflate \(\rho\); heavy‑tailed noise widens its sampling error.
| Scenario | Covariance | Correlation | Visual cue |
|---|---|---|---|
| A (linear) | \(\approx 0.65\) | \(\approx 0.80\) | elongated cigar ascending right‑up |
| B (U‑shape) | \(\approx 0.00\) | \(\approx 0.00\) | symmetric parabola |
Take‑away Zero correlation does not imply independence—the U‑shape hides a deterministic bond that Pearson cannot see.
6.4 Geometry Behind the Numbers
Imagine every data point \((x_i, y_i)\) as a dot cloud.
- Covariance is the signed area of the rectangle made by projecting each dot onto the two mean‑centered axes.
Lots of dots in the top‑right & bottom‑left quadrants → positive area. - Correlation rescales those axes to unit length, so the shape’s aspect ratio alone decides the number.
Mathematically, if you treat the demeaned vectors \(\mathbf x, \mathbf y\) as points in \(\mathbb R^n\),
\[\rho_{XY} = \frac{\mathbf x\cdot\mathbf y}{\|\mathbf x\|\;\|\mathbf y\|},\]which is exactly the cosine of the angle between two vectors.
Correlation = 1 means they’re pointing the same direction; 0 means they’re orthogonal.
6.5 Properties
-
Scaling
\(\operatorname{Cov}(aX+b,\;cY+d)=ac\,\operatorname{Cov}(X,Y).\) Shifting doesn’t matter; scaling does. -
Variance of a Sum
\(\operatorname{Var}(X+Y) =\operatorname{Var}(X)+\operatorname{Var}(Y)+2\,\operatorname{Cov}(X,Y).\)
For \(n\) variables this generalises to \(w^\top\Sigma w\) (portfolio risk). -
Cauchy–Schwarz Bounds Correlation
\(|\rho|\le1\); equality only if \(Y=aX+b\) almost surely. -
Independence ⇒ Zero Covariance (but not vice‑versa, as Case B showed).
6.6 Data‑Science Snapshots
| Domain | What’s measured | Why covariance matters |
|---|---|---|
| Portfolio theory | Daily returns of Apple & Microsoft | Portfolio variance is \(w^\top\Sigma w\); negative covariances are precious—they buy diversification. |
| Recommender systems | User A’s rating vector vs User B’s | Cosine similarity (= correlation) drives nearest‑neighbour search. |
| NLP word embeddings | Context vectors “king” & “queen” | High positive dot product → words share neighborhoods. |
| Computer vision | RGB channels in an image patch | PCA uses the 3×3 covariance to find principal colour axes; one axis often captures lighting, another colour tint. |
6.7 Common Pitfalls & How to Dodge Them
-
Spurious correlation — Ice‑cream sales & shark attacks both rise in summer; temperature is the lurking third variable.
Fix: control for seasonality, or compute partial correlations. -
Heteroscedastic clouds — Same mean relation, but spread changes over \(X\).
Ordinary least squares assumes constant variance; try weighted regression. -
Outlier domination — One extreme point can flip \(\rho\).
Use robust alternatives (Spearman, Kendall) or winsorize.
6.8 A Quick Sanity‑Check Recipe
- Plot a scatter‑matrix (
pandas.plotting.scatter_matrix). - Look for cigar shapes (\(\rho\approx\pm1\)), circles (\(\rho\approx0\)), or exotic curves (\(\rho\) misleading).
- Compute Pearson \(\rho\); if \(\approx0\) but pattern looks curved, test distance correlation or fit a GAM.
- Decide whether your model must capture or ignore that dependence.
Bottom line: Covariance shows direction of sway; correlation shows tightness of the embrace.
Keep both in your toolkit, but always look at the dance floor (scatter plot) before trusting the numbers.
6.9 Common Pitfalls & Remedies
| Pitfall | Symptom | Fix |
|---|---|---|
| Assuming independence too eagerly | Model under‑fits; residuals show structure | Inspect covariance / mutual information; add interaction terms or copulas |
| Confusing uncorrelated with independent | Misses curved relationships (e.g. \(Y=X^2\)) | Visualise joint scatter, or compute distance correlation |
| Forgetting conditional variance | Over‑confident intervals | Use law of total variance to combine aleatoric + epistemic parts |
| Singular covariance matrices | PCA or multivariate normal log‑likelihood fails | Remove redundant features / add small ridge term (cov + \(\varepsilon I\)) |
7 Beyond 2D: Vectors, Matrices, and Tensors
Everything above scales neatly:
- Joint pdf → \(f_{\mathbf X}(\mathbf x)\) where \(\mathbf X\in\mathbb R^d\).
- Marginal of coordinate \(i\): integrate out the other \(d-1\) variables.
- Covariance generalises to a matrix \(\Sigma\) with entries \(\Sigma_{ij}=\operatorname{Cov}(X_i,X_j)\).
The Mahalanobis distance \(d(\mathbf x)=\sqrt{(\mathbf x-\boldsymbol\mu)^\top \Sigma^{-1}(\mathbf x-\boldsymbol\mu)}\) powers anomaly detection.
In practice, dimensionality explodes: a 200‑feature data set has a 200×200 covariance (40 k unique entries).
Shrinkage estimators and sparse graphical models help tame that beast.
Summary Table: Choosing the Right Distribution — Quick Cheat‑Sheet
| Family | Canonical Parameters | Typical Questions It Answers | Telltale Data Clues | Common DS Workloads |
|---|---|---|---|---|
| Bernoulli | \(p=P(X=1)\) | “Will the event occur or not?” | One‑shot 0/1 outcomes, no over‑dispersion | baseline conversion, click / no‑click labels, success flags in AB tests |
| Binomial | \(n\) trials, success‑prob \(p\) | “How many successes out of n attempts?” | Bounded count \(\in\{0,\dots,n\}\), variance \(<\) mean | ensemble‐vote counts, email opens per user, quality‑control defect counts |
| Poisson | rate \(\lambda\) | “How many rare events in a fixed window?” | Non‑negative integer counts; mean ≈ variance | anomaly spikes per hour, API hits per second, insurance claim frequency |
| Exponential | rate \(\lambda\) (or mean \(1/\lambda\)) | “How long until the next event?” | Right‑skewed positive times; memoryless | inter‑arrival gaps, server uptime modelling, simple survival curves |
| Gamma | shape \(k\), scale \(\theta\) | “How long until the k‑th event?” (Erlang) | Positive, skew varies with \(k\) | task‑duration priors, Bayesian variance components, rainfall totals |
| Normal (Gaussian) | mean \(\mu\), std \(\sigma\) | “What’s the typical noisy deviation?” | Symmetric mound; empirical mean≈median≈mode | residual errors, z‑scores, Kalman noise, Central‑Limit approximations |
| Beta | \(\alpha,\beta\) (pseudo‑counts) | “What’s the uncertainty in a probability?” | Support in \([0,1]\); flexible U‑/bell‑shapes | Bayesian CTR posteriors, classical Beta‑Binomial smoothing |
| Multivariate Normal | mean \(\boldsymbol\mu\), covariance \(\Sigma\) | “How do features co‑vary jointly?” | Elliptical clouds, linear combos Gaussian | PCA whitening, Gaussian Mixture Models, Kalman filters |
| Categorical (Multinoulli) | class‑probs \((p_1,\dots,p_K)\) | “Which of K classes occurs?” | Exactly one hot per trial | multi‑class labels, topic id for one document |
| Dirichlet | \(\boldsymbol\alpha\) | Distribution over categorical probs | Vector in simplex; prior counts | LDA topic proportions, Bayesian smoothing for \(p_k\) |
| Student‑t | df \(\nu\), \(\mu,\sigma\) | “Like Normal but with fat tails” | Outliers heavier than Gaussian | robust regression errors, VaR stress tests |
| Log‑Normal | \(\mu,\sigma\) of underlying log | “Multiplicative growth data” | Positive, right‑skew, log‐symmetry | income, session length, file sizes |
How to read this table
- Canonical Parameters — the minimal set that fully characterises the distribution.
- Telltale Data Clues — quick empirical signs (mean–variance relationship, support, skew) that point to a candidate family.
- Common DS Workloads — everyday problems where practitioners reach for that distribution in modelling, simulation, or Bayesian priors.
Use the table as a first‑pass diagnostic: plot your data, eyeball its support & dispersion, then reach for the row whose “clues” resonate.
Probability distributions are at the core of every model you build in machine learning. They guide how you generate, structure, and analyze data. Whether you are simulating features, modeling uncertainty, or decomposing variance in PCA, the right distribution makes all the difference.
In the next post, we’ll move into the world of Bayesian inference and learn how concepts like MLE, MAP, and priors shape our understanding of parameter estimation.