Statistical Inference (Sampling, Confidence Intervals & Hypothesis Testing)

Sampling & Resampling Techniques
Over- and Under-sampling Techniques
Confidence Intervals & Interval Estimation
Hypothesis Testing

In the years after India gained independence, the country faced a formidable challenge: how to plan for the needs of a vast, diverse, and largely agrarian population. The government needed to know how much food was being produced, where it was grown, and how to plan for future demands. But with over 300 million people scattered across thousands of villages, measuring everything directly was not just expensive—it was nearly impossible.

Enter Prasanta Chandra Mahalanobis, a statistician with a vision.

Rather than trying to measure every farm and count every grain, Mahalanobis asked a different question: What if we could learn about the whole by carefully studying a part?

Drawing inspiration from the design of experiments and the theory of sampling, Mahalanobis proposed a radical solution for the time: use scientifically selected samples of farms to estimate agricultural yield for the entire country. He designed what came to be known as the large-scale sample survey, a method rooted in the principles of statistical inference.

With limited tools and massive geographic diversity, Mahalanobis built teams that would travel across India, carefully selecting plots of land to measure. Using rigorous stratified sampling techniques, they collected data that could be projected with known margins of error to the entire population.

His approach wasn’t just efficient—it was accurate. In fact, the results from the sample surveys often outperformed full enumeration methods, which were prone to human error, logistical failure, and political interference.

Mahalanobis’s work laid the foundation for the Indian Statistical Institute, and his survey framework became a global template, later adopted by the UN, FAO, and national statistical systems across the world.

But more importantly, his work showed that inference is not second-best—it’s often the most reliable and responsible way to understand the world.

This blog begins in the spirit of Mahalanobis: with the idea that we don’t need all the data to make good decisions. What we need is the right data, a thoughtful design, and the tools to reason from evidence.

Because the essence of statistical inference isn’t about certainty—it’s about clarity. And clarity, more often than not, begins with a well-framed question.

In data science, every insight, every model, and every product decision ultimately boils down to one central question: “Can we trust what we see in the data?” Whether you’re optimizing a website via A/B testing, evaluating model performance, or making predictions about future events, the challenge is the same — separating signal from noise.

This blog dives into the heart of that challenge through the lens of statistical inference — the mathematical machinery that lets us make educated guesses from data, quantify uncertainty, and draw conclusions that generalize beyond the immediate sample.

Statistical inference is practically essential in the day-to-day life of a data scientist, especially when:

You only have access to a sample and need to infer truths about a larger population.
You’re working with imbalanced datasets in high-stakes domains like fraud detection or healthcare.
You’re interpreting A/B test results to decide which product feature to roll out next.
You’re reporting insights to non-technical stakeholders and need to express uncertainty with clarity and confidence.

We’ll walk through the mathematical and practical building blocks of inference: Sampling, Confidence Intervals, and Hypothesis Testing — beginning from how we get data, to how confident we are about our estimates, and finally to how we make decisions based on those estimates.

Before diving into confidence intervals and testing claims, we must first understand how to obtain and work with samples. That’s where we begin — sampling techniques. Especially in the age of big data and machine learning, how you sample data can make or break the reliability of your models.

Sampling & Resampling Techniques

Statistical inference relies on the assumption that we can make valid generalizations from samples to populations. But to do that correctly, our sampling method must be rigorous and unbiased.

Let’s walk through three foundational sampling techniques: Random Sampling, Stratified Sampling, and Bootstrap Sampling. Each serves different purposes in data science workflows.

Random Sampling

Random sampling is the simplest and most fundamental sampling technique. It means selecting data points from a population entirely at random, such that each observation has an equal probability of being included.

Mathematically, suppose the population is
\(P = \{x_1, x_2, ..., x_N\}\)

A random sample of size \(n\) is a subset
\(S = \{x_{i_1}, x_{i_2}, ..., x_{i_n}\}\)
where each element \(x_{i_j}\) is drawn independently and uniformly from \(P\).

Random sampling ensures:

Unbiased representation of the population.
Validity of statistical estimators (like mean, variance).
Simplicity in implementation and analysis.

It forms the backbone of most inferential techniques—if your sample isn’t random, your conclusions might be misleading.

Here’s a Python implementation using numpy:

import numpy as np
import matplotlib.pyplot as plt

# Simulate a population
population = np.random.normal(loc=100, scale=15, size=10000)

# Draw multiple random samples
samples = [np.random.choice(population, size=200, replace=False) for _ in range(50)]
sample_means = [np.mean(s) for s in samples]

# Plot sample means distribution
plt.figure(figsize=(8, 5))
plt.hist(sample_means, bins=15, color="skyblue", edgecolor="black")
plt.axvline(np.mean(population), color="red", linestyle="--", label="True Population Mean")
plt.title("Distribution of Sample Means from Random Sampling")
plt.xlabel("Sample Mean")
plt.ylabel("Frequency")
plt.legend()
plt.show()

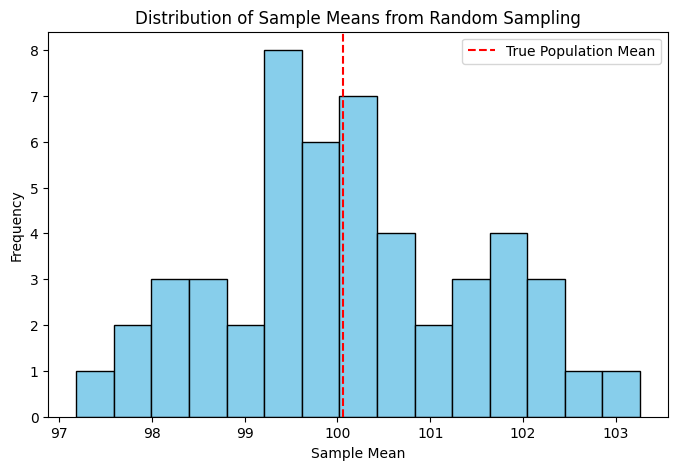
Figure: Distribution of Sample Means from Random Sampling

This histogram of sample means forms a bell-shaped curve around the population mean. Even though each sample is different, they center around the truth—a strong case for the power of randomness when done right.

Key inference: The sample mean should be close to the population mean if sampling is truly random.

Use it when:

The population is homogeneous.
You don’t need to preserve subgroup proportions.
You want a baseline unbiased estimate.

Applications

Random sampling is frequently used in:

Train-test splitting: When you want a quick, unbiased split of your dataset into training and testing sets, especially if no obvious subgroups exist.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

Baseline experiments: To evaluate a quick proof-of-concept model, especially before deploying stratification logic.
Hyperparameter tuning (cross-validation folds): Random folds are commonly used when there’s no class imbalance.
Data exploration: Subsampling large datasets (e.g., 100M+ rows) to make EDA faster.

While it’s simple, you must verify that the random sample reflects the population—especially if you’re publishing reports, building dashboards, or making business recommendations based on it.

Stratified Sampling

Stratified sampling is a method where the population is divided into strata (subgroups), and random samples are taken from each stratum proportionally.

Suppose a population is divided into \(K\) strata:
\(P = P_1 \cup P_2 \cup \cdots \cup P_K\)

Then a stratified sample is:
\(S = \bigcup_{k=1}^K \text{RandomSample}(P_k, n_k)\) where \(n_k\) is proportional to the size of stratum \(P_k\).

Sratified sampling:

Ensures representation of minority subgroups.
Reduces variance in estimates compared to simple random sampling.
Particularly useful when population is heterogeneous but within-stratum variance is low.

For instance, in a customer churn analysis, you’d want to ensure proper representation from each age group, or subscription tier.

import pandas as pd
from sklearn.model_selection import train_test_split

# Sample dataset with a categorical variable (strata)
data = pd.DataFrame({
    'customer_id': range(1, 101),
    'region': ['North']*25 + ['South']*25 + ['East']*25 + ['West']*25
})

# Stratified sampling based on 'region'
stratified_sample, _ = train_test_split(
    data, 
    test_size=0.8, 
    stratify=data['region'], 
    random_state=42
)

stratified_sample['region'].value_counts()

Below is a visualization where sampled dataset looks like a mini version of the population, at least in terms of region proportions. This kind of control is invaluable when fairness, accuracy, or subgroup insights matter.

import pandas as pd
import seaborn as sns
from sklearn.model_selection import train_test_split

# Simulate a dataset with four regions
df = pd.DataFrame({
    'customer_id': range(1, 1001),
    'region': np.random.choice(['North', 'South', 'East', 'West'], p=[0.1, 0.2, 0.3, 0.4], size=1000)
})

# Stratified sampling
stratified_sample, _ = train_test_split(df, test_size=0.9, stratify=df['region'], random_state=42)

# Plot distribution of regions before and after sampling
fig, axes = plt.subplots(1, 2, figsize=(12, 4))
sns.countplot(x='region', data=df, ax=axes[0])
axes[0].set_title("Region Distribution in Population")
sns.countplot(x='region', data=stratified_sample, ax=axes[1])
axes[1].set_title("Region Distribution in Stratified Sample")
plt.tight_layout()
plt.show()

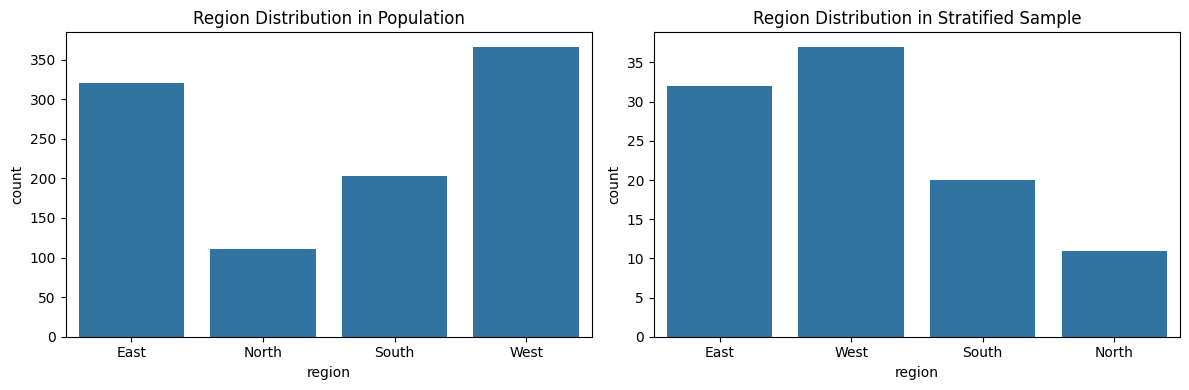
Distribution of regions before and after stratified sampling

Figure: Distribution of regions before and after sampling

Use it when:

There’s significant subgroup variation.
Ensuring fairness or balance is important (e.g., gender, geography).
Working on survey data, fraud detection, or churn modeling.

Applications

Stratified sampling is essential in situations where preserving the distribution of categorical variables is critical:

Classification with imbalanced classes: If a binary classification task has a 90:10 class imbalance, random sampling might draw mostly majority-class data. Stratified splits maintain label proportions in training and test sets.
```
train_test_split(X, y, stratify=y, test_size=0.2)
```
A/B testing: Ensuring equal representation of demographics (e.g., age, location) across control and treatment groups avoids bias in measured uplift.
Fairness auditing: When evaluating model fairness across race, gender, or geography, stratified resampling ensures all subgroups are well represented in evaluations.
Churn and fraud modeling: Helps in ensuring that underrepresented groups (like high-risk customers or low-frequency fraud cases) are adequately present in both training and evaluation datasets.

By reducing variance and improving subgroup coverage, stratified sampling leads to more stable model performance estimates, especially in regulated or high-stakes domains.

Bootstrap Sampling

Bootstrap sampling is a resampling method where we draw multiple samples with replacement from the original data to assess variability and confidence in our estimators.

Each bootstrap sample is of size \(n\), drawn from the original sample \(D\) of size \(n\), but with replacement.

Bootstrap Sampling:

Doesn’t require assumptions about the population distribution.
Useful for estimating confidence intervals, standard errors, or bias.
Central to ensemble learning methods (e.g., Bagging, Random Forests).

In Bootstrap Sampling, you repeatedly draw new samples with replacement from your original dataset and recompute your statistic each time. This generates an empirical distribution for your estimator, enabling things like confidence intervals—even when theoretical distributions don’t apply.

Let’s try this with the sample mean:

# Original dataset
data = np.random.exponential(scale=10, size=200)

# Generate bootstrap samples
boot_means = []
for _ in range(1000):
    sample = np.random.choice(data, size=len(data), replace=True)
    boot_means.append(np.mean(sample))

# Visualize bootstrap distribution
plt.figure(figsize=(8, 5))
sns.histplot(boot_means, bins=30, kde=True, color='salmon')
plt.axvline(np.mean(data), color='black', linestyle='--', label='Original Sample Mean')
plt.title("Bootstrap Distribution of Sample Mean")
plt.xlabel("Mean Value")
plt.ylabel("Density")
plt.legend()
plt.show()

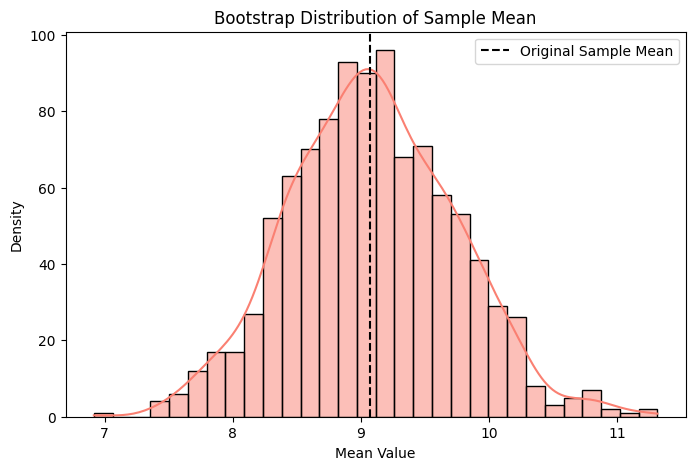
Figure: Bootstrap Distribution of Sample Mean

The curve you see is the distribution of possible means your sample could have yielded under small perturbations. The beauty here is that you don’t need to assume anything about the underlying population—it’s fully data-driven.

Bootstrap techniques are especially useful in model evaluation. For instance, if your test accuracy is 84%, a bootstrap confidence interval helps you say “I’m 95% confident that my true test accuracy lies between 82.5% and 85.5%,” even if the original test set was small or noisy.

Use it when:

You can’t assume normality or known variance.
You want empirical uncertainty bounds.
You’re working with small samples, complex models, or non-standard metrics.

Applications

Bootstrap sampling plays a central role in model evaluation, uncertainty estimation, and ensemble learning. Key areas include:

Estimating confidence intervals for:
- Accuracy, precision, recall, AUC, F1-score.
- Regression metrics like RMSE or R².
- Model coefficients in linear regression.
Stability analysis:
- How stable are your feature importances across different samples?
- Does your selected feature set generalize well?
Ensemble techniques:
- Bagging (Bootstrap Aggregating): Trains multiple models on bootstrapped samples and aggregates predictions.
```
from sklearn.ensemble import BaggingClassifier
clf = BaggingClassifier(base_estimator=..., n_estimators=10, bootstrap=True)
```
- Random Forests: Bootstrapped datasets + random feature subspaces.
- Model stacking: Bootstrap-based out-of-fold predictions used to train meta-models.
Model robustness checks:
- In high-stakes applications like medical diagnosis or fraud detection, bootstrapping helps quantify uncertainty without making strong distributional assumptions.
Time Series Bootstrapping (Block Bootstrapping):
- Helps maintain temporal structure when resampling sequence data.

When classical assumptions break down, bootstrap lets you fall back on the data itself to build empirical distributions. It’s one of the most versatile tools for modern data science.

Over- and Under-sampling Techniques

In many real-world data science problems, the data you work with isn’t evenly distributed. You might be dealing with an insurance dataset where fraudulent claims make up less than 1% of the total, or a healthcare dataset where only a small fraction of patients are diagnosed with a rare disease. These are classic examples of imbalanced datasets.

Training models on such data without addressing the imbalance often leads to biased predictions—where the model performs well on the majority class but poorly on the minority class, which is often the class of most interest.

To mitigate this, we rely on over- and under-sampling techniques. These methods adjust the class distribution in the training dataset to help models learn more effectively.

What Is Class Imbalance?

Formally, consider a binary classification task where the label variable is:

\[Y \in \{0, 1\}\]

A dataset is considered imbalanced if:

\[P(Y = 1) \ll P(Y = 0)\]

That is, one class (often called the minority class) has significantly fewer samples than the other (majority class). In such cases, standard learning algorithms tend to be biased toward predicting the majority class, often achieving high accuracy but low recall or F1 score for the minority.

Oversampling Techniques

Oversampling addresses imbalance by increasing the number of samples in the minority class. This can be done in several ways:

Random Oversampling

This is the simplest method—it duplicates random instances from the minority class until both classes are roughly equal in size. While easy to implement, this can lead to overfitting as the same examples are repeated multiple times.

When to use:

When you have very few examples of the minority class.
In small to medium-sized datasets where information loss would be costly.

Why:

It ensures the model has enough examples to learn the minority class.
Works well as a quick baseline.

SMOTE (Synthetic Minority Over-sampling Technique)

SMOTE is a more sophisticated approach that creates synthetic examples of the minority class rather than duplicating existing ones. The idea is to interpolate between an existing minority example and one of its k-nearest neighbors:

\[x_{\text{new}} = x_i + \lambda \cdot (x_{\text{nn}} - x_i)\]

Where:

\(x_i\) is a minority class sample
\(x_{\text{nn}}\) is one of its nearest neighbors in the same class
\[\lambda \sim \mathcal{U}(0, 1)\]

This way, SMOTE synthesizes new data points that lie along the line segment between pairs of minority points, enriching the minority space and encouraging the classifier to generalize better.

When to use:

When the minority class is clustered and has clear local structure.
When your model underfits the minority class or struggles with recall.

Why:

SMOTE helps balance the dataset by enriching the decision boundary around minority clusters.
It reduces overfitting and gives the model more generalizable signal from the minority class.

Advantages of SMOTE

Prevents overfitting by adding variability rather than duplicating.
Works well when minority samples are clustered.

Limitations of SMOTE

Can create overlapping between classes if used without care.
Assumes linear relationships between feature vectors.

ADASYN (Adaptive Synthetic Sampling)

ADASYN builds upon SMOTE by focusing on generating more synthetic samples in regions where the minority class is harder to learn (i.e., near decision boundaries). It adaptively determines the number of synthetic samples for each minority instance based on the local data distribution.

When to use:

When you suspect complex decision boundaries or sparse minority regions.
For tasks where recall is extremely critical (e.g., medical diagnosis).

Why:

By concentrating on difficult regions, ADASYN improves model sensitivity and encourages the model to learn more nuanced patterns.

This can improve model robustness in more complex regions but also increases the risk of introducing noise.

Visualizing SMOTE in Action

from imblearn.over_sampling import SMOTE
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt
import seaborn as sns

# Simulate an imbalanced dataset
X, y = make_classification(n_samples=1000, n_features=2, n_redundant=0,
                           n_clusters_per_class=1, weights=[0.9, 0.1],
                           class_sep=1.5, random_state=42)

# Apply SMOTE
smote = SMOTE(random_state=42)
X_resampled, y_resampled = smote.fit_resample(X, y)

# Plot
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
sns.scatterplot(x=X[:, 0], y=X[:, 1], hue=y, ax=axes[0], palette='Set1')
axes[0].set_title('Original Data')
sns.scatterplot(x=X_resampled[:, 0], y=X_resampled[:, 1], hue=y_resampled, ax=axes[1], palette='Set1')
axes[1].set_title('After SMOTE')
plt.tight_layout()
plt.show()

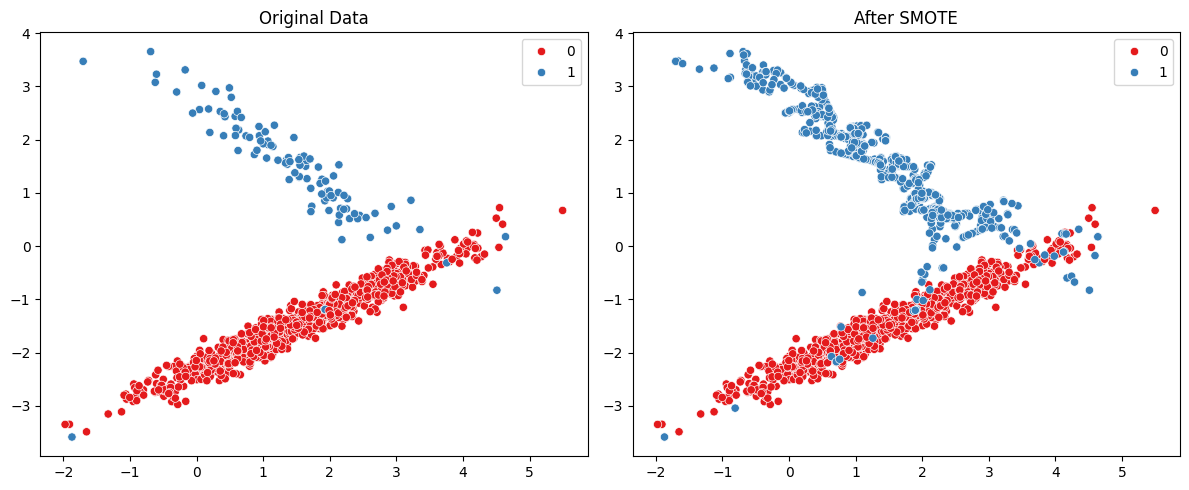
Figure: SMOTE in Action

Undersampling Techniques

Undersampling reduces imbalance by removing samples from the majority class. It is often used when the dataset is large enough that discarding data doesn’t hurt the learning process.

Random Undersampling

Removes random examples from the majority class. This method is fast but can lead to loss of important information if not carefully managed.

When to use:

When the dataset is large, and redundancy exists in the majority class.
When memory or training time is a concern.

Why:

Reduces training time and storage requirements.
Can serve as a quick fix for high imbalance when performance isn’t highly sensitive.

Tomek Links

Tomek Links aim to clean up borderline or noisy examples between classes. A pair \((x_i, x_j)\) is a Tomek Link if:

\(x_i\) and \(x_j\) are nearest neighbors
\(x_i\) belongs to the majority class, \(x_j\) to the minority

Removing \(x_i\) helps create a cleaner separation between classes.

When to use:

When decision boundaries are fuzzy or noisy.
As a post-processing step after oversampling (e.g., SMOTE).

Why:

Improves boundary definition and removes overlapping data.
Enhances class separability.

Edited Nearest Neighbors (ENN)

ENN removes any example whose class label disagrees with the majority of its k-nearest neighbors. This helps reduce class overlap and noise, especially near decision boundaries.

When to use:

When the dataset is noisy and overfitting is a concern.
For high-dimensional or sparse datasets where smoothing the boundary is necessary.

Why:

ENN enhances model generalization by removing borderline examples.
Improves signal clarity in classification tasks.

Hybrid Techniques

In practice, combining over- and under-sampling often yields the best results. For example:

SMOTE + Tomek Links: Add synthetic minority samples, then clean overlaps.
SMOTE + ENN: Generate new data, then remove noisy instances.

These hybrids combine the strengths of both approaches and are widely used in industry pipelines.

When to use:

When balancing precision and recall is critical.
When you’re aiming for high-quality decision boundaries without sacrificing generalization.

Why:

It mitigates weaknesses of individual techniques and improves end-to-end robustness.

Applications in Data Science

These resampling techniques are invaluable when dealing with:

Fraud Detection: Minority class represents fraud cases (« 1%).
Medical Diagnosis: Catching rare diseases early from unbalanced samples.
Churn Prediction: Churners are often a small minority.
Click-through Rate Prediction: Clicks are far less frequent than impressions.

In such domains, precision and recall are far more meaningful than accuracy.

Summary

Technique	Description	Best When
Random Oversampling	Duplicates minority class	Simple, quick baseline
SMOTE	Synthetic interpolation	Low sample, non-linear boundary
ADASYN	Synthetic + adaptive	Focus near decision boundaries
Random Undersampling	Drop majority class	Big data, low memory
Tomek Links	Clean overlaps	Remove borderline noise
ENN	Remove noisy points	Enhance decision boundary

To build models that are fair, robust, and interpretable, managing data imbalance with thoughtful sampling is not just a preprocessing step—it’s an integral part of model design.

Confidence Intervals & Interval Estimation

After understanding how we collect and rebalance our data, the next natural question is: how confident are we in the estimates derived from our samples? Whether it’s a mean conversion rate from an A/B test or a model accuracy score from evaluation data, point estimates tell only part of the story. We need a way to express uncertainty.

This is where Confidence Intervals (CIs) come in.

Confidence intervals are a statistical tool used to describe a range within which we believe a population parameter (such as the mean, proportion, or variance) lies, based on our sample data.

Rather than providing a single-point estimate (e.g., “conversion rate = 7.4%”), confidence intervals allow us to say:

“We are 95% confident that the true conversion rate lies between 6.8% and 8.0%.”

This idea of quantifying uncertainty is fundamental to statistical inference and deeply integrated into modern data science workflows.

Basics of Confidence Intervals

Let’s break it down from first principles.

What Is a Confidence Interval?

Formally, a confidence interval for a parameter \(\theta\) is constructed as:

\[[\hat{\theta} - E, \hat{\theta} + E]\]

Where:

\(\hat{\theta}\) is the estimate from the sample (e.g., sample mean, sample proportion)
\(E\) is the margin of error, which accounts for sampling variability

The margin of error depends on the standard error of the estimator and the desired confidence level.

The Meaning of a 95% Confidence Interval

Let’s say you construct a 95% confidence interval for the average time spent on a website.

What it means:

If you were to repeat the experiment 100 times and construct a CI each time, about 95 of those intervals would contain the true population mean.

What it doesn’t mean:

“There is a 95% probability that the true mean lies in this specific interval.”

This is a common misconception. Once the interval is constructed, it either contains the true value or it doesn’t. The 95% refers to the long-run frequency of intervals containing the truth.

Why Do Confidence Intervals Matter in Data Science?

Confidence intervals are used:

To quantify uncertainty in estimated model parameters (e.g., regression coefficients)
To compare versions in A/B tests without relying solely on p-values
To forecast and present prediction ranges (e.g., future demand, revenue)
To report model evaluation metrics (e.g., CI around F1-score or accuracy)

They make results more interpretable and trustworthy, especially when communicating with business stakeholders.

Constructing Confidence Intervals

Let’s now explore how to construct confidence intervals for different types of parameters.

For the Population Mean

The goal is to estimate the population mean \(\mu\) from a sample mean \(\bar{x}\) and to quantify our uncertainty about this estimate.

If the population standard deviation \(\sigma\) is known (rare in practice), and the sample size is sufficiently large, we use the Z-distribution:

\[\text{CI} = \bar{x} \pm z^* \cdot \frac{\sigma}{\sqrt{n}}\]

If the population standard deviation is unknown (common in real-world data), we use the sample standard deviation \(s\) and rely on the T-distribution:

\[\text{CI} = \bar{x} \pm t^* \cdot \frac{s}{\sqrt{n}}\]

Where:

\(\bar{x} = \frac{1}{n} \sum_{i=1}^n x_i\) is the sample mean
\(s = \sqrt{\frac{1}{n-1} \sum_{i=1}^n (x_i - \bar{x})^2}\) is the sample standard deviation
\(n\) is the sample size
\(z^*\) is the critical value from the standard normal distribution for the chosen confidence level
\(t^*\) is the critical value from the t-distribution with \(n - 1\) degrees of freedom

The term \(\frac{s}{\sqrt{n}}\) is known as the standard error of the mean (SEM). It reflects how much variation we’d expect if we repeated the sampling process.

For the Population Proportion

Suppose we are estimating the proportion \(p\) of a population having some binary attribute (e.g., users who clicked on an ad). Let \(\hat{p}\) be the sample proportion:

\[\hat{p} = \frac{x}{n}\]

Where:

\(x\) is the number of “successes” in the sample
\(n\) is the total number of observations

The standard error for the sample proportion is:

\[SE = \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}}\]

Then the CI becomes:

\[\text{CI} = \hat{p} \pm z^* \cdot SE = \hat{p} \pm z^* \cdot \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}}\]

This interval is valid under the normal approximation rule, typically when:

\[n \cdot \hat{p} \geq 5 \quad \text{and} \quad n \cdot (1 - \hat{p}) \geq 5\]

For the Population Variance or Standard Deviation

To estimate the population variance \(\sigma^2\), we use the chi-square distribution. The confidence interval for \(\sigma^2\) is given by:

\[\left[ \frac{(n - 1)s^2}{\chi^2_{\alpha/2}}, \frac{(n - 1)s^2}{\chi^2_{1 - \alpha/2}} \right]\]

Where:

\(s^2\) is the sample variance
\(n\) is the sample size
\(\chi^2_{\alpha/2}\) and \(\chi^2_{1 - \alpha/2}\) are critical values from the chi-square distribution with \(n - 1\) degrees of freedom

The CI for the population standard deviation \(\sigma\) is obtained by taking square roots:

\[\left[ \sqrt{\frac{(n - 1)s^2}{\chi^2_{\alpha/2}}}, \sqrt{\frac{(n - 1)s^2}{\chi^2_{1 - \alpha/2}}} \right]\]

These intervals are especially useful when you’re estimating the spread of a distribution—important in risk-sensitive applications such as financial volatility estimation or experimental measurements.

Using Z-distribution vs T-distribution

One of the most common questions in constructing confidence intervals for the mean is:

“Should I use the Z-distribution or the T-distribution?”

The answer depends on two factors: sample size and knowledge of population standard deviation (\(\sigma\)).

Z-distribution (Standard Normal)

Use when:

Sample size \(n \geq 30\) (large sample; Central Limit Theorem applies)
Population standard deviation \(\sigma\) is known

The formula becomes:

\[\text{CI} = \bar{x} \pm z^* \cdot \frac{\sigma}{\sqrt{n}}\]

T-distribution

Use when:

Sample size is small (\(n < 30\))
\(\sigma\) is unknown and estimated using sample standard deviation \(s\)

The formula becomes:

\[\text{CI} = \bar{x} \pm t^* \cdot \frac{s}{\sqrt{n}}\]

Why the Difference?

The T-distribution is wider and has heavier tails than the Z-distribution to account for the extra uncertainty introduced by estimating \(\sigma\) using \(s\). As the sample size increases, the T-distribution converges to the Z-distribution.

In practice:

In real-world data science, we usually don’t know \(\sigma\).
So, for small \(n\): use T.
For large \(n\): using Z is acceptable, even if \(\sigma\) is unknown, due to the Central Limit Theorem.

Summary table:

Scenario	Use Z	Use T
\(\sigma\) known & large \(n\)	✅	❌
\(\sigma\) known & small \(n\)	✅ (rare case)	❌
\(\sigma\) unknown & large \(n\)	✅ (approx)	✅ (better)
\(\sigma\) unknown & small \(n\)	❌	✅

Confidence Intervals in Practice

In real-world applications, confidence intervals are most impactful when they are used to support decisions, quantify uncertainty, or compare competing hypotheses. Let’s walk through two of the most common scenarios:

Confidence Intervals for the Difference of Means or Proportions

Suppose you’re testing two versions of a website: A and B. Your goal is to estimate the difference in average click-through rate (CTR) between them:

Let \(\mu_A\) and \(\mu_B\) represent the true average CTRs for versions A and B, respectively.

We define the difference:

\[\Delta = \mu_B - \mu_A\]

We estimate it using sample means:

\[\hat{\Delta} = \bar{x}_B - \bar{x}_A\]

The standard error of this difference is:

\[SE_{\hat{\Delta}} = \sqrt{\frac{s_A^2}{n_A} + \frac{s_B^2}{n_B}}\]

Assuming independent samples, the confidence interval becomes:

\[\hat{\Delta} \pm t^* \cdot SE_{\hat{\Delta}}\]

Where:

\(s_A^2\) and \(s_B^2\) are the sample variances for groups A and B
\(n_A\) and \(n_B\) are the sample sizes
\(t^*\) is the critical value from the t-distribution (based on approximate or pooled degrees of freedom)

This is widely used in A/B testing, where the estimated difference is not enough—you also need to know if that difference is statistically meaningful.

Similarly, for comparing proportions (e.g., proportion of users who clicked), the CI for the difference is:

\[\text{CI} = (\hat{p}_B - \hat{p}_A)\] \[\pm z^* \cdot \sqrt{\frac{\hat{p}_A (1 - \hat{p}_A)}{n_A} + \frac{\hat{p}_B (1 - \hat{p}_B)}{n_B}}\]

This is used in scenarios like:

Conversion rate comparisons
Click-through analysis
Response rate differences in surveys or experiments

Confidence Intervals for Regression Coefficients

In regression analysis, we often want to measure how confidently we can say that a predictor (feature) affects the outcome.

Let’s consider a simple linear regression:

\[Y = \beta_0 + \beta_1 X + \varepsilon\]

We estimate the slope \(\beta_1\) and intercept \(\beta_0\) from the sample.

The confidence interval for the slope \(\beta_1\) is given by:

\[\text{CI}_{\beta_1} = \hat{\beta}_1 \pm t^* \cdot SE_{\hat{\beta}_1}\]

Where:

\(\hat{\beta}_1\) is the estimated slope from the regression
\(SE_{\hat{\beta}_1}\) is the standard error of the slope estimate, derived from the residual variance and spread of \(X\)

The standard error is calculated as:

\[SE_{\hat{\beta}_1} = \sqrt{\frac{\hat{\sigma}^2}{\sum (x_i - \bar{x})^2}}\]

Where \(\hat{\sigma}^2\) is the residual mean squared error (MSE).

The confidence interval tells us:

If it contains zero, the predictor may not be significant.
If it’s narrow, we have high confidence in our estimate.
If it’s wide, more data or a better model may be needed.

These intervals are essential in:

Feature selection: Which variables are statistically significant?
Model interpretation: How much does a 1-unit change in \(X\) affect \(Y\)?
Business communication: Reporting confidence, not just coefficients.

Prediction Intervals vs. Confidence Intervals

While confidence intervals tell us how certain we are about the estimated mean response, prediction intervals go one step further: they capture the uncertainty in individual outcomes.

Let’s break down the distinction:

Confidence Interval (CI)

Used to quantify the uncertainty in the estimated average (mean) response \(\hat{y}\) for a given value of the predictor \(x\).

For a regression model:

\[\hat{y} = \hat{\beta}_0 + \hat{\beta}_1 x\]

The CI is:

\[\hat{y} \pm t^* \cdot SE_{\hat{y}}\]

Where:

\(SE_{\hat{y}}\) accounts for uncertainty in estimating the population mean at that \(x\)
The interval is narrower because it’s just about the mean

Prediction Interval (PI)

Used to quantify the uncertainty in a new individual outcome \(y_{\text{new}}\) at a given \(x\).

The PI is:

\[\hat{y} \pm t^* \cdot \sqrt{SE_{\hat{y}}^2 + \hat{\sigma}^2}\]

Here:

\(SE_{\hat{y}}^2\) is the uncertainty in estimating the mean
\(\hat{\sigma}^2\) is the estimated residual variance (inherent noise in the data)

This interval is always wider than a confidence interval because it must account for:

The uncertainty in the estimate and
The natural variation in outcomes even if the model is perfect

Summary

Interval Type	Captures uncertainty in…	Use case example
Confidence Interval	Estimated mean response \(\hat{y}\)	Average revenue per user forecast
Prediction Interval	Individual outcome \(y_{\text{new}}\)	Predicting next month’s exact revenue

Prediction intervals are especially valuable in forecasting problems:

Future sales or demand
Time series prediction intervals
Risk-sensitive decisions (e.g., confidence bounds on losses)

Bootstrap Confidence Intervals

In many practical settings, we don’t know the exact distribution of the data, or the assumptions required for parametric CIs (like normality or known variance) don’t hold. This is where bootstrap confidence intervals shine.

What Is the Bootstrap?

Bootstrap is a non-parametric resampling technique:

Repeatedly draw samples with replacement from the observed data
Recalculate the statistic of interest each time (mean, median, accuracy, etc.)
Use the distribution of these bootstrapped statistics to construct the CI

Let the original dataset be \(D = \{x_1, x_2, ..., x_n\}\). A bootstrap sample \(D^*\) is formed by sampling \(n\) observations from \(D\) with replacement.

Do this \(B\) times, compute statistic \(\theta^*_b\) on each sample, and construct an empirical distribution.

Types of Bootstrap Confidence Intervals

Let \(\{\theta_1^*, \theta_2^*, ..., \theta_B^*\}\) be the bootstrapped estimates.

Percentile Interval
- CI is the range between the \(\alpha/2\) and \(1 - \alpha/2\) quantiles: \([\theta^*_{\text{lower}}, \theta^*_{\text{upper}}]\)
- Intuitive and commonly used
Basic Bootstrap Interval
- Based on reflecting the bootstrap distribution around the original estimate: \([2\hat{\theta} - \theta^*_{(1 - \alpha/2)}, 2\hat{\theta} - \theta^*_{(\alpha/2)}]\)
- Attempts to correct bias
Bias-Corrected and Accelerated (BCa) Interval
- Adjusts for both bias and skewness in the bootstrap distribution
- More computationally intensive, but robust in practice

When and Why to Use Bootstrap CIs

When assumptions of parametric methods are violated
When estimating complex statistics (e.g., medians, regression coefficients, AUC)
When sample size is small and distributional form is unknown
In model evaluation: precision, recall, AUC, accuracy on test sets
In ensemble methods: confidence bands over aggregated predictions

Example: Constructing a 95% CI for test set accuracy:

Generate 1000 bootstrap test sets
Evaluate accuracy each time
Sort accuracies and take the 2.5th and 97.5th percentiles

This lets you say: “My model’s accuracy is 0.84, with a 95% CI between 0.81 and 0.87.”

Bootstrap brings the power of inference to complex or data-driven pipelines—without relying on strong assumptions.

Confidence Intervals in Model Evaluation

Evaluating a machine learning model requires more than reporting a single performance number like accuracy or F1-score. These numbers are estimates, and like all estimates from data, they come with uncertainty. Confidence intervals in model evaluation help quantify that uncertainty and give a range for how much our performance metrics might vary if we retrained or tested on different data.

Confidence Intervals for Accuracy Metrics

Let’s say you’ve trained a classification model and measured its performance on a test set. You report:

Accuracy = 86%
Precision = 72%
Recall = 67%
F1-score = 69%

But what if your test set was just one of many possible test samples? How would these scores change across different samples? Confidence intervals answer this.

Using bootstrapping (or analytical approximations), we can compute intervals for these metrics.

For accuracy, if your model made \(n\) predictions, and \(k\) were correct, then sample accuracy is:

\[\hat{p} = \frac{k}{n}\]

The standard error (SE) of accuracy is:

\[SE = \sqrt{\frac{\hat{p}(1 - \hat{p})}{n}}\]

Then a confidence interval is:

\[\hat{p} \pm z^* \cdot SE\]

This works well for large \(n\). For precision, recall, and F1-score (especially in imbalanced classification), bootstrap CIs are more appropriate because these metrics are nonlinear functions of counts.

Bootstrap-based evaluation:

Draw 1000 bootstrap samples from your test set.
Recompute precision, recall, F1 on each.
Use the empirical distribution to compute 95% CIs.

This approach lets you report model performance like:

F1-score = 0.69 [95% CI: 0.65, 0.73]

Now the audience knows the performance may vary by ±0.04 across different samples.

Confidence Intervals in Cross-Validation

Cross-validation (CV) is used to get a stable estimate of model performance, but results across folds still vary. Reporting a confidence interval helps reflect the variability across CV splits.

Let’s say you perform 10-fold CV and obtain 10 accuracy scores: \(a_1, a_2, ..., a_{10}\).

Compute mean accuracy: \(\bar{a} = \frac{1}{10} \sum_{i=1}^{10} a_i\)
Compute sample standard deviation \(s\): \(s = \sqrt{\frac{1}{9} \sum_{i=1}^{10} (a_i - \bar{a})^2}\)
Standard error: \(SE = \frac{s}{\sqrt{10}}\)
Confidence interval: \(\bar{a} \pm t^* \cdot SE\)

This allows you to report something like:

10-fold CV Accuracy: 0.862 [95% CI: 0.841, 0.883]

This range is especially useful when comparing models or tuning hyperparameters—if confidence intervals overlap, the differences may not be meaningful.

Confidence Intervals for Uplift or Lift in A/B/Uplift Modeling

In A/B tests or uplift modeling, the goal is often to measure the incremental effect of a treatment (e.g., showing a promotion, changing a UI).

Let:

\(p_T\) = conversion rate in treatment group
\(p_C\) = conversion rate in control group
\(\Delta = p_T - p_C\) = uplift or lift

We estimate this from sample proportions:

\[\hat{\Delta} = \hat{p}_T - \hat{p}_C\]

The standard error for the difference is:

\[SE = \sqrt{\frac{\hat{p}_T(1 - \hat{p}_T)}{n_T} + \frac{\hat{p}_C(1 - \hat{p}_C)}{n_C}}\]

The confidence interval for the uplift is:

\[\hat{\Delta} \pm z^* \cdot SE\]

Example:

Treatment conversion = 12%, Control conversion = 9%
Uplift = 3%
CI = [1.2%, 4.8%]

This tells us the lift is statistically significant and likely to be between 1.2% and 4.8% in the population.

Uplift models may go further by segmenting this estimate (e.g., uplift for high-value users vs low-value users). CIs for those subgroup effects are essential to:

Assess whether targeting is robust
Ensure fairness and reliability

Confidence intervals in model evaluation help quantify uncertainty and provide trustworthy boundaries for decision-making. They give practitioners and stakeholders a clearer sense of what’s known, what’s variable, and how decisions can be responsibly made.

Key Concepts in Confidence Intervals

To effectively use confidence intervals, it’s crucial to understand the foundational concepts that govern their behavior: margin of error, level of confidence, interval width, and the impact of sample size.

Margin of Error

The margin of error (MoE) quantifies the maximum expected difference between the sample estimate and the true population value at a given confidence level.

For a sample statistic \(\hat{\theta}\) (e.g., sample mean or proportion), the confidence interval is:

\[\hat{\theta} \pm \text{Margin of Error}\]

And the margin of error is:

\[\text{MoE} = z^* \cdot SE\]

Where:

\(z^*\) is the critical value from the Z-distribution or T-distribution
\(SE\) is the standard error of the estimate

A smaller margin of error indicates higher precision. It’s a function of both the confidence level and sample variability.

Level of Confidence

The confidence level reflects how confident we are that the interval contains the true population parameter.

Typical levels:

90%: more narrow, less conservative
95%: standard in most analyses
99%: wider interval, more conservative

The confidence level determines the critical value used:

Confidence Level	Z* (approx.)
90%	1.645
95%	1.960
99%	2.576

Higher confidence means wider intervals (to cover more potential outcomes), and lower confidence yields narrower intervals.

Width of the Interval and Trade-offs

The width of a confidence interval reflects the precision of our estimate:

\[\text{Width} = 2 \cdot z^* \cdot SE\]

Key trade-offs:

Higher confidence → wider interval
Larger sample size → smaller standard error → narrower interval
Greater variability in data → larger standard error → wider interval

In practice, you balance the need for precision (narrower intervals) with confidence (coverage).

Impact of Sample Size on CI Width

One of the most influential factors affecting confidence intervals is sample size. Larger samples provide more information, reduce variability, and thus lead to tighter intervals.

Mathematically:

\[SE = \frac{\sigma}{\sqrt{n}} \quad \Rightarrow \quad \text{MoE} \propto \frac{1}{\sqrt{n}}\]

Doubling the sample size does not halve the margin of error—it reduces it by a factor of \(\sqrt{2}\). To halve the margin of error, you must quadruple the sample size.

This principle is especially important in:

Planning experiments
Designing surveys
Estimating budget needs for large-scale studies

Applications of Confidence Intervals

Understanding and applying confidence intervals is fundamental in many areas of data science:

1. Reporting Model Interpretability and Certainty

Rather than reporting a coefficient or score as a fixed number, attaching a CI provides a range that expresses uncertainty. This improves:

Transparency
Interpretability
Communication with domain experts

Example:

Logistic regression coefficient for “income”: 0.45 [95% CI: 0.38, 0.51]

This tells us that even accounting for variability, the income feature has a positive and stable association with the outcome.

2. Designing Reliable A/B/n Experiments

CIs help assess:

Whether observed differences are statistically significant
Whether the effect size is practically meaningful

Example:

Treatment A conversion = 10.2% [CI: 9.7%, 10.8%]
Treatment B conversion = 9.8% [CI: 9.3%, 10.3%]

Since the intervals overlap, the lift might not be significant.

3. Decision-Making Under Uncertainty

In risk modeling or forecasting (e.g., credit risk, fraud, demand prediction), CI bands help quantify potential error:

Predicting revenue next quarter:

Forecast = ₹12.6M [95% CI: ₹11.8M, ₹13.4M]

This range allows decision-makers to plan with a buffer, instead of trusting a single number.

4. Communicating Model Results to Non-technical Stakeholders

CIs help explain variability and uncertainty in a language that makes sense:

“We’re 95% confident that our expected ROI lies between 18% and 22%.”
“Our churn model has an AUC of 0.84 [CI: 0.82, 0.86].”

This builds credibility, avoids overstatement, and supports informed choices.

Hypothesis Testing

Introduction to Hypothesis Testing

Hypothesis testing is a central tool in statistics used to make decisions or inferences about populations based on sample data. It helps us answer questions like:

“Is this new marketing strategy more effective than the old one?” “Do customers from two regions behave differently?” “Does the new version of the model actually perform better than the old one—or is the difference just random?”

Instead of assuming that patterns we see in a dataset are always meaningful, hypothesis testing asks us to challenge our assumptions using probability and sampling theory.

The process works by assuming a null hypothesis (status quo or no difference), collecting data, and then checking whether the evidence is strong enough to reject that assumption in favor of an alternative hypothesis.

What is Hypothesis Testing? Logic and Structure

At its heart, hypothesis testing is a way to make a decision from data. We start by assuming the “status quo” is true (the null hypothesis) and then look at our evidence (the sample data) to decide whether this assumption still seems reasonable.

Here’s a simplified breakdown of the full hypothesis testing procedure:

Step 1: State the Hypotheses

This is the first and most crucial step. We clearly define:

Null Hypothesis (\(H_0\)): There’s no effect or difference. It represents the default or existing belief.
Alternative Hypothesis (\(H_1\) or \(H_a\)): There is an effect or difference. It’s what you hope to find evidence for.

Example: Suppose you launch a new recommendation system and want to check if it leads to more purchases.

\(H_0\): The new system performs the same as the old one (no change)
\(H_1\): The new system increases purchases (positive change)

Step 2: Choose a Significance Level (α)

This is your tolerance for risk—specifically, the risk of a false alarm (rejecting the null when it’s actually true).

Most common choices are 0.05 (5%) or 0.01 (1%)
Choosing α = 0.05 means you’re willing to accept a 5% chance of a false positive

In practice:

Use α = 0.01 in high-stakes situations (e.g., medicine)
Use α = 0.05 for typical business decisions

Step 3: Choose the Appropriate Test and Calculate the Test Statistic

Depending on the type of data and hypothesis, you choose a statistical test:

Comparing means → use t-test or z-test
Comparing proportions → z-test for proportions
Categorical data → chi-square test

You convert your sample result into a test statistic (like a z-score or t-score) that measures how far your observed result is from what we’d expect under the null hypothesis.

Example: You observe a difference of 2% in conversion rate. The z-score might tell you that this difference is 2.1 standard errors away from the expected value under \(H_0\).

Step 4: Compute the p-value or Compare to a Critical Value

Now you determine how likely it would be to observe a result like yours if the null hypothesis were true. This is your p-value.

A small p-value (e.g., < 0.05) means your result is unlikely under the null → reject \(H_0\)
A large p-value suggests your result is likely under the null → do not reject \(H_0\)

Alternatively, you can use a critical value from a distribution (e.g., z = ±1.96 for 95%) and check whether your test statistic falls in the rejection region.

Step 5: Make a Decision

If p-value < α, you reject the null hypothesis. The evidence supports the alternative.
If p-value ≥ α, you do not reject the null. There’s not enough evidence to support the alternative.

Note: You never “accept” the null—you just fail to reject it when the evidence is weak.

Example Recap: You’re testing whether your new ad campaign leads to higher conversions. If your test gives a p-value of 0.03 and you chose α = 0.05, you reject the null and conclude that the new campaign likely improved conversions.

This decision-making framework underlies everything from A/B testing and drug trials to evaluating model improvements.

If p-value < α → reject the null hypothesis
Otherwise, fail to reject the null

Example: You test a new ad campaign. 10% of users in the old campaign converted. Your new campaign shows 12%. Is this difference real?

Set up hypotheses:

\(H_0\): New and old campaigns have the same conversion rate
\(H_1\): New campaign is better (higher conversion)

Run the test, calculate p-value. If it’s below α = 0.05, you conclude the improvement is statistically significant.

Null and Alternative Hypotheses

Null Hypothesis (H₀): The default assumption; no effect, no difference
Alternative Hypothesis (H₁ or Hₐ): What we want to test for; there is an effect or difference

Example: Testing a new drug

\(H_0\): The new drug is no more effective than the current one (mean difference = 0)
\(H_1\): The new drug is more effective (mean difference > 0)

Mathematically: \(H_0: \mu = \mu_0 \quad \text{vs.} \quad H_1: \mu \ne \mu_0\)

One-tailed vs. Two-tailed Tests

Two-tailed: Checks for any difference (≠)
One-tailed: Checks for directional effect (greater than or less than)

Choosing the direction matters:

Use two-tailed when unsure of direction or want to detect any change
Use one-tailed when you’re only interested in improvement or decline

Key Concepts

p-Value

The p-value is one of the most commonly used—but often misunderstood—concepts in hypothesis testing.

To understand it better, imagine this: You believe that a coin is fair, but you flip it 10 times and it lands heads 9 times. You start to wonder—was this just luck, or is the coin biased?

This is the kind of question p-values help us answer.

The p-value is the probability of getting results as extreme as (or more extreme than) what you observed, if the null hypothesis were true.

It does not tell you the probability that the null hypothesis itself is true. Instead, it quantifies how surprising your data would be under the assumption that the null is true.

Let’s break this down more clearly:

A low p-value (typically below 0.05) means the observed result is unlikely under the null hypothesis. This suggests that what you saw is probably not just due to chance, and you may choose to reject \(H_0\).
A high p-value means the data are quite compatible with the null hypothesis—there’s no strong reason to reject it.

Real-world example:

You run an A/B test to compare two landing pages. Version A is the control, Version B is new. Out of 1000 visitors, A converts 100 (10%), and B converts 120 (12%).

Now you ask: Is this 2% difference due to the new design, or just random chance?

You perform a statistical test and get a p-value = 0.03. This means:

“If there were no true difference between A and B, there’s only a 3% chance that I would observe a difference as big as 2%, or bigger, just by random sampling.”

Because 0.03 < 0.05, you reject \(H_0\) and say the new version likely performs better.

But remember: A p-value doesn’t measure the size of the effect, nor does it confirm the alternative hypothesis. It just tells you whether your data are surprising under the null assumption.

Also:

A small p-value ≠ strong effect
A large p-value ≠ no effect

Always consider the p-value alongside effect size and context.

We’ll return to these trade-offs when we discuss errors, power, and confidence intervals in the next sections.

Significance Level (α) and Confidence Level

The significance level (α) is a threshold you choose before running a test.
- Common values: 0.05, 0.01
- If your p-value is less than α, you reject the null
The confidence level is related to α: \(\text{Confidence Level} = 1 - \alpha\)
- α = 0.05 → 95% confidence level

Analogy:

If you test at α = 0.05, you’re allowing a 5% chance of making a Type I error — falsely rejecting a true null hypothesis.

Why not always use a tiny α (like 0.0001)?

Because making α too small increases the risk of Type II errors (missing real effects)
There’s always a tradeoff between caution and power

Example: In medical trials, α = 0.01 is often used to reduce the chance of falsely approving an ineffective drug. But in A/B testing for a website layout, α = 0.05 might suffice.

Type I and Type II Errors

Decision \ Reality	H₀ True	H₁ True
Reject H₀	Type I Error (α)	Correct Decision
Fail to Reject H₀	Correct Decision	Type II Error (β)

Type I Error (α): False positive — rejecting a true null
Type II Error (β): False negative — failing to detect a real effect

Power of a Test

The power of a test is:

\[\text{Power} = 1 - \beta\]

It is the probability of correctly rejecting the null when the alternative is true.

Higher power reduces the chance of a false negative and is affected by:

Sample size (larger = more power)
Effect size (larger = easier to detect)
Significance level (higher α = more power but more risk of Type I)

Effect Size

Effect size quantifies the magnitude of the difference or effect, independent of sample size.

Common measures:

Cohen’s d (difference in means): \(d = \frac{\mu_1 - \mu_2}{s}\)
Pearson’s r (correlation strength)
Odds Ratio or Relative Risk (for proportions)

Why it matters:

A statistically significant result may have a small effect
A large effect may be missed if sample size is small

Confidence Intervals in Hypothesis Testing

CIs can be used as an alternative to hypothesis testing:

If a CI excludes the null value (e.g., zero difference), reject \(H_0\)
If a CI includes the null value, there isn’t enough evidence to reject \(H_0\)

Example: If 95% CI for mean difference = [1.2, 3.5], we’re confident the effect is positive.

CI-based reasoning is more intuitive than binary p-value cutoffs and better for communication.

Sample Size Considerations

Sample size affects:

Power of the test
Margin of error
Precision of parameter estimates

Mathematically:

\[SE = \frac{\sigma}{\sqrt{n}} \quad \Rightarrow \quad \text{Power} \propto \sqrt{n}\]

Increasing sample size:

Reduces standard error
Narrows confidence intervals
Increases chance of detecting true effects (higher power)

But also:

Increases cost and complexity
Can make trivial effects statistically significant

Visual Example: Power Curves

import statsmodels.stats.power as smp
import matplotlib.pyplot as plt

# Power vs Sample Size
effect_size = 0.5  # medium effect
alpha = 0.05
power = 0.8
sample_sizes = range(5, 200)
powers = [smp.TTestIndPower().power(effect_size=effect_size, nobs1=n, alpha=alpha, ratio=1.0) for n in sample_sizes]

plt.figure(figsize=(10, 5))
plt.plot(sample_sizes, powers, label='Power Curve', color='blue')
plt.axhline(y=0.8, color='red', linestyle='--', label='Target Power (0.8)')
plt.title('Effect of Sample Size on Statistical Power')
plt.xlabel('Sample Size per Group')
plt.ylabel('Power')
plt.legend()
plt.grid(True)
plt.show()

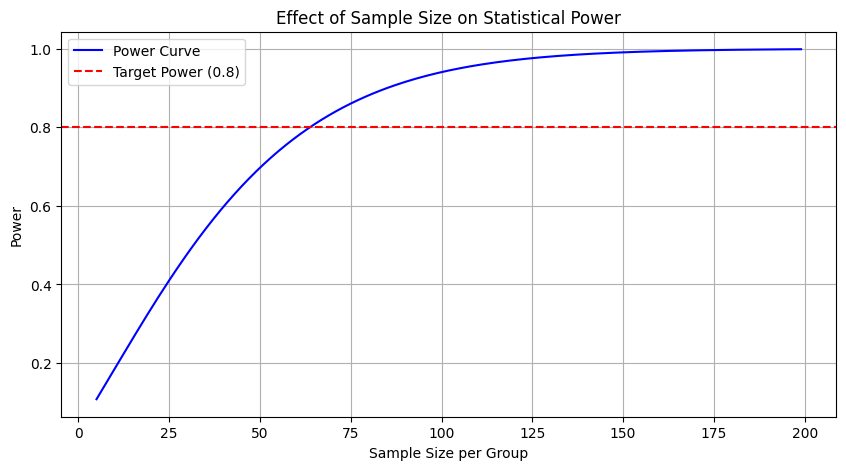
Figure: Effect of Sample Size on Statistical Power

Foundations of hypothesis testing blend logical structure, statistical rigor, and thoughtful design decisions. Every test we run in data science — whether in product experiments, model validation, or causal inference — builds on this groundwork. Mastering these ideas is key to conducting robust, interpretable, and honest data analysis.

Parametric Tests (For Continuous/Numerical Data)

Parametric tests are statistical tests that rely on certain assumptions about the data—most notably, that the data follow a normal distribution and that key parameters such as the population variance are either known or can be reliably estimated. These tests are powerful when their assumptions are satisfied.

In this section, we explore three families of parametric tests commonly used in data science:

Z-tests (when population variance is known)
T-tests (when population variance is unknown)
ANOVA (Analysis of Variance) (for comparing more than two groups)

Z-Test

Z-tests are appropriate when:

The sample size is large (typically \(n \geq 30\))
The population variance \(\sigma^2\) is known
The data is approximately normally distributed

One-sample Z-test

Used when comparing the mean of a sample to a known population mean.

Hypotheses: \(H_0: \mu = \mu_0 \quad vs \quad H_1: \mu \ne \mu_0\)

Test statistic: \(Z = \frac{\bar{x} - \mu_0}{\sigma / \sqrt{n}}\)

Where:

\(\bar{x}\) = sample mean
\(\mu_0\) = hypothesized population mean
\(\sigma\) = known population standard deviation
\(n\) = sample size

Example: Suppose a machine fills soda bottles with an average of 500ml. A random sample of 40 bottles has a mean of 495ml. The population standard deviation is 10ml. Is the machine underfilling?

\[Z = \frac{495 - 500}{10 / \sqrt{40}} \approx -3.16\]

Compare this to the critical value for α = 0.05 (two-tailed): ±1.96. Since −3.16 < −1.96, we reject \(H_0\).

Two-sample Z-test

Used to compare the means of two independent populations, assuming known and equal population variances.

Test statistic: \(Z = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2}}}\)

Where \(\bar{x}_1, \bar{x}_2\) are the sample means, and \(\sigma_1^2, \sigma_2^2\) are the known population variances.

T-Test

T-tests are used when the population variance is unknown and must be estimated from the sample.

One-sample T-test

Used to test whether a sample mean differs from a known value.

Test statistic: \(T = \frac{\bar{x} - \mu_0}{s / \sqrt{n}} \quad \text{with } n-1 \text{ degrees of freedom}\)

Where \(s\) is the sample standard deviation.

Independent Two-sample T-test

Used to compare the means of two independent groups.

Test statistic (equal variance): \(T = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{s_p^2(\frac{1}{n_1} + \frac{1}{n_2})}}\)

Where \(s_p^2\) is the pooled variance: \(s_p^2 = \frac{(n_1 - 1)s_1^2 + (n_2 - 1)s_2^2}{n_1 + n_2 - 2}\)

If variances are unequal, use Welch’s t-test.

Paired T-test

Used when comparing before-and-after values for the same subjects (e.g., A/B testing where users see both versions).

Test statistic: \(T = \frac{\bar{d}}{s_d / \sqrt{n}} \quad \text{with } n - 1 \text{ degrees of freedom}\)

Where:

\(\bar{d}\) = mean of differences
\(s_d\) = standard deviation of differences

Use-cases in Data Science:

Comparing model performance (e.g., RMSE of Model A vs Model B on same test sets)
Evaluating A/B tests where users interact with both treatments

ANOVA (Analysis of Variance)

Used to compare more than two groups. While t-tests compare two means, ANOVA tests whether at least one group mean is different from the others.

One-way ANOVA

Tests whether \(k\) groups have equal means.

Hypotheses:

\(H_0\): All group means are equal
\(H_1\): At least one group mean is different

Test statistic: \(F = \frac{\text{Between-group variance}}{\text{Within-group variance}} = \frac{MS_B}{MS_W}\)

Where:

\(MS_B = \frac{\text{SSB}}{k - 1}\) (Mean Square Between)
\(MS_W = \frac{\text{SSW}}{N - k}\) (Mean Square Within)

The higher the F-statistic, the more likely it is that at least one group mean differs significantly.

Assumptions:

Groups are independent
Residuals are normally distributed
Equal variance across groups (homogeneity of variances)

Post-hoc Testing

ANOVA tells us if at least one group is different, but it doesn’t say which groups differ. That’s where post-hoc tests come in.

One of the most widely used post-hoc tests is Tukey’s HSD (Honestly Significant Difference). It controls the family-wise error rate, meaning the chance of making at least one Type I error across all comparisons.

Tukey’s HSD Test Formula:

For any pair of group means \(\bar{x}_i, \bar{x}_j\): \(\text{HSD}_{i,j} = |\bar{x}_i - \bar{x}_j|\)

This difference is then compared against a critical value: \(q_{\alpha} \cdot \sqrt{\frac{MS_W}{n}}\)

Where:

\(q_{\alpha}\) is the Studentized range statistic (depends on \(\alpha\), number of groups, and degrees of freedom)
\(MS_W\) is the within-group mean square from ANOVA
\(n\) is the number of observations per group (if equal)

If the observed \(\text{HSD}_{i,j}\) is greater than the critical value, the difference between groups \(i\) and \(j\) is considered statistically significant.

When to Use:

Only after obtaining a significant F-statistic from ANOVA
Use when you’re comparing all possible pairs of group means

Extensions

Two-way ANOVA

Use case: You want to analyze how two independent categorical variables affect a single continuous response variable.

Example:

Factor A: Region (North, South, East, West)
Factor B: Gender (Male, Female)
Response: Monthly Spend

Model: \(Y_{ijk} = \mu + \alpha_i + \beta_j + (\alpha\beta)_{ij} + \epsilon_{ijk}\)

Where:

\(\alpha_i\) is the effect of the i-th level of factor A
\(\beta_j\) is the effect of the j-th level of factor B
\((\alpha\beta)_{ij}\) is the interaction effect between the two factors
\(\epsilon_{ijk}\) is the error term

You get F-statistics for:

Main effect of A
Main effect of B
Interaction effect of A × B

Why it matters:
You can test not just individual factor effects but also whether their combination influences the outcome differently than you’d expect by summing their separate effects.

Repeated Measures ANOVA

Use case: The same subjects are measured multiple times under different conditions or time points.

Example:

You track customer satisfaction before, during, and after a product change
Each user gives ratings at three points: \(T_1, T_2, T_3\)

The model accounts for correlation between repeated measurements within the same subject.

Model outline: \(Y_{ij} = \mu + \tau_j + s_i + \epsilon_{ij}\)

Where:

\(\tau_j\) is the treatment/time effect
\(s_i\) is the subject-specific random effect
\(\epsilon_{ij}\) is residual error

Key difference from regular ANOVA:

Repeated Measures ANOVA accounts for the fact that responses from the same subject are not independent
Reduces variability due to subject-level differences

Common Applications:

Longitudinal studies
A/B/C tests with time-based measurements
Evaluating model performance over time on evolving datasets

… (existing content above remains unchanged) …

Non-Parametric Alternatives (When Assumptions Don’t Hold)

Parametric tests rely on strong assumptions—like normality of data, known variance, and equal group variances. But in the real world, these assumptions often fail:

Data might be skewed
Variances may differ
Sample sizes may be small

Non-parametric tests provide robust alternatives when such assumptions don’t hold. They don’t estimate parameters like mean and standard deviation directly—instead, they use rank-based or simulation-based logic.

We’ll explore four key non-parametric methods:

Mann–Whitney U Test (Wilcoxon Rank-Sum Test)

Used to compare two independent groups when data is not normally distributed.

Hypotheses:

\(H_0\): The distributions of both groups are equal
\(H_1\): One group tends to have higher values than the other

Procedure:

Combine both groups
Rank all observations
Calculate the U statistic:

Let \(R_1\) be the sum of ranks in group 1 (size \(n_1\)), and \(R_2\) for group 2 (size \(n_2\)):

\[U_1 = R_1 - \frac{n_1(n_1 + 1)}{2} \quad\] \[\quad U_2 = R_2 - \frac{n_2(n_2 + 1)}{2}\]

The final U-statistic is: \(U = \min(U_1, U_2)\)

When to use:

Comparing conversion rates from two regions
Comparing response times between two systems when distributions are skewed

Wilcoxon Signed-Rank Test

Used for paired samples or matched data when normality is violated (non-parametric version of the paired t-test).

Hypotheses:

\(H_0\): The median of differences is zero
\(H_1\): The median of differences is not zero

Procedure:

Compute differences between paired values
Remove zero differences
Rank absolute differences
Add ranks for positive and negative signs separately

Test statistic is the smaller of the two rank sums.

When to use:

Comparing user engagement before vs. after feature launch when the metric is not normally distributed
Evaluating model accuracy improvements per user

Kruskal–Wallis Test

Used to compare more than two independent groups, where ANOVA assumptions don’t hold.

Hypotheses:

\(H_0\): All group distributions are equal
\(H_1\): At least one group distribution differs

Procedure:

Combine all data and assign ranks
Calculate test statistic:

Let:

\(R_i\) = sum of ranks for group \(i\)
\(n_i\) = size of group \(i\)
\(N\) = total sample size

Then: \(H = \left( \frac{12}{N(N+1)} \right) \sum_{i=1}^k \frac{R_i^2}{n_i} - 3(N+1)\)

Under \(H_0\), H approximately follows a \(\chi^2\) distribution with \(k-1\) degrees of freedom.

When to use:

Comparing multiple ML models on non-normal evaluation metrics
Comparing satisfaction ratings across multiple locations with skewed responses

Permutation Testing (Randomization Test)

A powerful and flexible simulation-based method. You compute the test statistic (e.g., mean difference) on your data and then simulate the null distribution by shuffling labels or outcomes many times.

Steps:

Calculate original test statistic (e.g., \(\bar{x}_1 - \bar{x}_2\))
Randomly shuffle group labels and compute new test statistic
Repeat thousands of times to generate null distribution
Compute p-value as proportion of permuted statistics more extreme than observed

Why it works: If the null hypothesis is true, labels (e.g., treatment/control) should be interchangeable

When to use:

Testing significance in ML model improvements
A/B testing with small or unusual datasets
Any metric without known parametric distribution

Non-parametric methods are crucial when data breaks assumptions. They offer robustness at the cost of some power, but in return provide trustable results where parametric tests might mislead.

Next, we’ll explore how these tests connect with categorical data analysis using Chi-square tests and tests for proportions.

Categorical Data: Chi-Square and Proportions

When dealing with categorical variables (e.g., gender, yes/no responses, user type), we can’t use tests for means or variances. Instead, we rely on count-based tests to evaluate hypotheses. The two major tools here are the Chi-square family of tests and Z-tests for proportions.

Chi-Square Tests

Chi-square (\(\chi^2\)) tests compare observed counts with expected counts. They’re used to assess whether:

A categorical variable follows a specified distribution
Two categorical variables are independent

A. Goodness-of-Fit Test

Used to test whether a single categorical variable matches an expected distribution.

Example: You survey users about preferred platform (Web, Android, iOS). You expect equal preference (1/3 each), but the observed counts differ. Is this difference due to chance?

Hypotheses:

\(H_0\): The observed distribution matches the expected
\(H_1\): The observed distribution is different

Test statistic: \(\chi^2 = \sum_{i=1}^{k} \frac{(O_i - E_i)^2}{E_i}\) Where:

\(O_i\) = Observed count for category \(i\)
\(E_i\) = Expected count for category \(i\)

Degrees of freedom: \(df = k - 1\)

If \(\chi^2\) is large (with a small p-value), we reject \(H_0\).

B. Test of Independence (Contingency Table)

Used to determine if two categorical variables are independent.

Example: Are platform (Web, iOS, Android) and subscription status (Paid, Free) independent?

Data is arranged in a contingency table. Expected counts are computed assuming independence: \(E_{ij} = \frac{(\text{Row Total})_i \cdot (\text{Column Total})_j}{\text{Grand Total}}\)

Chi-square test statistic: \(\chi^2 = \sum_{i=1}^{r} \sum_{j=1}^{c} \frac{(O_{ij} - E_{ij})^2}{E_{ij}}\) Where:

\(r\) = number of rows, \(c\) = number of columns
\[df = (r - 1)(c - 1)\]

When to use:

Analyzing click-through rate vs ad category
Purchase rate by device type

Z-tests for Proportions

Z-tests for proportions compare the percentage or rate of a binary outcome across one or two samples.

A. One-Proportion Z-test

Used to compare an observed proportion to a known/hypothesized population proportion.

Example: You expect 20% of users to click a button. You observe 70 clicks out of 300. Is this deviation significant?

Hypotheses:

\[H_0: p = p_0\]
\[H_1: p \ne p_0\]

Test statistic: \(Z = \frac{\hat{p} - p_0}{\sqrt{\frac{p_0(1 - p_0)}{n}}}\) Where:

\(\hat{p} = \frac{x}{n}\) is the sample proportion

B. Two-Proportion Z-test

Used to compare two sample proportions.

Example: In an A/B test:

Version A: 35/200 clicks
Version B: 50/220 clicks

Hypotheses:

\[H_0: p_1 = p_2\]
\[H_1: p_1 \ne p_2\]

Pooled proportion: \(\hat{p} = \frac{x_1 + x_2}{n_1 + n_2}\)

Test statistic: \(Z = \frac{\hat{p}_1 - \hat{p}_2}{\sqrt{\hat{p}(1 - \hat{p})\left(\frac{1}{n_1} + \frac{1}{n_2}\right)} }\)

Interpretation: A large absolute Z and small p-value suggests a real difference between the proportions.

Applications

A/B Testing: Click-through or conversion rate comparisons using 2-proportion Z-tests
Survey Analysis: Checking preference or brand distribution via goodness-of-fit
Behavioral Segmentation: Whether usage frequency differs by user type via test of independence

These tests are essential when your outcome is categorical (clicked or not, paid or free, yes or no) and need to be modeled or evaluated accordingly.

Some Additional Theories

This section delves into the mathematical bedrock of hypothesis testing, including how optimal tests are constructed and how modern perspectives such as Bayesian reasoning compare to classical frameworks. These ideas underpin many test procedures used across science and data analytics.

Neyman–Pearson Lemma

The Neyman–Pearson Lemma provides a rigorous way to design the most powerful test for a given size (i.e., Type I error rate) when testing simple hypotheses.

Problem Setup

You are testing: \(H_0: \theta = \theta_0 \quad \text{vs.} \quad H_1: \theta = \theta_1\) where both \(\theta_0\) and \(\theta_1\) are simple, fully specified values.

The Lemma

Let \(L(\theta; x)\) be the likelihood of data \(x\) under parameter \(\theta\). Then the most powerful test at significance level \(\alpha\) rejects \(H_0\) if: \(\Lambda(x) = \frac{L(\theta_0; x)}{L(\theta_1; x)} \leq k\) for some constant \(k\) chosen to ensure the desired Type I error rate.

Intuition

This says: compare the likelihoods under the null and alternative. If the data is far more likely under \(H_1\) than under \(H_0\), you should reject \(H_0\).

Example

Suppose you are testing whether a coin is fair (\(\theta_0 = 0.5\)) or biased towards heads (\(\theta_1 = 0.7\)). You flip the coin 10 times and observe 8 heads.

Under \(H_0\): \(P(X = 8) = {10 \choose 8}(0.5)^8(0.5)^2 = 0.044\)
Under \(H_1\): \(P(X = 8) = {10 \choose 8}(0.7)^8(0.3)^2 = 0.233\)

Then: \(\Lambda(x) = \frac{0.044}{0.233} \approx 0.189\)

If this falls below the critical threshold \(k\) determined by \(\alpha\), we reject \(H_0\).

Likelihood Ratio Tests (LRT)

Likelihood Ratio Tests generalize the Neyman–Pearson idea to composite hypotheses: \(H_0: \theta \in \Theta_0 \quad \text{vs.} \quad H_1: \theta \in \Theta_1\)

Test Statistic

Define the likelihood ratio: \(\lambda(x) = \frac{\sup_{\theta \in \Theta_0} L(\theta; x)}{\sup_{\theta \in \Theta} L(\theta; x)}\)

Often we use the log-likelihood ratio: \(-2 \log \lambda(x)\)

Under regularity conditions, this follows a chi-square distribution with degrees of freedom equal to the difference in parameters between the full and reduced models.

Example: Logistic Regression Variable Selection

Let’s say you’re modeling whether a user subscribes (yes/no) based on their activity.

\(M_0\): Model with one feature (page_views)
\(M_1\): Model with two features (page_views and time_spent)

You compute: \(\log L_0 = -120.5 \quad , \quad \log L_1 = -110.3\)

Then the test statistic is: \(-2(\log L_0 - \log L_1)\)

\[= -2(-120.5 + 110.3) = 20.4\]

Compare this to a \(\chi^2\) distribution with 1 df. If the p-value is below 0.05, conclude that time_spent significantly improves the model.

Bayesian Perspective (Brief Mention)

The Bayesian framework treats parameters as random variables and updates belief about them using observed data.

Bayes’ Theorem: \(P(\theta \mid x) = \frac{P(x \mid \theta) P(\theta)}{P(x)}\)

Example: Click-Through Rate (CTR)

Suppose your prior belief is that a new campaign’s CTR is around 5%, and you observe 12 clicks in 100 views.

Prior: \(\theta \sim \text{Beta}(2, 38)\) (mean = 0.05)
Likelihood: Binomial(100, \(\theta\))

Posterior is: \(\theta \mid x \sim \text{Beta}(2 + 12, 38 + 88)\)

\[= \text{Beta}(14, 126)\]

You can now compute:

Posterior mean, mode, variance
Probability that CTR > 6%, etc.

Bayes Factor Example

Suppose:

\(H_0\): CTR = 0.05
\(H_1\): CTR > 0.05 (uniform prior on [0.05, 1])

Compute likelihood under each:

\[P(x \mid H_0) = {100 \choose 12}(0.05)^{12}(0.95)^{88}\]
\[P(x \mid H_1)\]

\[= \int_{0.05}^1 {100 \choose 12} \theta^{12} (1 - \theta)^{88} \cdot \frac{1}{0.95} d\theta\]

Then: \(BF_{10} = \frac{P(x \mid H_1)}{P(x \mid H_0)}\)

If \(BF_{10} > 10\), it provides strong evidence against \(H_0\).

Practical Applications in Data Science

Statistical hypothesis testing is not just a theoretical construct—it plays a critical role in how we evaluate experiments, deploy models, validate features, and uncover patterns in real-world datasets. This section explores how the theoretical ideas discussed earlier are applied concretely in common data science workflows.

A/B Testing

A/B testing is the most common real-world use of hypothesis testing in industry. It’s used to test changes to a product, interface, or marketing campaign.

Hypothesis Testing for Product Experiments

You split your users randomly into two groups:

Group A (Control): Uses the current version
Group B (Treatment): Sees the new variant

You define:

\(H_0\): Conversion rates are equal (no effect)
\(H_1\): Conversion rates are different

Then apply a two-proportion Z-test: \(Z = \frac{\hat{p}_A - \hat{p}_B}{\sqrt{\hat{p}(1 - \hat{p})\left(\frac{1}{n_A} + \frac{1}{n_B}\right)}}\) Where:

\(\hat{p}_A, \hat{p}_B\) = sample proportions for control and treatment
\(\hat{p}\) = pooled proportion

Uplift Measurement, Variant Comparison

Beyond overall significance, you measure uplift: \(\text{Uplift} = \hat{p}_B - \hat{p}_A\) And calculate confidence intervals to see if the lift is practically significant: \(CI = (\hat{p}_B - \hat{p}_A) \pm Z_{1 - \alpha/2} \cdot SE\)

Example: If the new design improves click-through rate from 8% to 10% with a p-value of 0.01 and a 95% CI of (1%, 3%), the test supports both statistical and practical significance.

Validating Model Changes

Statistical Comparison of Model Performance

When introducing a new ML model, you must ensure it’s genuinely better than the existing model—not just on one lucky sample.

Let’s say you compare accuracy or AUC of old vs. new models across multiple test batches or user segments.

You can:

Use a paired t-test if same datasets are used for both models
Use a Wilcoxon signed-rank test if the metric distributions are skewed

Example: You calculate RMSE for both models on 30 test sets:

\(H_0\): Mean difference in RMSE is 0
\(H_1\): New model performs better (lower RMSE)

A significant p-value (e.g., p = 0.002) supports replacing the older model.

Feature Impact Testing

This involves testing whether the distribution of a feature differs across target groups (e.g., churned vs. non-churned users).

Hypothesis Testing to Compare Means or Medians

Use:

Two-sample t-test (for normally distributed features)
Mann–Whitney U test (if non-normal)

Example: Is average time_spent different for users who churned vs. retained?

\(H_0\): Mean time_spent is equal across groups
\(H_1\): Means are different

Significant difference may inform feature selection or model interpretation.

You can also use:

Chi-square test for categorical features (e.g., device type)
ANOVA if there are more than two groups

Bias Detection

Hypothesis testing is critical for detecting unintended bias in models or datasets.

Are Certain User Segments Treated Differently?

Example: Are female users receiving lower credit limits than male users, after adjusting for income?

Split data by segment (e.g., gender)
Compare outcome distribution:
- Use t-test or Mann–Whitney U for numerical outcomes
- Use Chi-square for approval rate differences

Statistical significance here points to disparate impact, which is a signal for deeper investigation or corrective modeling.

Conversion Funnel Analysis

Funnels track sequential steps in a user journey—like:

Homepage View → 2. Product Page → 3. Cart → 4. Checkout

You can apply hypothesis testing to identify where users are dropping off more than expected.

Step-by-Step Significance Testing

For each funnel step:

Compare conversion rates across A/B variants or over time
Use proportion Z-tests or Chi-square tests at each stage

Example:

Cart-to-checkout conversion is 55% in variant A and 60% in variant B
Apply Z-test: \(Z = \frac{0.60 - 0.55}{\sqrt{\hat{p}(1 - \hat{p})(1/n_1 + 1/n_2)}}\) If significant, you’ve found the step that improves overall funnel performance.

Summary & Decision Framework

At this point, we’ve explored the full landscape of hypothesis testing—from the theoretical foundations to real-world data science applications. This section ties everything together and offers a decision-making framework that can guide your use of statistical inference in practice.

When to Use Which Test?

Choosing the right test depends on several factors: data type, number of groups, pairing, and assumptions about the distribution. Here’s a quick guide:

Use Case	Test Type	Notes
Compare one sample mean to known mean	One-sample Z or T-test	Use Z if population std dev is known
Compare means of two independent groups	Two-sample T-test (or Welch)	Welch’s if unequal variances
Compare paired measurements	Paired T-test or Wilcoxon signed-rank	For before/after, same subject designs
Compare multiple group means	ANOVA / Kruskal–Wallis	Kruskal if non-normal
Two categorical variables	Chi-square test of independence	Use contingency tables
One categorical variable vs expected	Chi-square goodness-of-fit	Useful in survey, polling
Binary proportions	Z-test for proportions	A/B testing
Any metric with small samples or unknown distribution	Permutation tests	Flexible and simulation-based

Checklist: Assumptions, Sample Size, Effect Size, and Power

Before running any test, ask yourself:

Is the data approximately normal?
- If not, consider transformations or non-parametric tests.
Are the groups independent or paired?
- Paired tests adjust for within-subject variation.
Do the variances look equal?
- Use Levene’s or F-test. If unequal, use Welch’s correction.
What is the sample size?
- Small samples (<30) require caution—non-parametric tests or bootstrapping are safer.
What is the effect size you care about?
- Even a significant result with tiny effect size may not be practical.
Have you considered statistical power?
- A test with low power might fail to detect a real effect (Type II error).

Pitfalls to Avoid in Real-World Testing

p-hacking: Running multiple tests and only reporting significant ones inflates false positives.
Ignoring assumptions: Applying t-tests on heavily skewed data without checking.
Neglecting context: A result can be statistically significant but operationally irrelevant.
Overfitting validation data: Using test set repeatedly undermines independence.
Overreliance on p-value: Use effect size and confidence intervals as well.

Communicating Results to Stakeholders

How you explain findings is just as important as the analysis itself. Here are some guidelines:

Use Plain Language:
- “We are 95% confident that the conversion rate improvement is between 1% and 3%.”
- Avoid technical jargon unless the audience is statistically trained.
Report Estimates and Uncertainty:
- Always show the confidence interval and sample sizes.
Focus on Practical Relevance:
- “This feature speeds up customer onboarding by 2 days on average—significant at p < 0.01.”
Visualize Results:
- Use error bars, histograms of distributions, or funnel plots to support your claims.
Clarify Limitations:
- “This test is based on 1 week of data; longer-term patterns may differ.”

As we wrap up this deep dive into statistical inference, it’s worth stepping back to ask: what is all this for?

Beneath every test statistic and p-value lies a deeper intention—not just to prove something, but to learn something. Whether you’re designing experiments, validating models, or evaluating product impact, inference gives you a structured way to reason under uncertainty.

And sometimes, the most powerful insights don’t come from the numbers themselves—but from how you read them.

In 1933, a brilliant young mathematician named Abraham Wald fled rising fascism in Austria and eventually took refuge in the United States. By the early 1940s, he was working with the U.S. military as part of the Statistical Research Group at Columbia University, tasked with one critical question: how could they help protect Allied bombers returning from missions over Europe?

Wald was handed data on aircraft that had returned from battle, annotated with diagrams showing where the planes had sustained bullet damage. Most of the hits clustered on the wings and tail sections. Military officials initially suggested reinforcing those areas.

But Wald paused. He looked at the data and asked a different question—not where are planes hit, but where are planes not returning from being hit?

He realized that the military was only seeing the planes that made it home. Any aircraft that had taken hits in the engine or cockpit likely didn’t return—and therefore weren’t part of the dataset.

His recommendation? Reinforce the parts without bullet holes in the sample—because their absence was evidence of fatal hits.

Wald’s insight didn’t rely on more data, but on understanding the bias in the data they already had. It was a masterclass in inference: seeing not only what is present, but noticing what is missing—and recognizing that absence can be the loudest signal.

This wasn’t just a clever trick. It saved lives. And it stands today as a profound lesson in how careful reasoning, clear framing, and statistical thinking can make all the difference.

That’s what hypothesis testing prepares us for—not just to compute, but to question. To know when the data speaks clearly, when it lies in whispers, and when what’s unsaid may matter most.

In your journey as a data scientist, may you carry Wald’s clarity, humility, and curiosity.