Markov Chains, Hidden Markov Models & Probabilistic Sequence Modeling
- Markov Chains
- Hidden Markov Models (HMMs)
- Forward-Backward Algorithm
- Numerical Example: Forward-Backward on a Toy HMM
- Viterbi Decoding
- Markov Chain Monte Carlo (MCMC)
- Metropolis-Hastings Algorithm
- Gibbs Sampling
- Visualizing the Sampling Process
- Markov Decision Processes (MDPs): Modeling Decision-Making Over Time
- Applications in Practice
- Conclusion: A Markovian Mindset
In the late 19th century, a Russian mathematician named Andrey Markov found himself in a battle—not with another scholar, but with the prevailing belief that randomness was chaos, and that independence was the only tractable form of uncertainty. Markov, ever the contrarian, wanted to prove that dependence—even just on the immediate past—could still be mathematically elegant.
So in 1906, he analyzed poetry. He looked at the sequence of vowels and consonants in Pushkin’s Eugene Onegin, testing whether the likelihood of one letter depended on the previous one. What emerged was a bold idea: you could model a sequence with memory—just not too much memory. And that’s how the Markov Chain was born.
Let’s start with a question: if you know where you are, do you know where you’re going next? In probabilistic modeling, the answer often depends on how much of the past matters.
That’s where Markov chains step in. They are built on a beautiful assumption that the future depends only on the present, not the past. This idea—called the Markov property—forms the spine of a powerful family of models used in everything from natural language processing to biology, finance, and reinforcement learning.
We’ll take a detailed walk through:
- Markov Chains and their mathematical formulation
- The Markov Property, Transition Matrices, and Stationary Distributions
- Hidden Markov Models (HMMs), where you can’t even see the states
- The forward-backward algorithm and its intuition
- Real-world applications in data science
Let’s begin at the start: what does it mean to model a sequence probabilistically?
Markov Chains
To understand Markov Chains, we first need to step back and think about what a stochastic process is. A stochastic process is a sequence of random variables indexed by time. It models systems that evolve over time with inherent randomness. A Markov Chain is a special type of stochastic process with a unique and powerful assumption: the Markov property.
What is a Markov Chain?
A Markov Chain is a discrete-time stochastic process \(\{X_0, X_1, X_2, \dots\}\) that satisfies the condition:
\[P(X_{t+1} = x_{t+1} \mid X_t = x_t, X_{t-1} = x_{t-1}, \dots, X_0 = x_0) = P(X_{t+1} = x_{t+1} \mid X_t = x_t)\]This is the Markov property. It means that the future is conditionally independent of the past, given the present.
A Markov Chain is fully specified by:
- A state space \(S = \{s_1, s_2, \dots, s_n\}\)
- A transition matrix \(P \in \mathbb{R}^{n \times n}\), where each entry \(P_{ij}\) gives the probability of transitioning from state \(i\) to state \(j\):
- An initial distribution \(\pi^{(0)}\), where \(\pi^{(0)}_i = P(X_0 = s_i)\)
Now, imagine a board game where you roll a die and move between rooms. The next room you land in depends only on your current room and the die—not on how you got there. That’s the core idea behind a Markov Chain.
In customer behavior modeling, this idea is often used: a person browsing an online store might move from “Homepage” to “Product Page” to either “Add to Cart” or “Exit”. What they do next depends on where they are now—not what sequence of pages led them there.
Transition Matrix (with Example)
Let’s say we have three states: \(A = \text{Browsing}\), \(B = \text{Cart}\), and \(C = \text{Checkout}\). From real data, we estimate the following transition probabilities:
\[P = \begin{bmatrix} 0.6 & 0.3 & 0.1 \\ 0.2 & 0.5 & 0.3 \\ 0.1 & 0.1 & 0.8 \\ \end{bmatrix}\]Each row corresponds to the current state, and each column to the next state. For example, if a user is in the “Cart” state (row 2), they have a 20% chance of going back to browsing, 50% chance of staying in cart, and 30% chance of going to checkout.
We ensure that:
\[\sum_{j=1}^n P_{ij} = 1 \quad \text{for all } i\]This matrix allows us to compute the probability distribution over states at time \(t+1\) from the distribution at time \(t\):
\[\pi^{(t+1)} = \pi^{(t)} P\]This is a simple matrix-vector product, which makes computation efficient and elegant.
Stationary Distribution (Long-Term Behavior)
A natural question arises: if we let a Markov chain evolve over time, does it settle into a consistent probabilistic behavior, regardless of the initial state? This leads us to the concept of a stationary distribution.
A stationary distribution \(\pi\) is a vector such that:
\[\pi = \pi P\]This means that if the chain starts with the distribution \(\pi\), then the distribution over states remains \(\pi\) at all future time steps. In other words, it is invariant under the transition dynamics of the chain.
More precisely, let \(P \in \mathbb{R}^{n \times n}\) be a transition matrix of a time-homogeneous Markov chain over \(n\) discrete states. We want to find \(\pi \in \mathbb{R}^n\) such that:
\[\pi_i = \sum_{j=1}^{n} \pi_j P_{ji}, \quad \forall i \in \{1, ..., n\}\]and
\[\sum_{i=1}^n \pi_i = 1, \quad \pi_i \geq 0\]This is a left-eigenvector equation: \(\pi\) is a (left) eigenvector of \(P\) with eigenvalue 1, normalized to sum to 1.
Why does a stationary distribution exist?
If a Markov chain is irreducible (it is possible to reach any state from any other) and aperiodic (the chain does not get stuck in deterministic cycles), then there exists a unique stationary distribution, and regardless of where you start, the distribution of states \(X_t\) will converge to \(\pi\) as \(t \to \infty\).
This is known as the Ergodic Theorem for Markov chains.
Application: Long-run behavior modeling
In credit scoring models, banks use Markov chains to model the evolution of credit ratings (AAA, AA, A, BBB, BB, etc.). The stationary distribution tells them the steady-state risk exposure of their portfolio.
In biological sequence modeling, suppose you model DNA base transitions using a Markov chain with states \(\{A, T, G, C\}\). The stationary distribution gives the expected frequency of each base in the long term—important in evolutionary biology and genome simulation.
Numerical Example
Let’s revisit the two-state example but solve it with a more formal method.
Given:
\[P = \begin{bmatrix} 0.9 & 0.1 \\ 0.5 & 0.5 \\ \end{bmatrix}\]We want to solve:
\[\pi = \pi P\]Let \(\pi = [\pi_1, \pi_2]\). Then we write:
\[\begin{cases} \pi_1 = 0.9 \pi_1 + 0.5 \pi_2 \\ \pi_2 = 0.1 \pi_1 + 0.5 \pi_2 \\ \pi_1 + \pi_2 = 1 \end{cases}\]Subtract the first equation from both sides:
\[\pi_1 - 0.9 \pi_1 - 0.5 \pi_2 = 0 \Rightarrow 0.1 \pi_1 = 0.5 \pi_2\]Now substitute into the normalization condition:
\[\pi_1 + \pi_2 = 1 \Rightarrow \pi_1 + \frac{0.1}{0.5} \pi_1 = 1\]Simplify:
\[\pi_1 (1 + 0.2) = 1 \Rightarrow \pi_1 = \frac{1}{1.2} = \frac{5}{6}, \quad \pi_2 = \frac{1}{6}\]So the long-run distribution is:
\[\pi = \left[\frac{5}{6}, \frac{1}{6}\right]\]Even if we start the process at state 2, over many iterations the proportion of time spent in state 1 will tend to \(83.3\%\).
This property is crucial in Monte Carlo methods, as we’ll later see in MCMC and Gibbs sampling—where convergence to the stationary distribution is the foundation of approximate inference in probabilistic models.
Hidden Markov Models (HMMs)
So far, we’ve assumed that we can observe the state of the system directly. But in many real-world scenarios, this isn’t the case. Often, the system has hidden internal states that we can’t directly see. What we can observe, however, are outputs or emissions that depend probabilistically on those hidden states.
This motivates the Hidden Markov Model—an extension of the Markov Chain where the states are hidden and each state emits observable outputs.
Formal Definition
A Hidden Markov Model is defined by:
- A finite set of hidden states: \(Z = \{z_1, z_2, \dots, z_K\}\)
- A finite set of observations: \(X = \{x_1, x_2, \dots, x_T\}\)
- A transition matrix between hidden states: \(A \in \mathbb{R}^{K \times K}\), where: \(A_{ij} = P(z_{t+1} = j \mid z_t = i)\)
- An emission matrix (or output probability): \(B \in \mathbb{R}^{K \times M}\), where: \(B_{jk} = P(x_t = k \mid z_t = j)\)
- An initial state distribution: \(\pi_i = P(z_1 = i)\)
The generative story of an HMM is:
- Choose initial hidden state \(z_1 \sim \pi\)
- For each time step \(t = 1 \text{ to } T\):
- Generate an observation \(x_t \sim P(x_t \mid z_t)\)
- Transition to the next hidden state \(z_{t+1} \sim P(z_{t+1} \mid z_t)\)
So while the true states \(z_t\) are hidden from us, we observe the emitted sequence \(x_1, \dots, x_T\) and want to reason about the hidden structure.
Example: Part-of-Speech Tagging
In Natural Language Processing (NLP), a common application of HMMs is part-of-speech tagging. Here:
- The words in a sentence are the observed variables
- The grammatical roles (noun, verb, adjective, etc.) are the hidden states
The model learns the likelihood of a word given a part of speech (emission probability) and the likelihood of tag sequences (transition probability). Using the forward-backward algorithm, we can compute how probable each tag is for each word in context.
Forward-Backward Algorithm
When given an HMM and an observation sequence \(x_1, x_2, \dots, x_T\), a key question is:
What is the probability of this sequence under the model?
This is the likelihood of the data:
\[P(x_1, \dots, x_T) = \sum_{z_1, \dots, z_T} P(x_1, \dots, x_T, z_1, \dots, z_T)\]Since the number of possible hidden state sequences grows exponentially with \(T\), brute-force summation is intractable.
The forward-backward algorithm solves this using dynamic programming.
Forward Probabilities
Define:
\[\alpha_t(j) = P(x_1, x_2, \dots, x_t, z_t = j)\]That is, the joint probability of observing the first \(t\) observations and ending in hidden state \(j\).
The recursion proceeds as follows:
-
Initialization:
\[\alpha_1(j) = \pi_j \cdot B_{j}(x_1)\] -
Induction:
\[\alpha_{t}(j) = B_j(x_t) \cdot \sum_i \alpha_{t-1}(i) A_{ij}\] -
Termination:
\[P(x_1, \dots, x_T) = \sum_j \alpha_T(j)\]
Backward Probabilities
Similarly, define:
\[\beta_t(i) = P(x_{t+1}, x_{t+2}, \dots, x_T \mid z_t = i)\]That is, the probability of observing the future sequence starting from time \(t+1\) given hidden state \(i\) at time \(t\).
-
Initialization:
\[\beta_T(i) = 1\] -
Induction:
\[\beta_t(i) = \sum_j A_{ij} B_j(x_{t+1}) \beta_{t+1}(j)\]
Posterior Probabilities
We can now compute the probability of being in state \(j\) at time \(t\) given the entire observed sequence:
\[P(z_t = j \mid x_{1:T}) = \frac{\alpha_t(j) \cdot \beta_t(j)}{P(x_{1:T})}\]This is crucial for tasks such as smoothing (estimating the state at a previous time) or learning model parameters via the EM algorithm.
Before we dive into numbers, let’s unpack what this algorithm is really doing—and why we need it.
In Hidden Markov Models, the actual sequence of states is hidden. But we often want to answer questions like:
- What is the likelihood of the observed data sequence?
- What is the probability that the system was in a particular state at a particular time?
To answer this efficiently, we use the forward-backward algorithm. It does two things:
- Forward pass: Computes the probability of observing the first ( t ) observations and ending in each state.
- Backward pass: Computes the probability of observing the rest of the sequence from each state.
Together, they allow us to calculate the posterior probability of being in any state at any time, given the entire observation sequence. This is crucial for inference, smoothing, and parameter learning (via EM).
Now let’s see it in action.
Numerical Example: Forward-Backward on a Toy HMM
We use a classic example often seen in HMM tutorials: determining whether the weather was Rainy or Sunny based on someone’s activity — Walk, Shop, or Clean.
Model Setup
Hidden states:
- \[Z = \{\text{Rainy}, \text{Sunny}\}\]
Observations:
- \[X = \{\text{Walk}, \text{Shop}, \text{Clean}\}\]
Initial state distribution:
\(\pi = \begin{bmatrix} 0.6 & 0.4 \end{bmatrix}\)
Transition matrix \(A\): \(\begin{bmatrix} 0.7 & 0.3 \\\\ 0.4 & 0.6 \end{bmatrix}\)
Emission matrix \(B\):
(rows: Rainy, Sunny; columns: Walk, Shop, Clean)
Observation sequence:
\(x = [\text{Walk}, \text{Shop}, \text{Clean}]\)
Corresponding to time steps \(t=1,2,3\).
Forward Pass
Let \(\alpha_t(i)\) be the probability of observing the first \(t\) observations and being in state \(i\) at time \(t\).
Step 1: Initialization
From initial distribution and emissions:
\[\alpha_1(\text{Rainy}) = 0.6 \cdot 0.1 = 0.06 \\\\ \alpha_1(\text{Sunny}) = 0.4 \cdot 0.6 = 0.24\]Step 2: Recursion
At \(t = 2\) (Shop):
\[\alpha_2(\text{Rainy}) = 0.4 \cdot \left(0.06 \cdot 0.7 + 0.24 \cdot 0.4\right) \\\\ = 0.4 \cdot (0.042 + 0.096) = 0.4 \cdot 0.138 = 0.0552\] \[\alpha_2(\text{Sunny}) = 0.3 \cdot \left(0.06 \cdot 0.3 + 0.24 \cdot 0.6\right) \\\\ = 0.3 \cdot (0.018 + 0.144) = 0.3 \cdot 0.162 = 0.0486\]At \(t = 3\) (Clean):
\[\alpha_3(\text{Rainy}) = 0.5 \cdot \left(0.0552 \cdot 0.7 + 0.0486 \cdot 0.4\right) \\\\ = 0.5 \cdot (0.03864 + 0.01944) = 0.5 \cdot 0.05808 = 0.02904\] \[\alpha_3(\text{Sunny}) = 0.1 \cdot \left(0.0552 \cdot 0.3 + 0.0486 \cdot 0.6\right) \\\\ = 0.1 \cdot (0.01656 + 0.02916) = 0.1 \cdot 0.04572 = 0.004572\]Step 3: Likelihood of the observation sequence
\[P(x_1, x_2, x_3) = \alpha_3(\text{Rainy}) + \alpha_3(\text{Sunny}) = 0.02904 + 0.004572 = 0.033612\]Backward Pass
Let \(\beta_t(i)\) be the probability of observing the future sequence given state \(i\) at time \(t\).
Step 1: Initialization
\[\beta_3(\text{Rainy}) = \beta_3(\text{Sunny}) = 1\]Step 2: Recursion
At \(t = 2\) (next is Clean):
\[\beta_2(\text{Rainy}) = 0.7 \cdot 0.5 \cdot 1 + 0.3 \cdot 0.1 \cdot 1 = 0.35 + 0.03 = 0.38\] \[\beta_2(\text{Sunny}) = 0.4 \cdot 0.5 \cdot 1 + 0.6 \cdot 0.1 \cdot 1 = 0.20 + 0.06 = 0.26\]At \(t = 1\) (next is Shop):
\[\beta_1(\text{Rainy}) = 0.7 \cdot 0.4 \cdot 0.38 + 0.3 \cdot 0.3 \cdot 0.26 = 0.1064 + 0.0234 = 0.1298\] \[\beta_1(\text{Sunny}) = 0.4 \cdot 0.4 \cdot 0.38 + 0.6 \cdot 0.3 \cdot 0.26 = 0.0608 + 0.0468 = 0.1076\]Posterior Marginals
Now, compute the posterior probability of being in each state at each time:
At \(t = 1\)
\[P(z_1 = \text{Rainy} \mid x) = \frac{\alpha_1(\text{Rainy}) \cdot \beta_1(\text{Rainy})}{P(x)} = \frac{0.06 \cdot 0.1298}{0.033612} \approx 0.2317\] \[P(z_1 = \text{Sunny} \mid x) = \frac{0.24 \cdot 0.1076}{0.033612} \approx 0.7683\]And similarly for \(t = 2, 3\) using:
\[P(z_t = i \mid x) = \frac{\alpha_t(i) \cdot \beta_t(i)}{\sum_j \alpha_t(j) \cdot \beta_t(j)} = \frac{\alpha_t(i) \cdot \beta_t(i)}{P(x)}\]- The forward pass calculates the probability of partial sequences and helps estimate the likelihood of the entire sequence.
- The backward pass helps incorporate information from the future.
- Their combination gives us posterior marginals, i.e., probabilities of being in each state at each time.
- This is useful for smoothing, inference, and training HMMs via Expectation-Maximization.
Viterbi Decoding
While the forward-backward algorithm gives us the probability of being in a certain state at a certain time (marginal probabilities), what if we wanted to find the single most probable sequence of hidden states that could have generated the observation sequence? This is where Viterbi decoding comes in.
Think of it this way: imagine listening to a garbled sentence and trying to guess the exact original sentence that most likely produced those sounds. The Viterbi algorithm does something similar—it finds the path through the hidden states that maximizes the joint probability of the hidden sequence and the observations.
Formally, given an observation sequence \(x = (x_1, x_2, ..., x_T)\) and a Hidden Markov Model, the goal is to find the hidden state sequence \(z = (z_1, z_2, ..., z_T)\) that maximizes:
\[P(z_1, z_2, ..., z_T \mid x_1, x_2, ..., x_T)\]Or equivalently, since the denominator is constant:
\[\arg\max_{z_1, ..., z_T} P(z_1, ..., z_T, x_1, ..., x_T)\]The Viterbi algorithm uses dynamic programming to avoid enumerating all possible state sequences. It keeps track of the maximum probability of any path that ends in state j at time t, and then backtracks to recover the full sequence.
Let:
\[\delta_t(j) = \max_{z_1, ..., z_{t-1}} P(z_1, ..., z_{t-1}, z_t = j, x_1, ..., x_t)\]Then:
-
Initialization: \(\delta_1(j) = \pi_j \cdot B_j(x_1)\)
-
Recursion: \(\delta_t(j) = B_j(x_t) \cdot \max_i (\delta_{t-1}(i) A_{ij})\)
-
Backtrace: Track \(\psi_t(j)\) to reconstruct the path.
Viterbi Example
To better understand how the Viterbi algorithm works in practice, let’s apply it to the same example we used for the forward-backward algorithm. Our goal is different now: we’re not interested in the overall likelihood of the observations or marginal state probabilities. Instead, we want to find the single most likely sequence of hidden states that could have produced the observation sequence.
This is the decoding task: based on observed behaviors like “Walk”, “Shop”, and “Clean”, what is the most probable sequence of weather conditions (Rainy/Sunny) that explains them? We’ll follow the dynamic programming approach of Viterbi to solve this efficiently.
Step 1: Initialization
\[\delta_1(Rainy) = 0.6 \cdot 0.1 = 0.06 \\ \delta_1(Sunny) = 0.4 \cdot 0.6 = 0.24\]Step 2: Recursion
\[\delta_2(Rainy) = 0.4 \cdot \max(0.06 \cdot 0.7, 0.24 \cdot 0.4) = 0.4 \cdot \max(0.042, 0.096) = 0.4 \cdot 0.096 = 0.0384\] \[\delta_2(Sunny) = 0.3 \cdot \max(0.06 \cdot 0.3, 0.24 \cdot 0.6) = 0.3 \cdot 0.144 = 0.0432\]Step 3: Recursion at \(t = 3\)
We now use the outputs from step 2 to compute the most likely path to each state at time 3, given the third observation is “Clean”.
\[\delta_3(\text{Rainy}) = 0.5 \cdot \max(0.0384 \cdot 0.7, 0.0432 \cdot 0.4) \\ = 0.5 \cdot \max(0.02688, 0.01728) = 0.5 \cdot 0.02688 = 0.01344\] \[\delta_3(\text{Sunny}) = 0.1 \cdot \max(0.0384 \cdot 0.3, 0.0432 \cdot 0.6) \\ = 0.1 \cdot \max(0.01152, 0.02592) = 0.1 \cdot 0.02592 = 0.002592\]We now have the final deltas:
- \[\delta_3(\text{Rainy}) = 0.01344\]
- \[\delta_3(\text{Sunny}) = 0.002592\]
Step 4: Backtrace
Start from the state at \(t = 3\) with the highest \(\delta_3\):
\[\hat{z}_3 = \arg\max(\delta_3(Rainy), \delta_3(Sunny)) = \text{Rainy}\]Using the stored backpointers from the earlier steps (typically tracked in a table ( \psi )), we backtrack to recover the most probable state path.
Most likely state sequence:
\[[\text{Sunny}, \text{Rainy}, \text{Rainy}]\]Final interpretation: the most probable weather sequence that explains [Walk, Shop, Clean] is that it started Sunny, turned Rainy, and stayed Rainy.
This example illustrates two fundamentally different goals when working with Hidden Markov Models—and how two algorithms, though related, approach these goals differently.
The forward-backward algorithm is about uncertainty. It calculates the total probability of the observed sequence by summing over all possible hidden state paths. At each time step, it also gives us a soft assignment: the marginal probability of the model being in a specific state at that time. This is useful when we want a probabilistic understanding of what might have happened—like asking, “What is the likelihood it was Sunny on day 2, given everything I saw?”
In contrast, the Viterbi algorithm is about certainty. It doesn’t care about all possible paths—just the one best explanation. It finds the single most probable sequence of hidden states that could have generated the observations. This is especially useful when you want a definite decision—like tagging a sentence with one specific part-of-speech sequence or predicting the most likely user journey in a system.
So while forward-backward gives us a complete probabilistic picture, Viterbi gives us the most confident guess. Understanding this distinction is crucial for choosing the right approach depending on whether your downstream task needs probability distributions or concrete predictions.
Markov Chain Monte Carlo (MCMC)
As we move from modeling sequences to doing inference in probabilistic models, we run into a core problem: computing posteriors is often intractable.
Suppose you’re working with a complex probabilistic model where direct sampling or marginalizing over latent variables is impossible due to the sheer number of possible combinations. This happens frequently in Bayesian inference, where we want to compute posterior distributions of hidden parameters given observed data.
This is where Markov Chain Monte Carlo (MCMC) methods shine. They let us approximate complex distributions by simulating samples from them—even when those distributions can’t be written down explicitly or integrated analytically.
What is MCMC?
At a high level, MCMC methods do the following:
- Construct a Markov chain over a set of states (samples), with a carefully designed transition mechanism.
- Ensure the chain has a stationary distribution that matches the target posterior we want to approximate.
- Run the chain long enough so that samples from it behave like samples from the true posterior.
This is sampling via simulation—not exact, but often the best we can do in high-dimensional settings.
Let’s formalize it a bit.
Suppose we want to sample from a distribution \(p(x)\) which we only know up to a normalizing constant:
\[\tilde{p}(x) = \frac{1}{Z} p(x)\]We construct a Markov chain with transition kernel \(T(x' \mid x)\) such that:
- The chain is ergodic: it eventually explores the entire state space.
- The stationary distribution of the chain is \(p(x)\).
If we run the chain for many steps, and then sample from it (after a burn-in period), those samples approximate the target distribution.
Why Markov Chains?
Why use Markov chains at all?
Because they give us a way to construct dependent samples that converge toward a desired distribution. We no longer need to know how to directly draw from \(p(x)\). We only need to design transitions that are:
- Easy to compute
- Respect detailed balance
- Lead to the right long-run behavior (i.e., stationary distribution)
Interpreting MCMC Through Examples
Let’s walk through a few intuitive examples to understand how MCMC operates in practice.
Example 1: Sampling from a Posterior You Can’t Normalize
Suppose you’re a data scientist trying to model customer churn using a Bayesian logistic regression. You specify a prior for your model weights and define a likelihood function. However, the resulting posterior distribution is complex and not analytically integrable.
Using MCMC, you simulate a long chain of weight vectors. The early samples (burn-in) help the chain explore the space. Later samples represent plausible sets of parameters. You can now:
- Visualize uncertainty over each weight (e.g., how strongly income predicts churn)
- Make probabilistic predictions by averaging across many samples
This is especially valuable when decision thresholds matter (e.g., setting interest rates based on risk).
Example 2: Exploring Multi-modal Distributions
Imagine a model where the posterior has two separate peaks—for example, detecting two potential clusters in fraud patterns. Traditional optimization might just return one peak (the mode), but MCMC gives you samples from both regions, allowing you to:
- Discover both fraud strategies
- Quantify how much probability mass lies in each
Example 3: Intuition Through a Board Game
Think of trying to explore a dark room with only a flashlight. Each move you make is like proposing a new state in MCMC. If the room is a weird shape (i.e., the posterior distribution is irregular), you won’t just jump randomly—you’ll use feedback (accept/reject steps) to guide your path.
Over time, if your steps are designed right, you’ll spend more time in regions of the room with more interesting structure—just like how MCMC spends more time in high-probability regions.
These examples highlight why MCMC is not just a math tool—it’s a general framework for reasoning under uncertainty and approximating the uncomputable.
Where Does This Help?
This is especially useful in Bayesian models with latent variables or large parameter spaces.
For example:
- In topic modeling (e.g., LDA), we sample topic assignments for words.
- In probabilistic graphical models, we infer hidden node values.
- In HMMs, we can use MCMC to sample hidden state trajectories conditioned on observations.
It’s also the engine behind Bayesian deep learning, Gaussian process inference, and posterior predictive checks.
Next, we’ll get concrete with two powerful MCMC algorithms: Gibbs Sampling and Metropolis-Hastings.
Metropolis-Hastings Algorithm
Why It Matters
Often in data science, we need to sample from a complex probability distribution. We might know the unnormalized density (like the posterior in Bayesian models) but can’t sample directly. Metropolis-Hastings (MH) gives us a general-purpose way to explore these spaces.
Imagine having a rugged landscape where height = probability. MH helps you walk around this terrain and sample points proportionally to how high they are.
The Core Idea
Construct a Markov chain whose stationary distribution is the target distribution \(p(x)\).
Step-by-Step Algorithm
We want to sample from a distribution \(p(x)\) which we only know up to a constant:
\(p(x) = \frac{1}{Z} \tilde{p}(x)\)
but we can compute \(\tilde{p}(x)\).
1. Initialize
Choose an initial point \(x^{(0)}\).
2. Propose a new sample
Use a proposal distribution:
\(x' \sim q(x' \mid x^{(t)})\)
3. Compute the acceptance probability
\[\alpha = \min\left(1, \frac{\tilde{p}(x') \cdot q(x^{(t)} \mid x')}{\tilde{p}(x^{(t)}) \cdot q(x' \mid x^{(t)})}\right)\]4. Accept or reject
- With probability \(\alpha\), set \(x^{(t+1)} = x'\)
- Otherwise, \(x^{(t+1)} = x^{(t)}\)
Repeat for many iterations.
Numerical Example: 1D Gaussian Target
Let’s say our target is:
\(p(x) \propto \exp\left(-\frac{(x - 3)^2}{2}\right)\)
It’s a Normal(3, 1), but we pretend we don’t know how to sample from it directly.
Let’s use a simple Gaussian proposal:
\(q(x' \mid x) = \mathcal{N}(x, 1)\)
Start at \(x^{(0)} = 0\).
- Propose \(x' = 2.5\)
- Compute:
Proposal is symmetric, so:
\[\alpha = \min\left(1, \frac{0.8825}{0.0111} \right) = 1\]→ Accept.
Set \(x^{(1)} = 2.5\).
Repeat this process. Over time, the histogram of samples will match \(\mathcal{N}(3, 1)\).
Why Metropolis-Hastings Works
Because we define a Markov Chain that has the target distribution as its stationary distribution, and the accept/reject step ensures detailed balance:
\[\pi(x) T(x \to x') = \pi(x') T(x' \to x)\]Gibbs Sampling
When to Use It
Gibbs Sampling is a special case of MH when:
- We have multivariate distributions
- We can’t sample from the joint, but can sample from the conditional distributions
Core Idea
Cycle through dimensions and sample each one conditioned on all the others.
Suppose: \(p(x, y) \text{ is complex, but } p(x \mid y) \text{ and } p(y \mid x) \text{ are easy}\)
Numerical Example: Bivariate Normal
We want to sample from:
\[\begin{bmatrix} x \\ y \end{bmatrix} \sim \mathcal{N}\left( \begin{bmatrix} 0 \\ 0 \end{bmatrix}, \begin{bmatrix} 1 & 0.8 \\\\ 0.8 & 1 \end{bmatrix} \right)\]It has high correlation — like two variables moving together.
From properties of multivariate Gaussians, the conditionals are:
- \[x \mid y \sim \mathcal{N}(0.8y, 0.36)\]
- \[y \mid x \sim \mathcal{N}(0.8x, 0.36)\]
Start with \(x^{(0)} = 0\), \(y^{(0)} = 0\)
Step 1: Sample \(x^{(1)}\) given \(y^{(0)} = 0\)
\[x^{(1)} \sim \mathcal{N}(0.8 \cdot 0, 0.36) = \mathcal{N}(0, 0.36)\]Suppose you get \(x^{(1)} = 0.3\)
Step 2: Sample \(y^{(1)}\) given \(x^{(1)} = 0.3\)
\[y^{(1)} \sim \mathcal{N}(0.8 \cdot 0.3, 0.36) = \mathcal{N}(0.24, 0.36)\]Suppose you get \(y^{(1)} = 0.1\)
Repeat for many steps. Your samples will form a correlated elliptical cloud.
Why Gibbs Works
Each conditional update defines a Markov chain. Under mild conditions (irreducibility, aperiodicity), the chain converges to the joint distribution.
Applications in Data Science
- Bayesian Networks: You can Gibbs sample from graphical models.
- Topic Modeling: In Latent Dirichlet Allocation (LDA), Gibbs sampling is used to assign topics to words.
- Image Denoising: Pixel intensities conditioned on neighbors.
Summary
| Method | When to Use | Pros | Cons |
|---|---|---|---|
| Metropolis-Hastings | General-purpose MCMC | Flexible | Can reject proposals often |
| Gibbs Sampling | When conditionals are tractable | Always accepts | Needs access to all conditionals |
Sure! Here’s a natural, storytelling-style introduction to your visualizations, written in a voice that matches the rest of your blog. You can place this section just before the figures:
Visualizing the Sampling Process
It’s one thing to understand Metropolis-Hastings and Gibbs Sampling through equations. But what do these algorithms actually look like in motion? How do they explore the probability space? How do their behaviors differ?
Let’s bring them to life with visualizations.
To make things concrete, we simulated two classic cases:
- A 1D Gaussian distribution for Metropolis-Hastings
- A bivariate Gaussian with strong correlation for Gibbs Sampling
The goal was simple: visualize how each algorithm moves through its state space, how it generates samples, and what patterns emerge over time.
You’ll see how Metropolis-Hastings occasionally rejects steps and how Gibbs Sampling zig-zags through dimensions—an intuitive look at what makes these algorithms tick under the hood.
Now, let’s walk through the visual evidence.
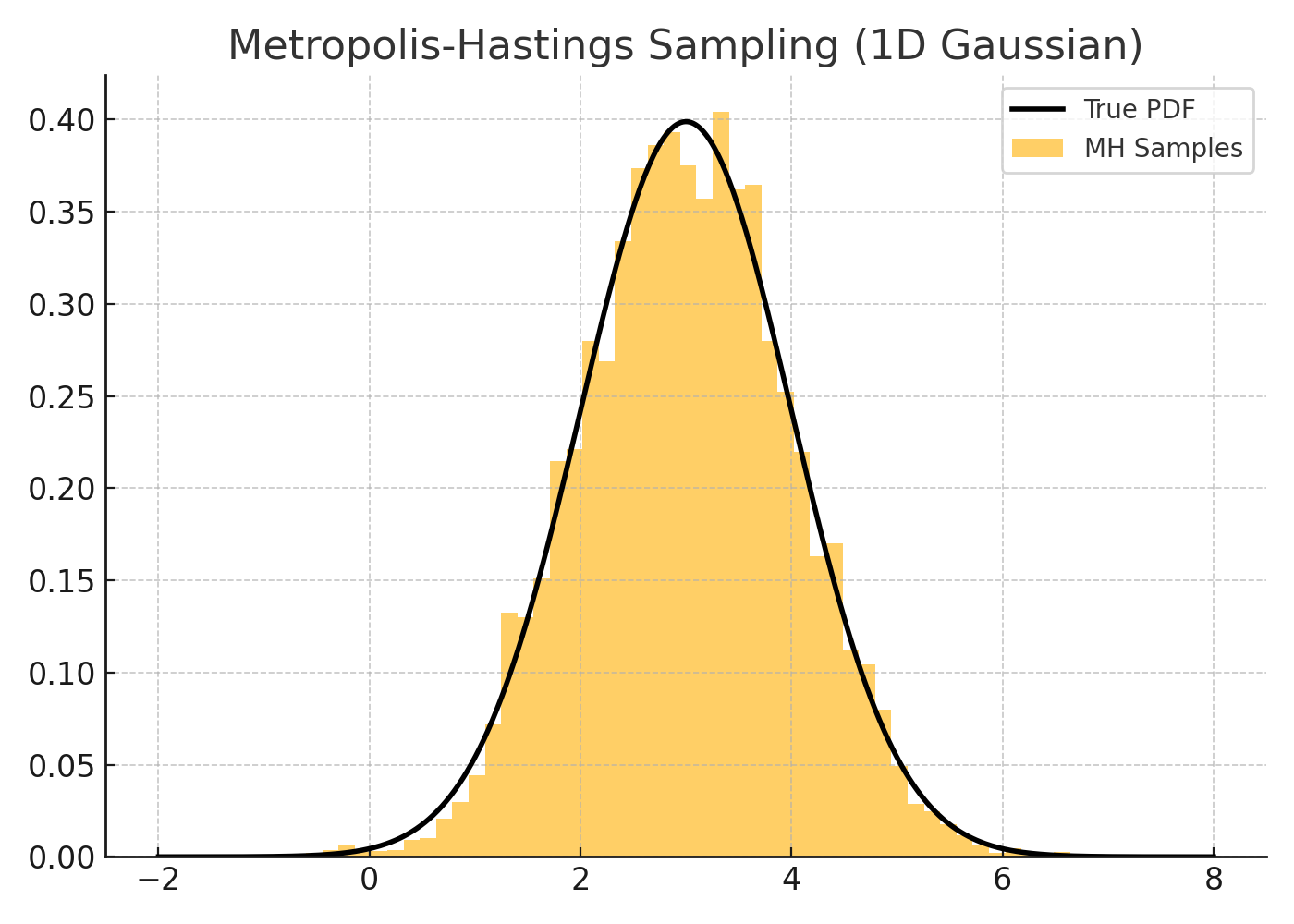
This figure compares the distribution of samples generated by the Metropolis-Hastings algorithm (blue histogram) against the true probability density function (black curve) of a 1D Gaussian centered at 3.
- The histogram closely follows the curve, showing that MH sampling converged correctly.
- The proposal distribution was Gaussian, and enough steps ensured good mixing.
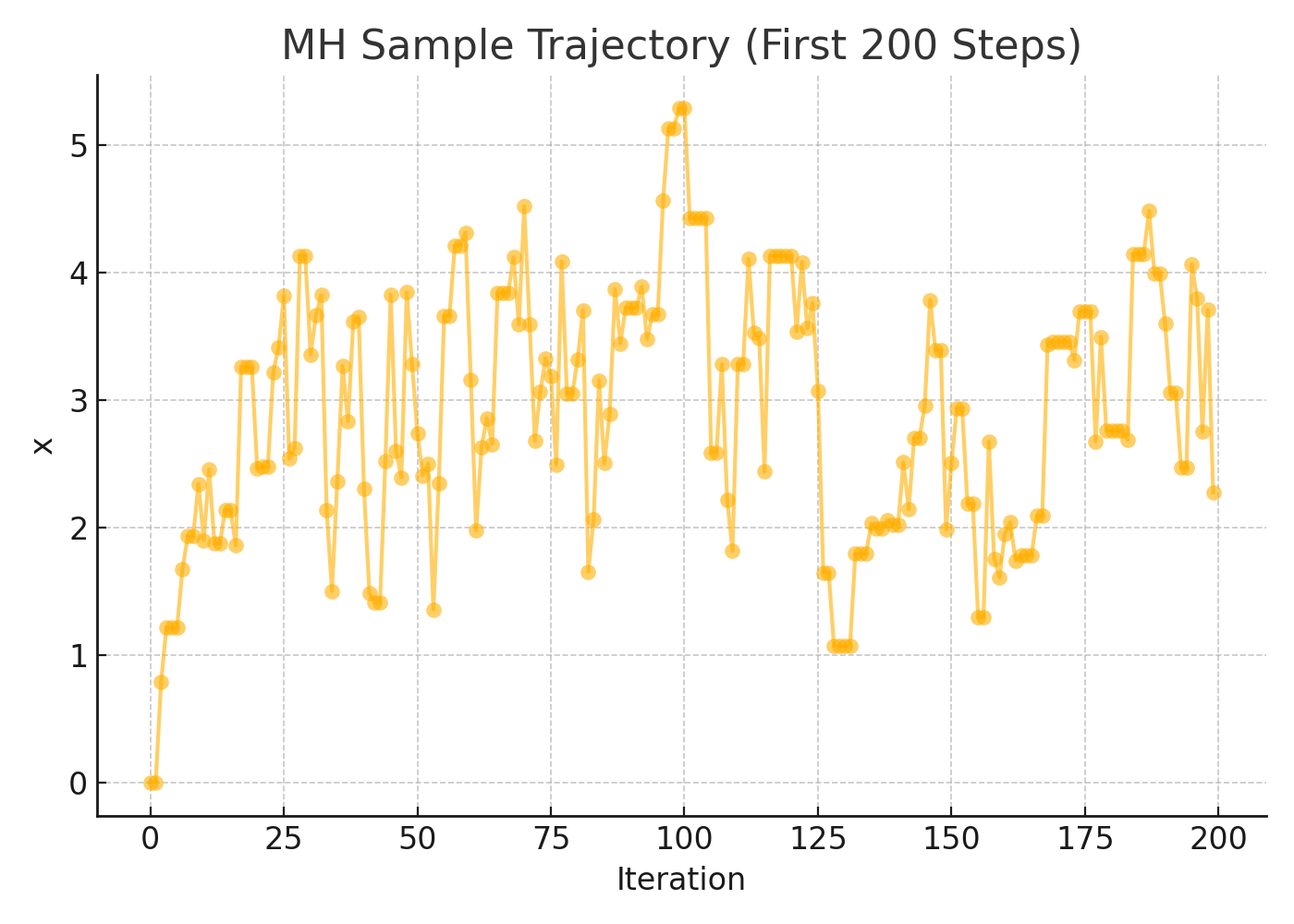
This plot shows how the sampled value evolves over time (first 200 steps). It starts at 0 and moves toward the high-density region near 3.
- Early steps move quickly—MH is exploring the space.
- Plateaus in the line indicate rejected proposals, where the chain stays put.
- This trace helps check mixing and convergence.
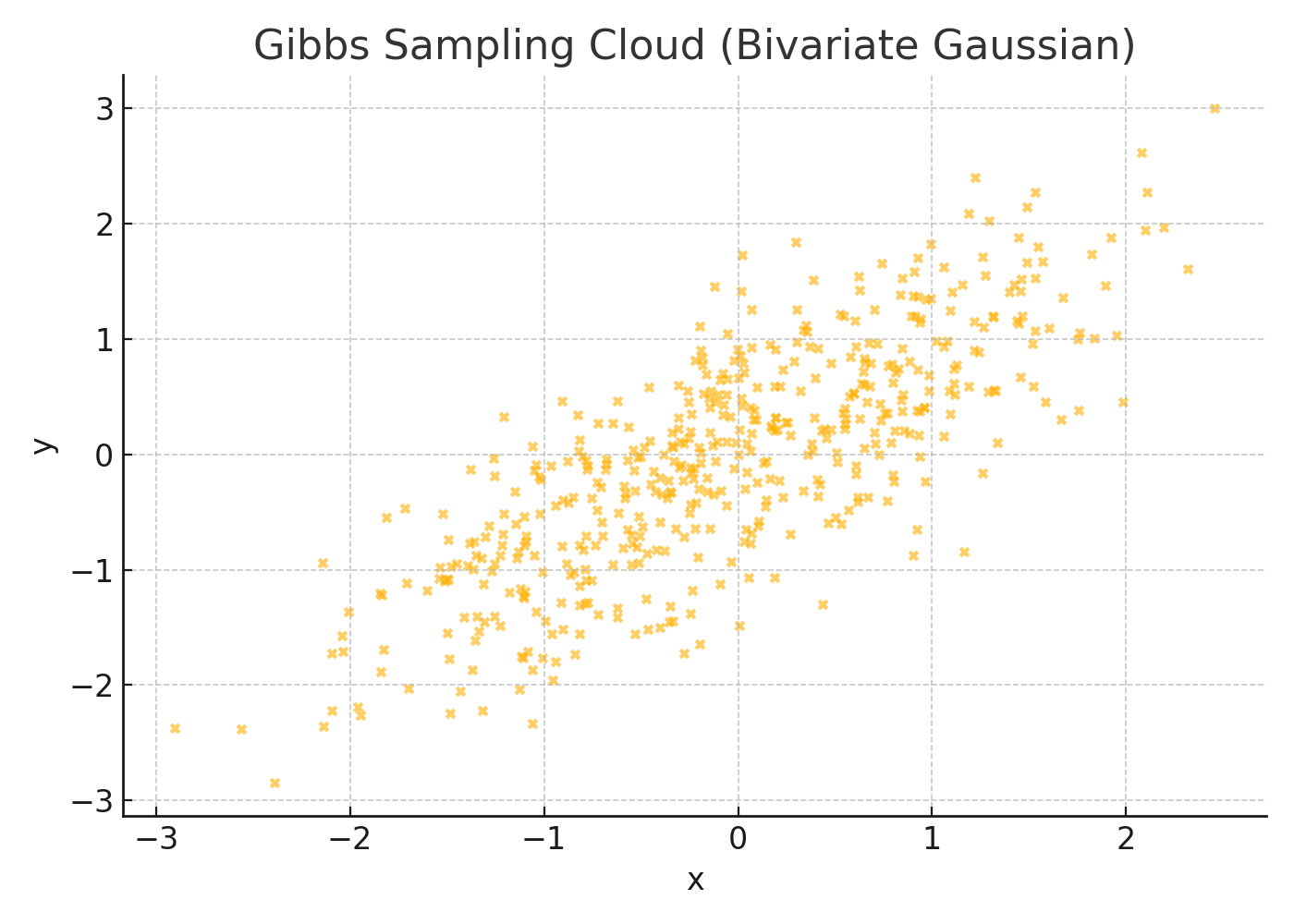
This scatter plot shows samples drawn using Gibbs sampling from a bivariate normal distribution with high correlation (ρ = 0.8).
- The elliptical shape reflects the true correlation between the variables.
- This cloud is what we expect if Gibbs converges properly to the joint distribution.
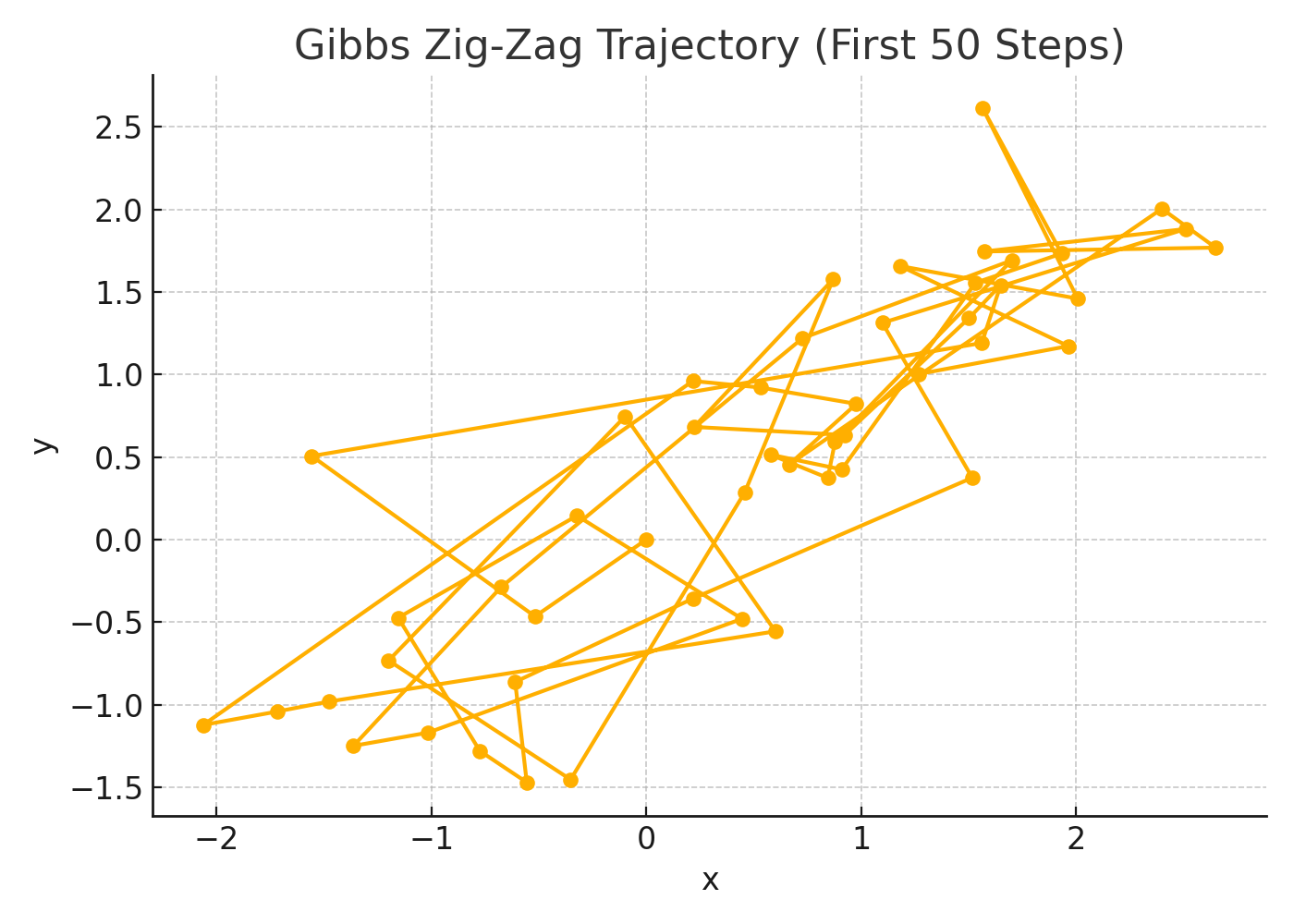
This plot tracks the path of the sampler during the first 50 iterations.
- Gibbs updates one variable at a time, creating a stair-step / zig-zag path.
- This behavior is unique to Gibbs and is ideal when conditionals are known.
Markov Decision Processes (MDPs): Modeling Decision-Making Over Time
Up to now, we’ve talked about modeling uncertainty—whether through state transitions in Markov chains, latent dynamics in HMMs, or posterior distributions in Bayesian inference via MCMC. But what if you’re not just observing a system—you’re interacting with it?
This is where Markov Decision Processes come in.
Where It Begins: Not Just Probabilities, But Choices
Imagine you’re a robot in a grid world. At each step, you can move north, south, east, or west. The environment is stochastic—there’s wind, obstacles, even sudden teleportation. Your goal is to get to a charging station with minimal battery drain.
Every decision you make affects what happens next. And each outcome has a consequence.
MDPs let us formally describe this type of sequential decision-making under uncertainty.
The Formal Ingredients of an MDP
An MDP is defined by a 5-tuple:
\[\text{MDP} = (S, A, P, R, \gamma)\]Where:
- \(S\): A finite set of states
- \(A\): A finite set of actions
- \(P(s' \mid s, a)\): The transition probability of reaching state \(s'\) from state \(s\) when taking action \(a\)
- \(R(s, a)\): The reward received after taking action \(a\) in state \(s\)
- \(\gamma\): The discount factor, with \(0 \leq \gamma < 1\), which downweights future rewards
What’s the Goal?
Find a policy:
\[\pi: S \rightarrow A\]That maps each state to an action to maximize the expected long-term reward:
\[V^\pi(s) = \mathbb{E}\left[\sum_{t=0}^{\infty} \gamma^t R(s_t, a_t) \mid s_0 = s, \pi \right]\]The optimal policy \(\pi^*\) satisfies:
\[\pi^* = \arg\max_\pi V^\pi(s)\]Insight: The Markov Property Again
Note how this builds on our earlier idea—the Markov property still holds. The next state depends only on the current state and action, not the full history.
But now we’ve added:
- Control (actions)
- Goals (rewards)
Examples in Data Science
- Recommendation systems: MDPs can model how users interact over time with a platform (e.g., clicking, skipping, purchasing). Each action (recommendation) influences future user state.
- Dynamic pricing: Retailers adjust prices based on customer behavior and inventory over time to optimize revenue.
- Healthcare: Choosing treatment plans that optimize long-term patient outcomes under uncertainty.
- Credit line management: Banks adjust credit limits dynamically to minimize risk and maximize profit.
Connection to Reinforcement Learning
If MDPs are the theory, reinforcement learning (RL) is the practice.
In RL, you don’t know the transition probabilities or rewards upfront. You interact with the environment and learn a good policy by trial and error—using algorithms like Q-learning, Policy Gradients, or Actor-Critic methods.
But behind it all: the structure is always an MDP.
Applications in Practice
Let’s now see how all these mathematical tools—Markov chains, HMMs, MCMC, MDPs—are used in the wild.
Part-of-Speech (POS) Tagging
Task: Assign a grammatical label (noun, verb, adjective, etc.) to every word in a sentence.
Example:
“The cat sat on the mat”
→ [Det, Noun, Verb, Prep, Det, Noun]
Why it’s hard:
- Words are ambiguous (“flies” can be noun or verb)
- Context matters
- There’s sequential dependency
How it uses HMMs:
- Hidden states = POS tags
- Observations = words
- Emissions = word probabilities given tags
- Transitions = tag-to-tag probabilities
Using the Viterbi algorithm, we decode the most likely tag sequence given the words.
Here’s how HMM-based POS tagging compares to more modern methods:
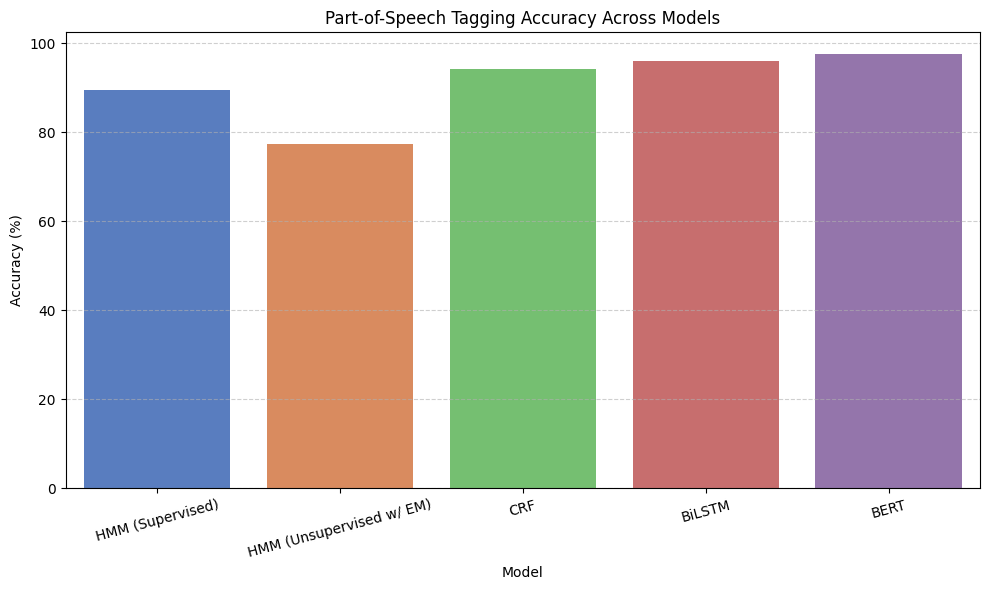
Key Takeaway: Even today, HMMs form the foundation of sequence modeling pipelines—especially in low-resource settings or when interpretability matters.
Speech Recognition
In automatic speech recognition (ASR), the task is to map a continuous waveform to a sequence of words.
The basic HMM-based pipeline looks like:
- Acoustic Model
- Models the likelihood of sounds (phonemes) given a word
- Often modeled as Gaussian Mixture Models (GMMs) or HMMs over feature vectors like MFCCs
- Language Model
- A Markov model over words:
\(P(w_1, w_2, ..., w_T) = \prod_{t=1}^T P(w_t \mid w_{t-1})\)
- A Markov model over words:
- Decoding
- Combine the acoustic and language models using Viterbi to find the most probable word sequence.
Even with deep learning, hybrid HMM-DNN models were dominant for a long time—and the decoder is still often Viterbi-like.
Bayesian Inference Using Sampling
Let’s say you’re doing fraud detection, and you’ve modeled transaction features using a probabilistic graphical model. You want to know:
“Given all this messy, sparse, non-convex evidence, what’s the probability that this transaction is fraudulent?”
Here’s where MCMC shines.
- Complex posteriors (due to multiple latent variables and dependencies)
- No closed-form posterior
- Sampling methods like Gibbs or Metropolis-Hastings give you a way to approximate the posterior
You can then:
- Compute credible intervals
- Visualize uncertainty
- Run posterior predictive checks
In Bayesian regression, topic models, hierarchical models—sampling is often the only tractable inference method.
Reinforcement Learning (RL)
At the heart of every RL problem is an MDP.
In game-playing agents, robots, and even recommendation systems:
- The environment is an MDP
- The agent takes actions and gets rewards
- The goal is to learn an optimal policy via trial-and-error
Classic algorithms like Q-learning, SARSA, and Policy Gradient methods all rely on the structure of MDPs. And yes—every time we estimate transition dynamics or sample trajectories, we are implicitly doing Markov Chain simulation.
Time Series and Sequence Modeling
Sequence data is everywhere:
- Stock prices
- Web traffic
- Medical measurements
- Sensor readings
- Language, DNA, and behavior logs
And nearly every probabilistic model of these sequences:
- Assumes Markov structure
- Uses HMMs or autoregressive chains
- Learns transition matrices, emission distributions, or latent dynamics
When time is involved, Markovian assumptions are often the first modeling layer.
Conclusion: A Markovian Mindset
What began with a Russian mathematician analyzing poetry has become a universal way to think about sequences, structure, and uncertainty.
Markov models help us:
- Simplify sequential dependencies
- Infer hidden causes
- Sample from uncertainty
- Make decisions in dynamic environments
Whether you’re tagging parts of speech, modeling speech signals, approximating Bayesian posteriors, or building intelligent agents—the same foundational ideas echo underneath.
So the next time you’re solving a data science problem involving time, structure, or uncertainty—ask yourself:
“Is there a Markov assumption I can make?”
Chances are, you’ll find not just an assumption—but a solution.