Multivariable Functions & Gradients
- Functions of Several Variables
- Partial vs. Total Derivatives
- Gradient Vector: \(\nabla f(x)\)
- Critical Points and Optima
- Finding Minima Using Gradients
- Directional Derivatives and Steepest Descent
- Level Sets and Contour Plots for Loss Surfaces
- Jacobian Matrix: Shape, Interpretation, and When It Matters
- Hessian Matrix: Curvature, Convexity, and Second-Order Conditions
- Classifying Critical Points Using the Hessian
- Applications
- Wrapping Up
Before a neural network can learn, before a model loss can be minimized, and before gradients can flow through layers—there’s one quiet foundational idea beneath it all:
Functions of many variables.
In school, we learn functions like \(f(x) = x^2\) or \(g(x) = \sin(x)\)—clean, one-dimensional stories. But data science doesn’t live in one dimension. Our models don’t take a single input. Our loss functions don’t live on a line.
Instead, machine learning is built on top of functions that eat whole vectors:
\[f(x_1, x_2, \dots, x_n)\]If you’re training a model, the loss might depend on a thousand weights. It’s no longer a curve—it’s a surface. Or worse: a terrain in 10,000-dimensional space.
And to move toward a minimum, we need to ask questions like:
- Which direction should we move? (that’s the gradient)
- How fast should we move? (that’s the gradient magnitude)
- What does the terrain look like nearby? (enter the Hessian)
Let’s start from the ground up.
Functions of Several Variables
Suppose you’re training a regression model with two features, \(x_1\) and \(x_2\). A typical loss function might look like:
\[f(x_1, x_2) = x_1^2 + 4x_2^2\]This function takes two inputs and produces a single output—it maps \(\mathbb{R}^2 \rightarrow \mathbb{R}\). Visually, this defines a smooth surface: a 3D bowl where the lowest point represents the minimum loss.
Let’s visualize what this surface looks like. Here’s how it behaves as we tweak \(x_1\) and \(x_2\):
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
x1 = np.linspace(-5, 5, 100)
x2 = np.linspace(-5, 5, 100)
X1, X2 = np.meshgrid(x1, x2)
Z = X1**2 + 4*X2**2
fig = plt.figure(figsize=(8,6))
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(X1, X2, Z, cmap='viridis')
ax.set_xlabel('x1')
ax.set_ylabel('x2')
ax.set_zlabel('f(x1, x2)')
plt.title('f(x1, x2) = x1² + 4x2²')
plt.show()
What we’re seeing here is a quadratic bowl. Imagine dropping a ball onto the surface—it’ll roll toward the lowest point. The way it moves is shaped by the slope, direction, and curvature of the surface. That movement—how functions change as inputs vary—is what we’ll now study using derivatives.
Let’s start with partial derivatives.
Partial vs. Total Derivatives
In single-variable calculus, we use the derivative:
\[\frac{df}{dx}\]But for multivariable functions, we need to ask: which direction are we moving? Are we changing just one variable, or several?
Partial Derivatives
A partial derivative measures the rate of change of a function with respect to one variable, while holding the others fixed.
For our function:
\[f(x_1, x_2) = x_1^2 + 4x_2^2\]We compute:
\[\frac{\partial f}{\partial x_1} = 2x_1\] \[\frac{\partial f}{\partial x_2} = 8x_2\]These partial derivatives tell us how steep the function is in the \(x_1\) and \(x_2\) directions independently.
Later on, we’ll stack these partials into a gradient vector to find the overall direction of steepest ascent or descent.
Total Derivatives
Partial derivatives are local—one direction at a time. But in many real situations, inputs change together.
Suppose:
\[x_1(t) = t, \quad x_2(t) = t^2\]Then:
\[f(t) = f(x_1(t), x_2(t)) = x_1^2 + 4x_2^2 = t^2 + 4t^4\]To compute how \(f\) evolves with time:
\[\frac{df}{dt} = \frac{\partial f}{\partial x_1} \cdot \frac{dx_1}{dt} + \frac{\partial f}{\partial x_2} \cdot \frac{dx_2}{dt}\]Compute each term:
- \[\frac{\partial f}{\partial x_1} = 2x_1 = 2t\]
- \[\frac{\partial f}{\partial x_2} = 8x_2 = 8t^2\]
- \[\frac{dx_1}{dt} = 1, \quad \frac{dx_2}{dt} = 2t\]
So:
\[\frac{df}{dt} = 2t \cdot 1 + 8t^2 \cdot 2t = 2t + 16t^3\]This total derivative tells us the rate at which the function changes as both inputs evolve over time—this idea becomes crucial in understanding how loss behaves during optimization when multiple parameters are updated together.
Gradient Vector: \(\nabla f(x)\)
Partial derivatives tell us how a function changes when we vary one input at a time. But in most real-world scenarios—especially in machine learning—we don’t move along just one axis. We move through parameter space, tweaking multiple variables simultaneously.
To navigate that space wisely, we need a direction that tells us where the function increases fastest. That direction is given by the gradient vector.
For a function \(f(x_1, x_2, \dots, x_n)\), the gradient is:
\[\nabla f(x) = \left[ \frac{\partial f}{\partial x_1},\ \frac{\partial f}{\partial x_2},\ \dots,\ \frac{\partial f}{\partial x_n} \right]^T\]This vector points in the direction of steepest ascent—where the function increases most rapidly. In optimization problems, especially in machine learning, we typically want to minimize a function, so we follow the negative gradient to move “downhill.”
Example
We have
\[f(x_1, x_2) = x_1^2 + 4x_2^2\]The gradient is:
\[\nabla f(x_1, x_2) = \begin{bmatrix} 2x_1 \\ 8x_2 \end{bmatrix}\]The function increases faster along the \(x_2\) axis than the \(x_1\) axis, due to the steeper curvature from the 4 multiplier.
Contour Visualization with Gradients
Let’s plot the contours of this function, and at each point, draw the gradient vector to show how the function behaves locally.
import numpy as np
import matplotlib.pyplot as plt
# Grid definition
x1 = np.linspace(-4, 4, 40)
x2 = np.linspace(-4, 4, 40)
X1, X2 = np.meshgrid(x1, x2)
# Function and gradient
Z = X1**2 + 4 * X2**2
df_dx1 = 2 * X1
df_dx2 = 8 * X2
grad_magnitude = np.sqrt(df_dx1**2 + df_dx2**2)
# Plot setup
plt.figure(figsize=(10, 8))
# Contour plot
contours = plt.contour(X1, X2, Z, levels=25, cmap='viridis')
plt.clabel(contours, inline=True, fontsize=9, fmt="%.0f")
# Gradient arrows with magnitude coloring
skip = (slice(None, None, 2), slice(None, None, 2)) # downsample for readability
quiver = plt.quiver(
X1[skip], X2[skip], df_dx1[skip], df_dx2[skip],
grad_magnitude[skip], cmap='inferno', scale=100, width=0.005
)
cb = plt.colorbar(quiver, label='Gradient Magnitude')
# Labels and aesthetics
plt.xlabel(r'$x_1$', fontsize=12)
plt.ylabel(r'$x_2$', fontsize=12)
plt.title(r'Contours and Gradient Field of $f(x_1, x_2) = x_1^2 + 4x_2^2$', fontsize=14)
plt.grid(True, linestyle='--', alpha=0.6)
plt.axis('equal')
plt.tight_layout()
plt.show()
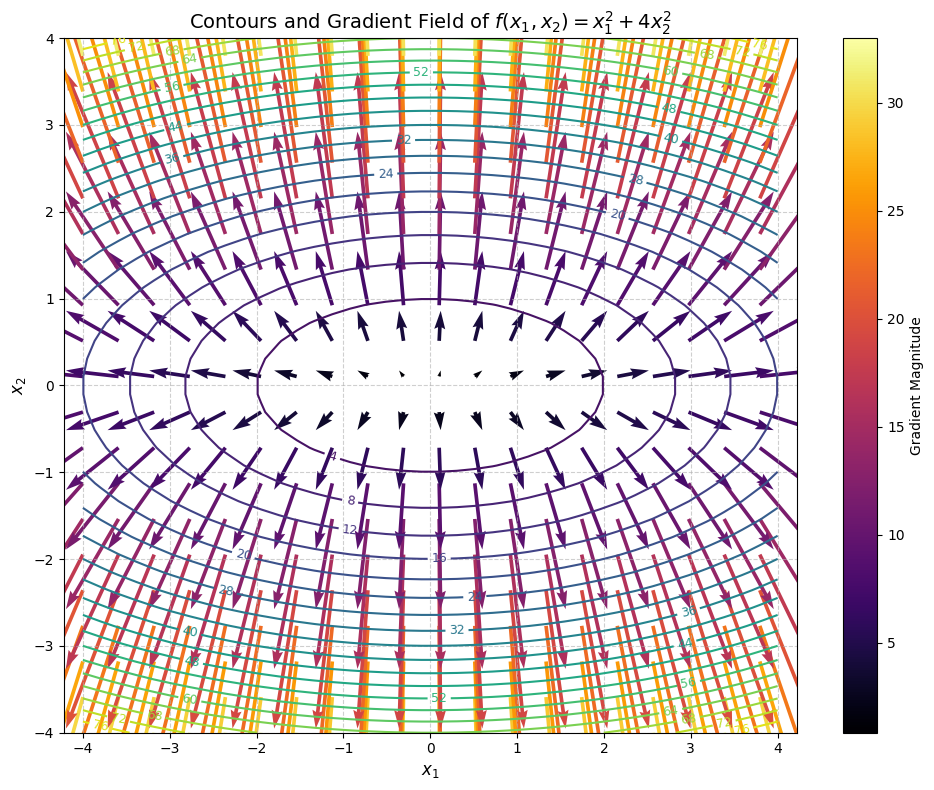
What you see in this plot are the elliptical contours of the function and a field of red arrows, each representing the gradient at that point. Notice how:
- The arrows grow longer farther from the origin—indicating steeper slopes.
- They are perpendicular to the contour lines—because the gradient always points orthogonally to level sets.
- Near the minimum at the origin, the gradient vanishes—the function is flat.
This is not just mathematical trivia; it’s the very geometry of optimization. When we use gradient descent, we move against the gradient to descend the surface toward a minimum:
\[\theta^{(t+1)} = \theta^{(t)} - \eta \cdot \nabla f(\theta^{(t)})\]The learning rate \(\eta\) controls how far we step, but the direction is always determined by \(\nabla f\).
Critical Points and Optima
Once we understand the gradient vector \(\nabla f(x)\), the natural question is: where does it vanish?
These locations—where the gradient becomes zero—are called critical points.
What Are Critical Points?
A critical point of a function is any point \(x\) where the gradient vector is zero:
\[\nabla f(x) = 0\]Intuitively, at a critical point, the function is locally “flat”—there’s no immediate slope pushing the function higher or lower. These points are where potential minima, maxima, or saddle points could occur.
In optimization, critical points are crucial: they’re the places where we might find the best (or worst) values of our objective function.
Finding Critical Points: A Simple Example
Let’s walk through a basic case.
Suppose:
\[f(x, y) = x^2 + y^2\]First, compute the gradient:
\[\nabla f(x, y) = \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix} = \begin{bmatrix} 2x \\ 2y \end{bmatrix}\]Now, to find the critical points, we set the gradient equal to zero:
\[\nabla f(x, y) = 0\]This gives the system:
\[2x = 0 \quad \text{and} \quad 2y = 0\]Solving this, we get:
\[x = 0, \quad y = 0\]Thus, the critical point is:
\[(x, y) = (0, 0)\]Setting the gradient to zero is a necessary condition for a point to be an extremum (minimum, maximum, or saddle point).
However, it’s not sufficient—not every critical point is a minimum or maximum.
For instance:
- Some critical points are local minima (lowest nearby values).
- Some are local maxima (highest nearby values).
- Others are saddle points, which are minima in one direction and maxima in another.
We’ll see how to classify them shortly when we introduce the Hessian.
Applications in Machine Learning
- Loss minimization: In linear regression, logistic regression, and deep learning, we minimize a loss function. The optimal weights correspond to critical points where the loss gradient vanishes.
- Training stability: In deep learning, understanding when gradients vanish (or explode) helps in designing better architectures (like ResNets) and choosing appropriate activations.
Every time you run gradient descent, you’re essentially trying to find a critical point where \(\nabla f(x) \approx 0\).
Finding Minima Using Gradients
After identifying critical points by setting \(\nabla f(x) = 0\), the next question is: how do we actually reach these points in practice?
In most real-world problems—especially in machine learning—we aren’t handed the critical point on a silver platter. We need an algorithm to find it.
This is where gradient descent comes in.
The Concept of Minimization
In machine learning, the goal of training models often boils down to minimizing a loss function.
- In linear regression, we minimize the mean squared error.
- In logistic regression, we minimize cross-entropy loss.
- In deep learning, we minimize increasingly complex loss functions designed for classification, generation, or prediction.
The idea is simple: find the parameter values that make the loss function as small as possible.
How Gradient Descent Works
Gradient descent is an iterative optimization algorithm.
Starting from an initial guess, it repeatedly updates the variables in the direction of steepest descent—that is, opposite to the gradient.
At each step:
\[\mathbf{x}_{\text{new}} = \mathbf{x} - \eta \nabla f(\mathbf{x})\]where:
- \(\mathbf{x}\) is the current point (parameter values),
- \(\nabla f(\mathbf{x})\) is the gradient at that point,
- \(\eta\) is the learning rate, a small positive scalar controlling the step size.
The gradient tells us which way is uphill—so moving in the opposite direction takes us downhill, closer to a minimum.
Numerical Demonstration: Simple 2D Function
Let’s revisit our simple function:
\[f(x, y) = x^2 + y^2\]Its gradient is:
\[\nabla f(x, y) = \begin{bmatrix} 2x \\ 2y \end{bmatrix}\]Suppose we start at:
\[(x, y) = (2, 3)\]and use a learning rate \(\eta = 0.1\).
First gradient step:
- Compute the gradient at (2, 3):
- Update:
Next steps would continue similarly—computing the gradient at the new point and updating again.
Each step brings us closer to the critical point (0, 0), which is the global minimum for this function.
Why Gradient Descent Works
At every iteration, gradient descent moves toward regions of lower function value.
The learning rate controls how aggressively we move:
- If \(\eta\) is too large, we might overshoot the minimum.
- If \(\eta\) is too small, convergence can be slow.
Choosing the right learning rate and using methods like momentum or adaptive learning rates (e.g., Adam) are key parts of training modern machine learning models.
Gradient descent is fundamental across ML:
- In linear regression, it finds the line (or hyperplane) that best fits the data.
- In logistic regression, it optimizes parameters to correctly classify data.
- In deep neural networks, it tunes millions of parameters to reduce training loss.
Every time a model “learns,” it’s really performing hundreds of thousands—or millions—of tiny gradient descent updates under the hood.
Directional Derivatives and Steepest Descent
We know that the gradient vector \(\nabla f(x)\) tells us the direction in which a function increases most rapidly. But what if we’re not moving exactly in that direction?
In many optimization problems, especially in constrained settings, we may be forced to move in a specific direction. Naturally, the question arises:
How fast does the function increase (or decrease) if I move in a particular direction?
This is where directional derivatives come in.
The Idea
Given a direction vector \(\mathbf{v}\), the directional derivative of a function \(f(x)\) at a point \(x\) in the direction of \(\mathbf{v}\) is defined as:
\[D_{\mathbf{v}} f(x) = \nabla f(x) \cdot \mathbf{v}\]This is the dot product between the gradient and the direction vector.
Geometrically, this measures the projection of the gradient onto \(\mathbf{v}\)—that is, how much of the gradient’s influence actually acts along the direction \(\mathbf{v}\).
A Simple Case
Let’s reuse the same function:
\[f(x_1, x_2) = x_1^2 + 4x_2^2\]We already know the gradient:
\[\nabla f(x_1, x_2) = \begin{bmatrix} 2x_1 \\ 8x_2 \end{bmatrix}\]Now suppose we want to compute the directional derivative at point \(x = (1, 1)\) in the direction:
\[\mathbf{v} = \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix}\](That is, moving diagonally northeast in 2D.)
Compute the gradient at that point:
\[\nabla f(1, 1) = \begin{bmatrix} 2 \\ 8 \end{bmatrix}\]Then:
\[D_{\mathbf{v}} f(1, 1) = \nabla f(1,1) \cdot \mathbf{v} = \begin{bmatrix} 2 \\ 8 \end{bmatrix} \cdot \frac{1}{\sqrt{2}} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = \frac{1}{\sqrt{2}}(2 + 8) = \frac{10}{\sqrt{2}} \approx 7.07\]So the function increases at a rate of about 7.07 per unit movement in that direction.
Why the Dot Product?
The dot product captures two things at once:
- The alignment between the gradient and your chosen direction: if you move perfectly in the gradient’s direction, you get the full steepness.
- The magnitude of the gradient: stronger gradients push the function value more rapidly.
This leads to a key observation:
The directional derivative is maximized when \(\mathbf{v}\) is perfectly aligned with \(\nabla f(x)\).
This is the mathematical way of saying: the gradient points in the direction of steepest ascent.
Steepest Descent in Practice
Since the gradient tells us where the function increases fastest, it follows that:
- \(\nabla f(x)\) points uphill
- \(-\nabla f(x)\) points downhill
In gradient descent, we take steps like:
\[x^{(t+1)} = x^{(t)} - \eta \nabla f(x^{(t)})\]We’re not just picking any downhill path—we’re taking the steepest descent, the fastest way down the slope at each step.
This behavior becomes clearer when visualized.
Visualization: Directional Derivatives and Descent Arrows
We’ll visualize a few arrows at a point, each representing the directional derivative in a particular direction.
import numpy as np
import matplotlib.pyplot as plt
# Define the function and its gradient
def f(x1, x2):
return x1**2 + 4*x2**2
def grad_f(x1, x2):
return np.array([2*x1, 8*x2])
# Create the grid
x1 = np.linspace(-3, 3, 100)
x2 = np.linspace(-3, 3, 100)
X1, X2 = np.meshgrid(x1, x2)
Z = f(X1, X2)
# Base point and gradient
x0 = np.array([1.0, 1.0])
gradient = grad_f(*x0)
# Normalize the gradient for display (only for arrow length—not math)
grad_unit = gradient / np.linalg.norm(gradient)
# Define direction vectors (unit vectors at 45° intervals)
angles = np.linspace(0, 2*np.pi, 8, endpoint=False)
directions = np.array([[np.cos(a), np.sin(a)] for a in angles])
dot_products = directions @ gradient
# Scale down direction vectors for visualization
arrow_scale = 0.75
scaled_directions = directions * arrow_scale
# Plot
fig, ax = plt.subplots(figsize=(7, 7))
contours = ax.contour(X1, X2, Z, levels=20, cmap='viridis')
ax.clabel(contours, inline=True, fontsize=8)
# Gradient arrow (red)
ax.quiver(*x0, *(grad_unit * arrow_scale * 1.5),
angles='xy', scale_units='xy', scale=1,
color='red', label='Gradient (normalized)', linewidth=2)
# Directional arrows (gray)
for i, vec in enumerate(scaled_directions):
dp = dot_products[i]
ax.quiver(*x0, *vec, angles='xy', scale_units='xy', scale=1,
color='gray', alpha=0.6, linestyle='--')
# Annotations
ax.plot(*x0, 'ko') # Base point
ax.text(x0[0]+0.1, x0[1]+0.1, 'x₀ = (1,1)', fontsize=10)
# Aesthetics
ax.set_xlim(-2.5, 2.5)
ax.set_ylim(-2.5, 2.5)
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_title('Directional Derivatives and Gradient at $x_0 = (1,1)$')
ax.grid(True)
ax.legend()
ax.set_aspect('equal')
plt.tight_layout()
plt.show()
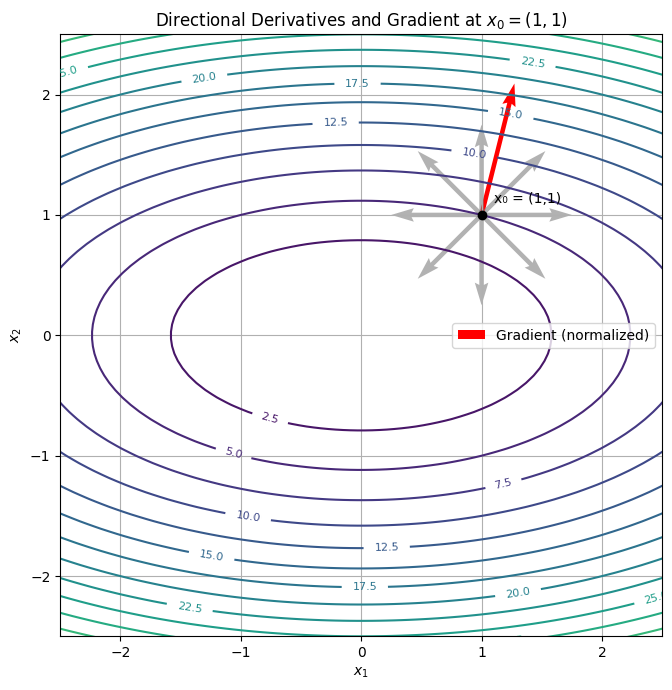
Each gray arrow here represents a possible direction. The longer the arrow, the faster the function increases in that direction. The red arrow is the gradient—always the longest, always the steepest.
Directional derivatives give us a full map of how a function changes in any direction. And when paired with the gradient, they form the compass and topographic lines that guide learning algorithms across loss landscapes.
In the next section, we’ll make this even more concrete: by visualizing level sets—those topographic lines—and seeing how they relate to gradients and optimization paths.
Level Sets and Contour Plots for Loss Surfaces
If you’ve ever hiked with a topographic map, you’ve seen level sets in action. The contour lines on those maps connect points of equal elevation—walk along one, and you won’t go uphill or downhill. In multivariable calculus, we borrow the same idea. A level set of a function is the collection of all points where the function holds a constant value.
For a function \(f(x_1, x_2)\), the level set corresponding to a constant \(c\) is defined as:
\[\{ (x_1, x_2) \in \mathbb{R}^2 \mid f(x_1, x_2) = c \}\]You’ve already seen these in action earlier in this blog—when we plotted the contour lines for our quadratic function. Those closed curves weren’t just for aesthetics. Each one traced out a level set of the function, showing all the places where the loss (or height, or energy) stays the same.
Why Level Sets Matter in Optimization
Level sets give us a kind of “top-down view” of the function. Rather than staring at a 3D surface, we flatten it into slices—like MRI scans of a brain, each layer showing constant intensity. In optimization, this is incredibly helpful:
- We can visualize the shape of the objective function.
- We see whether it’s symmetric, skewed, or steep in some directions.
- And perhaps most importantly: we see how the gradient interacts with the terrain.
One key geometric insight:
The gradient vector at a point is always perpendicular to the level set passing through that point.
This makes sense intuitively: if you’re walking along a path where the function doesn’t change, then the direction in which it does change must be orthogonal to your path. The gradient points that way—cutting across contour lines at 90 degrees.
Let’s revisit the same function from before:
\[f(x_1, x_2) = x_1^2 + 4x_2^2\]Its level sets are ellipses. Why ellipses? Because \(x_1\) and \(x_2\) contribute differently to the value of \(f\)—the \(x_2\) term grows four times as fast, so the contours are “squeezed” along that axis.
Here’s a cleaner contour plot with the gradient field superimposed—now normalized so you can clearly see the relationship.
import numpy as np
import matplotlib.pyplot as plt
# Function and gradient
def f(x1, x2):
return x1**2 + 4*x2**2
def grad_f(x1, x2):
return np.array([2*x1, 8*x2])
# Grid for plotting
x1 = np.linspace(-3, 3, 30)
x2 = np.linspace(-3, 3, 30)
X1, X2 = np.meshgrid(x1, x2)
Z = f(X1, X2)
# Compute gradients
grad_x1 = 2 * X1
grad_x2 = 8 * X2
# Normalize gradients for consistent arrow size
norm = np.sqrt(grad_x1**2 + grad_x2**2)
grad_x1_norm = grad_x1 / norm
grad_x2_norm = grad_x2 / norm
# Plot
fig, ax = plt.subplots(figsize=(8, 6))
contours = ax.contour(X1, X2, Z, levels=20, cmap='viridis')
ax.clabel(contours, inline=True, fontsize=8)
# Quiver (gradient field)
ax.quiver(X1, X2, grad_x1_norm, grad_x2_norm, color='red', alpha=0.7)
# Annotations
ax.set_title('Level Sets and Gradient Field of $f(x_1, x_2) = x_1^2 + 4x_2^2$')
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.grid(True)
ax.set_aspect('equal')
plt.tight_layout()
plt.show()

- Each contour line corresponds to a constant value of the function. Think of them as elevation rings.
- The red arrows represent gradient directions—always pointing perpendicular to the contour lines.
- Where the lines are dense (along the \(x_2\) axis), the slope is steep; where they’re sparse, it’s flatter.
This is more than geometry—it’s optimization logic. In gradient descent, your updates slice across level sets, driving the parameters downhill. The shape of these contours can tell you whether your optimizer might struggle: narrow valleys, plateaus, saddle points—they all show up in this view.
Jacobian Matrix: Shape, Interpretation, and When It Matters
Until now, we’ve focused on scalar-valued functions—those that take a vector and return a number. Loss functions, for instance, are like that: they take in weights or inputs and return a single value to minimize.
But many functions we work with in machine learning go a step further. They take a vector and return another vector.
Think about:
- The output of a neural network layer
- The softmax function over logits
- A transformation from an input image to an embedding vector
These are vector-valued functions, written generally as:
\[\mathbf{f} : \mathbb{R}^n \rightarrow \mathbb{R}^m\]So how do we talk about “how the function changes” now? There’s no longer just one slope to follow—there are multiple outputs, each changing with multiple inputs.
That’s where the Jacobian matrix comes in.
What Is the Jacobian?
Suppose we have a function:
\[\mathbf{f}(x) = \begin{bmatrix} f_1(x_1, \dots, x_n) \\ f_2(x_1, \dots, x_n) \\ \vdots \\ f_m(x_1, \dots, x_n) \end{bmatrix}\]The Jacobian matrix collects all the partial derivatives into an \(m \times n\) matrix:
\[J_{\mathbf{f}}(x) = \begin{bmatrix} \frac{\partial f_1}{\partial x_1} & \cdots & \frac{\partial f_1}{\partial x_n} \\ \frac{\partial f_2}{\partial x_1} & \cdots & \frac{\partial f_2}{\partial x_n} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_m}{\partial x_1} & \cdots & \frac{\partial f_m}{\partial x_n} \end{bmatrix}\]Each row corresponds to the gradient of a single output component. Each column tells us how a particular input influences all the outputs.
A Concrete Example
Let’s say:
\[\mathbf{f}(x_1, x_2) = \begin{bmatrix} x_1^2 + x_2 \\ \sin(x_1) + x_1 x_2 \end{bmatrix}\]Then the Jacobian is:
\[J_{\mathbf{f}}(x_1, x_2) = \begin{bmatrix} 2x_1 & 1 \\ \cos(x_1) + x_2 & x_1 \end{bmatrix}\]At \((x_1, x_2) = (1, 2)\):
\[J_{\mathbf{f}}(1, 2) \approx \begin{bmatrix} 2 & 1 \\ 2.54 & 1 \end{bmatrix}\](using \(\cos(1) \approx 0.54\))
This matrix tells us exactly how changes in \(x_1\) and \(x_2\) influence both components of \(\mathbf{f}\) at that point.
Geometric Interpretation — What the Jacobian Really Does
Let’s pause here—and really sit with this. Because this is where the Jacobian turns from a matrix of partial derivatives into something you can see and feel.
Imagine you’re standing at a point in \(\mathbb{R}^2\)—say, a point in the input space of a neural network layer. Now imagine nudging that point slightly—maybe one unit step in the \(x_1\) direction, or maybe a diagonal step that mixes \(x_1\) and \(x_2\).
What happens to the output?
That’s the question the Jacobian answers.
Think of the Jacobian as a Local Transformer
If \(\mathbf{f} : \mathbb{R}^n \rightarrow \mathbb{R}^m\) is differentiable, then around any point \(\mathbf{x}_0\), it behaves almost like a linear map:
\[\mathbf{f}(\mathbf{x}_0 + \Delta \mathbf{x}) \approx \mathbf{f}(\mathbf{x}_0) + J_{\mathbf{f}}(\mathbf{x}_0) \cdot \Delta \mathbf{x}\]So, locally, the function is its Jacobian. Tiny input changes get multiplied by the Jacobian to yield tiny output changes.
Visual Intuition in 2D
Back to our earlier example:
\[\mathbf{f}(x_1, x_2) = \begin{bmatrix} x_1^2 + x_2 \\ \sin(x_1) + x_1 x_2 \end{bmatrix}\]At \(x = (1, 2)\), we can ask:
- What happens if I take a small step in the \(x_1\) direction?
- What happens if I take a small step in the \(x_2\) direction?
The Jacobian tells us: here’s the resulting direction and magnitude in output space. And those output vectors become the columns of the Jacobian. That’s why the Jacobian captures not just the rate of change, but the entire directional behavior.
A Local Linear Map
You can think of the Jacobian as defining a new local basis in output space.
- A square in input space becomes a parallelogram in output space.
- A circle might get sheared or stretched.
If the Jacobian is diagonal with large entries → it stretches.
If it’s singular → it squashes input into a lower dimension.
If it includes off-diagonal terms → it twists and shears.
Visualizing the Transformation
import numpy as np
import matplotlib.pyplot as plt
# Define the function
def f(x1, x2):
f1 = x1**2 + x2
f2 = np.sin(x1) + x1 * x2
return np.array([f1, f2])
# Define Jacobian
def jacobian(x1, x2):
df1_dx1 = 2 * x1
df1_dx2 = 1
df2_dx1 = np.cos(x1) + x2
df2_dx2 = x1
return np.array([
[df1_dx1, df1_dx2],
[df2_dx1, df2_dx2]
])
# Evaluate at point
x0 = np.array([1.0, 2.0])
J = jacobian(*x0)
# Unit vectors in input space
unit_x = np.array([1, 0])
unit_y = np.array([0, 1])
# Map through Jacobian
mapped_x = J @ unit_x
mapped_y = J @ unit_y
# Plot
fig, ax = plt.subplots(figsize=(7, 6))
# Original unit vectors (input space)
ax.quiver(0, 0, 1, 0, angles='xy', scale_units='xy', scale=1, color='blue', label='Input: $x_1$')
ax.quiver(0, 0, 0, 1, angles='xy', scale_units='xy', scale=1, color='green', label='Input: $x_2$')
# Jacobian-transformed vectors (output space)
ax.quiver(0, 0, mapped_x[0], mapped_x[1], angles='xy', scale_units='xy', scale=1,
color='blue', alpha=0.5, label='Output: $J \\cdot x_1$')
ax.quiver(0, 0, mapped_y[0], mapped_y[1], angles='xy', scale_units='xy', scale=1,
color='green', alpha=0.5, label='Output: $J \\cdot x_2$')
# Plot settings
ax.set_xlim(-1, 3)
ax.set_ylim(-1, 4)
ax.set_aspect('equal')
ax.set_xlabel('Output $f_1$')
ax.set_ylabel('Output $f_2$')
ax.set_title('Jacobian as a Local Linear Map')
ax.grid(True)
ax.legend()
plt.tight_layout()
plt.show()
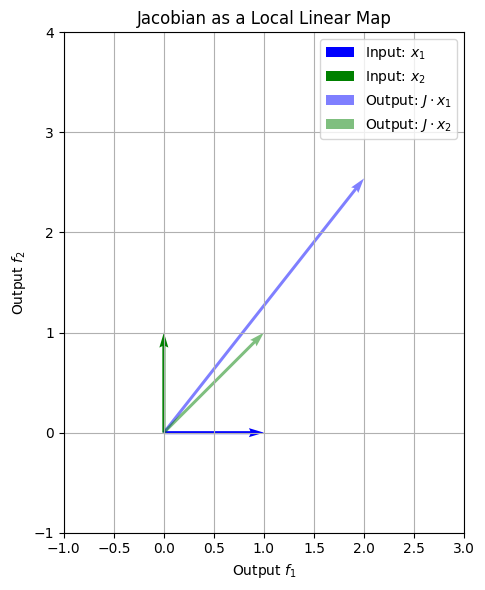
This plot shows how small, axis-aligned steps in input space transform into new vectors in output space. The directions and magnitudes of these arrows encode the local geometry of \(\mathbf{f}\) at that point.
Where the Jacobian Matters in ML
- In backpropagation, each layer’s transformation is tracked via Jacobians. Gradients pass backward by chaining Jacobians via the multivariable chain rule.
- In normalizing flows, the Jacobian determinant tracks how volume changes during transformation—a core step in computing likelihoods.
- In coordinate transformations, it accounts for how measures like length, area, or probability density distort under nonlinear mappings.
So to sum it up:
The Jacobian is the best linear approximation to a function at a point. It doesn’t just say how fast something changes—it tells you in what direction, how much, and with what distortion. It’s the local shape of the function—captured in a matrix.
When linear isn’t enough—when curvature, twists, and second-order behavior begin to matter—we need something more powerful.
Let’s now explore the Hessian matrix, and see how the landscape bends.
Hessian Matrix: Curvature, Convexity, and Second-Order Conditions
The gradient tells us how steeply a function rises or falls in different directions. But that’s only part of the story. It tells you the slope—but not how the slope is changing.
What if the function curves gently in one direction but sharply in another? What if the slope is zero, but you’re at a saddle point, not a minimum?
To answer these questions, we need second derivatives. And in multivariable calculus, they come packed into a matrix: the Hessian.
What Is the Hessian?
Let’s start with a scalar-valued function:
\[f: \mathbb{R}^n \rightarrow \mathbb{R}\]The Hessian matrix of \(f\) at a point \(x\) is the matrix of all second-order partial derivatives:
\[H_f(x) = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_1 \partial x_n} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} & \cdots & \frac{\partial^2 f}{\partial x_2 \partial x_n} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^2 f}{\partial x_n \partial x_1} & \frac{\partial^2 f}{\partial x_n \partial x_2} & \cdots & \frac{\partial^2 f}{\partial x_n^2} \end{bmatrix}\]Each entry in the matrix tells you how one slope is changing with respect to another variable.
In short:
- Diagonal entries → curvature along coordinate axes
- Off-diagonal entries → interaction between variables (e.g., how \(x_1\) affects the rate of change along \(x_2\))
What About Vector-Valued Functions?
So far, we’ve assumed that our function maps from \(\mathbb{R}^n\) to \(\mathbb{R}\)—a single output. But in many machine learning settings, especially in neural nets and transformation models, our functions are vector-valued:
\[\mathbf{f} : \mathbb{R}^n \rightarrow \mathbb{R}^m\]When \(m = 1\), we can use the Hessian directly.
But when \(m > 1\), things get more complex. There’s no single Hessian matrix—instead, each output dimension can have its own Hessian.
So the second-order derivative of a vector-valued function becomes a rank-3 tensor:
- For each output component \(f_i\), you can compute a Hessian:
\(H_{f_i} \in \mathbb{R}^{n \times n}\) -
The full second-order derivative of \(\mathbf{f}\) is then a stack of \(m\) Hessian matrices:
\[\frac{\partial^2 \mathbf{f}}{\partial \mathbf{x}^2} \in \mathbb{R}^{m \times n \times n}\]
This shows up in advanced applications like:
- Second-order backpropagation
- Differential geometry
- Optimization with vector-valued objectives (e.g., multi-task learning)
But in most ML workflows, we apply the Hessian primarily to scalar loss functions—even when they come from a vector-valued prediction model.
Example: A Classic Quadratic Bowl
Let’s return to a familiar surface:
\[f(x_1, x_2) = x_1^2 + 4x_2^2\]Compute the partials:
- \(\frac{\partial f}{\partial x_1} = 2x_1\), \(\frac{\partial^2 f}{\partial x_1^2} = 2\)
- \(\frac{\partial f}{\partial x_2} = 8x_2\), \(\frac{\partial^2 f}{\partial x_2^2} = 8\)
- Mixed partials: \(\frac{\partial^2 f}{\partial x_1 \partial x_2} = 0\)
So the Hessian is:
\[H_f(x) = \begin{bmatrix} 2 & 0 \\ 0 & 8 \end{bmatrix}\]This tells us something immediately about the shape of the function: it curves more steeply along the \(x_2\) direction than along \(x_1\).
What It Means for a Function to “Curve More Steeply”
Let’s unpack that visually and intuitively.
The second derivative with respect to \(x_1\) is 2, and with respect to \(x_2\) is 8. That means:
If you walk in the \(x_1\) direction, the slope increases gradually.
But if you walk in the \(x_2\) direction, the slope rises much faster.
The function is bending upward four times faster along \(x_2\).
And that matches what we saw earlier in the contour plots:
- The level curves are ellipses, stretched wide along \(x_1\), squished along \(x_2\).
- Contour lines are farther apart where the function grows slowly, and closer together where the surface bends sharply.
- So the Hessian, through its entries, is encoding the very curvature we visualized before.
Interpreting the Hessian
1. Curvature
The Hessian tells you the local curvature of the function. If you think of \(f\) as a landscape, the Hessian tells you if you’re standing on a peak, a pit, a ridge, or a saddle.
2. Convexity
The Hessian also tells you whether the function is convex or not.
- If \(H_f(x)\) is positive definite (all eigenvalues > 0), the function is strictly convex.
- If it’s indefinite (some eigenvalues negative), you’re in a saddle region.
- If it’s negative definite, you’re sitting on a hilltop.
So convex optimization boils down to checking the eigenvalues of the Hessian.
Geometric Visualization: Contours + Curvature
Let’s revisit the same quadratic surface, now with the Hessian’s influence embedded in the shape.
import numpy as np
import matplotlib.pyplot as plt
# Quadratic function and constant Hessian
def f(x1, x2):
return x1**2 + 4*x2**2
def hessian():
return np.array([[2, 0], [0, 8]])
# Grid for contour plot
x1 = np.linspace(-2.5, 2.5, 400)
x2 = np.linspace(-2.5, 2.5, 400)
X1, X2 = np.meshgrid(x1, x2)
Z = f(X1, X2)
# Compute Hessian eigendecomposition
H = hessian()
eigvals, eigvecs = np.linalg.eig(H)
# Set up plot
fig, ax = plt.subplots(figsize=(7, 7))
contours = ax.contour(X1, X2, Z, levels=40, cmap='viridis')
ax.clabel(contours, inline=True, fontsize=8)
# Curvature vectors from eigenvectors
origin = np.array([0, 0])
colors = ['crimson', 'darkorange']
labels = [f'Curvature dir 1 ($\\lambda$={eigvals[0]:.0f})',
f'Curvature dir 2 ($\\lambda$={eigvals[1]:.0f})']
display_length = 2.2
for i in range(2):
direction = eigvecs[:, i] / np.linalg.norm(eigvecs[:, i])
vec = direction * display_length
ax.quiver(*origin, vec[0], vec[1],
angles='xy', scale_units='xy', scale=1,
color=colors[i], width=0.017,
headwidth=8, headlength=10,
label=labels[i])
# Add boxed text for annotation labels
ax.text(2.3, -0.2, 'Gentler curvature',
color='black', fontsize=10, va='center',
bbox=dict(facecolor='white', edgecolor='black', boxstyle='round,pad=0.2'))
ax.text(0.4, 1.6, 'Steeper curvature',
color='black', fontsize=10, va='center', rotation=90,
bbox=dict(facecolor='white', edgecolor='black', boxstyle='round,pad=0.2'))
# Final plot aesthetics
ax.set_title('Contours and Principal Curvature Directions of $f(x_1, x_2) = x_1^2 + 4x_2^2$')
ax.set_xlabel('$x_1$')
ax.set_ylabel('$x_2$')
ax.set_xlim(-2.5, 2.5)
ax.set_ylim(-2.5, 2.5)
ax.grid(True)
ax.set_aspect('equal')
ax.legend()
plt.tight_layout()
plt.show()
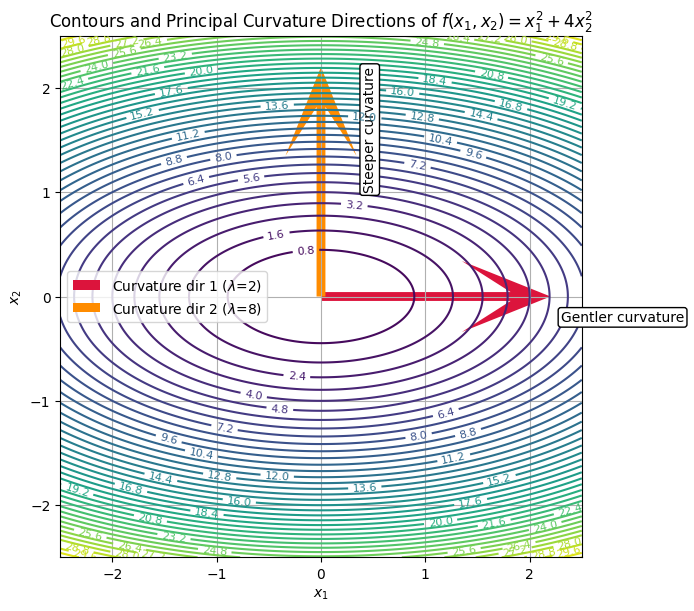
This plot shows how the Hessian’s eigenvectors correspond to the principal curvature directions—and their eigenvalues tell us how steeply the function bends in each of those directions.
Why the Hessian Matters in Machine Learning
- Newton’s method: Optimization algorithms like Newton’s method use the Hessian to take curvature-aware steps.
- Second-order optimization: When the gradient alone isn’t enough, the Hessian can help escape saddle points or accelerate convergence.
- Uncertainty estimation: In Bayesian learning, the inverse of the Hessian approximates the posterior variance near a maximum likelihood solution.
- Vector-valued systems: Even though we typically apply Hessians to scalar losses, many of those losses come from vector-valued models—so understanding when and how to generalize second-order derivatives matters in deep learning and differential programming.
Classifying Critical Points Using the Hessian
Earlier, we learned that critical points occur where the gradient of a function vanishes:
\[\nabla f(x) = 0\]But just finding critical points is not enough.
A critical point could be:
- a local minimum (lowest nearby point),
- a local maximum (highest nearby point),
- or a saddle point (neither minimum nor maximum; curves up in some directions and down in others).
Question:
How do we tell what kind of critical point it is?
This is where the Hessian matrix comes in.
The Hessian generalizes the idea of a “second derivative” from single-variable calculus to multiple dimensions.
Step-by-Step Example
Let’s work through the simple function:
\[f(x, y) = x^2 + y^2\]First, compute first-order derivatives (gradient):
\[\nabla f(x, y) = \begin{bmatrix} \frac{\partial f}{\partial x} \\ \frac{\partial f}{\partial y} \end{bmatrix} = \begin{bmatrix} 2x \\ 2y \end{bmatrix}\]Setting the gradient to zero:
\[\nabla f(x, y) = 0 \quad \Rightarrow \quad 2x = 0,\quad 2y = 0\]gives the critical point:
\[(x, y) = (0, 0)\]Now, compute second-order derivatives for the Hessian:
- \[\frac{\partial^2 f}{\partial x^2} = 2\]
- \[\frac{\partial^2 f}{\partial y^2} = 2\]
- \[\frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x} = 0\]
Thus, the Hessian matrix is:
\[H_f(x, y) = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}\]This matrix is constant (independent of \(x\) and \(y\)), because the function is a simple quadratic.
What Does the Hessian Tell Us?
The key is to analyze the eigenvalues of the Hessian:
- If all eigenvalues are positive, \(H\) is positive definite ➔ local minimum.
- If all eigenvalues are negative, \(H\) is negative definite ➔ local maximum.
- If eigenvalues have mixed signs, \(H\) is indefinite ➔ saddle point.
In our example:
- The eigenvalues of \(\begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}\) are just 2 and 2 (both positive).
So, the critical point at \((0, 0)\) is a local minimum.
Specifically:
| Condition | Meaning | Surface Behavior |
|---|---|---|
| All eigenvalues positive | Positive definite | Curves upward in every direction — local minimum |
| All eigenvalues negative | Negative definite | Curves downward in every direction — local maximum |
| Mixed signs (some positive, some negative) | Indefinite | Curves up in some directions, down in others — saddle point |
Intuitive Picture
Think about standing at a point on a mountain:
- If in every direction around you the ground slopes upward (like standing in a valley), you’re at a local minimum.
- If in every direction the ground slopes downward (like standing at a mountain peak), you’re at a local maximum.
- If the ground slopes up in some directions and down in others (like standing on a mountain pass or a saddle), you’re at a saddle point.
The Hessian captures exactly this multi-directional curvature information through its eigenvalues.
Mathematical Viewpoint
Suppose you take a small step \(\Delta x\) from the critical point.
Using a Taylor approximation:
\[f(x + \Delta x) \approx f(x) + \frac{1}{2} \Delta x^T H \Delta x\]- If \(H\) is positive definite (all eigenvalues > 0), then \(\Delta x^T H \Delta x > 0\) for every \(\Delta x \neq 0\).
- This means \(f(x+\Delta x) > f(x)\), so you’re at a local minimum.
- If \(H\) is negative definite (all eigenvalues < 0), then \(\Delta x^T H \Delta x < 0\) for every \(\Delta x \neq 0\).
- This means \(f(x+\Delta x) < f(x)\), so you’re at a local maximum.
- If \(H\) has mixed eigenvalues, depending on the direction you step, \(\Delta x^T H \Delta x\) can be positive (uphill) or negative (downhill).
- This is the saddle point situation.
A General Quick Test for 2D Functions
For a \(2 \times 2\) Hessian:
\[H = \begin{bmatrix} a & b \\ b & c \end{bmatrix}\]you can also classify using determinants:
- If \(\det(H) > 0\) and \(a > 0\) ➔ local minimum.
- If \(\det(H) > 0\) and \(a < 0\) ➔ local maximum.
- If \(\det(H) < 0\) ➔ saddle point.
(Here, \(\det(H) = ac - b^2\).)
In our case:
\(\det(H) = (2)(2) - (0)^2 = 4 > 0\) and \(a = 2 > 0\)
Again confirming local minimum.
Why It Matters in Machine Learning
When optimizing a loss function, it’s not enough to reach a critical point.
You want to know whether it’s actually useful:
- Minima are where learning converges (good).
- Saddle points can trap optimization algorithms, causing slow learning.
- Maxima are typically unstable for loss functions (rarely desirable).
In deep learning especially, loss surfaces are filled with saddle points.
Advanced optimizers (like SGD with momentum, Adam) are partly designed to escape saddle points rather than getting stuck.
Being able to classify critical points helps you understand why optimization behaves the way it does—and why sometimes, even reaching a gradient near zero isn’t the end of the story.
Applications
Perfect. Now that we’ve built strong geometric and mathematical intuition for gradients, directional derivatives, level sets, Jacobians, and Hessians, it’s time to put that machinery to work in the kinds of problems data scientists and ML engineers actually face.
Let’s now transition into real-world applications of these concepts—starting with the behavior of gradients on loss landscapes.
Interpreting Gradients in Loss Landscapes
In machine learning, the loss function plays the role of the landscape. Each point in parameter space corresponds to a particular set of model weights, and the loss tells us how well those weights perform.
And just like in our geometric visualizations earlier, the gradient tells us which way to move in that space to reduce error.
But here’s the twist: unlike a clean quadratic bowl, real-world loss surfaces aren’t always smooth, convex, or well-behaved.
They’re messy. They have flat regions, sharp cliffs, narrow ravines, and saddle points.
And gradients are our only compass.
What Does a Loss Landscape Look Like?
Let’s imagine a basic example: linear regression with two parameters.
We can visualize the mean squared error (MSE) loss surface for this model:
\[\hat{y} = w_1 x_1 + w_2 x_2 \\ \mathcal{L}(w_1, w_2) = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2\]The function \(\mathcal{L}(w_1, w_2)\) is quadratic and convex. That means:
- The loss surface is shaped like a bowl
- The gradient at any point points directly toward the minimum
- The contours are ellipses, centered at the best-fit weights
Let’s build a synthetic dataset and visualize what the gradient field looks like.
Visualization: Gradient Field on a Loss Surface
import numpy as np
import matplotlib.pyplot as plt
# Generate synthetic data
np.random.seed(0)
X = np.random.randn(100, 2)
true_w = np.array([2.0, -3.0])
y = X @ true_w + np.random.randn(100) * 0.5
# Loss function (MSE)
def loss(w):
y_pred = X @ w
return np.mean((y - y_pred) ** 2)
# Gradient of loss
def grad(w):
y_pred = X @ w
return -2 * X.T @ (y - y_pred) / len(y)
# Create a grid over weight space
w1_vals = np.linspace(-4, 5, 40)
w2_vals = np.linspace(-6, 3, 40)
W1, W2 = np.meshgrid(w1_vals, w2_vals)
Z = np.array([[loss(np.array([w1, w2])) for w1, w2 in zip(row1, row2)]
for row1, row2 in zip(W1, W2)])
# Gradient vectors at each grid point
Gx = np.zeros_like(W1)
Gy = np.zeros_like(W2)
for i in range(W1.shape[0]):
for j in range(W1.shape[1]):
w = np.array([W1[i, j], W2[i, j]])
g = grad(w)
Gx[i, j], Gy[i, j] = -g # Negative gradient (descent direction)
# Normalize gradients for display
norm = np.sqrt(Gx**2 + Gy**2)
Gx /= norm + 1e-8
Gy /= norm + 1e-8
# Plot
fig, ax = plt.subplots(figsize=(8, 6))
contours = ax.contour(W1, W2, Z, levels=30, cmap='viridis')
ax.clabel(contours, inline=True, fontsize=8)
ax.quiver(W1, W2, Gx, Gy, color='red', alpha=0.7, width=0.003)
# Mark the true minimum
ax.plot(true_w[0], true_w[1], 'ko', label='True minimum')
# Aesthetics
ax.set_title('Gradient Field on Loss Surface (Linear Regression)')
ax.set_xlabel('$w_1$')
ax.set_ylabel('$w_2$')
ax.legend()
ax.grid(True)
plt.tight_layout()
plt.show()
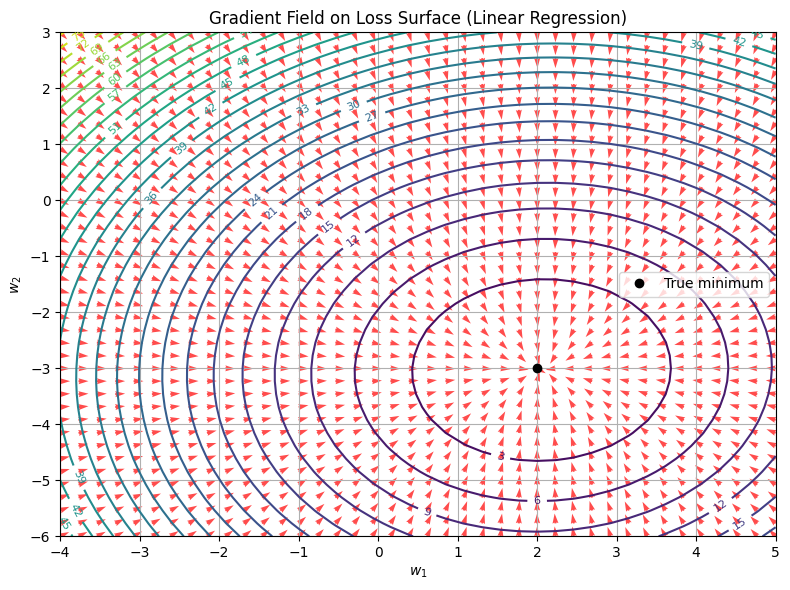
- The red arrows show the gradient descent direction at each point.
- All arrows point inward, toward the global minimum—the best-fit weights.
- Contours are elliptical, reflecting the quadratic structure of MSE.
- The gradient magnitudes are stronger further out, and shrink as we approach the minimum—matching our earlier theory of gradient flow.
This is the ideal case: smooth, convex, easy to optimize. But real-world models, like deep neural networks, rarely give you this luxury.
Beyond Quadratics: When Gradients Struggle
In high-dimensional models:
- Gradients might vanish (flat regions)
- Or explode (near cliffs or chaotic boundaries)
- Or zigzag due to curvature imbalance (like a narrow ravine)
The surface might be non-convex, filled with:
- Multiple local minima
- Saddle points
- Flat valleys and deceptive ridges
In these cases, understanding gradients—and their limitations—becomes even more important. And that’s where second-order information like the Hessian can help.
But even in simpler models like logistic regression, you’ll see how gradients steer learning in powerful ways.
Visualizing Cost Functions for Logistic Regression
Great—let’s now look at how these geometric and differential ideas show up in another foundational ML model: logistic regression.
While the linear regression loss surface was a perfect bowl, logistic regression introduces a non-linearity via the sigmoid, which slightly warps the loss surface—but still keeps it convex. This makes it a beautiful example for understanding gradient flow and cost geometry beyond quadratics.
In logistic regression, we’re not predicting continuous values—we’re predicting probabilities. Specifically, we model:
\[\hat{y} = \sigma(w^T x) = \frac{1}{1 + e^{-w^T x}}\]Then we compare \(\hat{y}\) with the actual labels \(y \in \{0, 1\}\) using the binary cross-entropy (log loss):
\[\mathcal{L}(w) = -\frac{1}{n} \sum_{i=1}^n \left[ y_i \log \hat{y}_i + (1 - y_i) \log (1 - \hat{y}_i) \right]\]This function is still convex, but not quadratic. Its surface is warped—flatter in some areas, steeper in others—and has no closed-form minimum like MSE. But gradients still point us toward the best weights.
Let’s Visualize the Cost Surface
We’ll create a simple 2D dataset with binary labels, train a logistic regression model, and plot how the loss surface behaves as we vary \(w_1\) and \(w_2\).
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import expit as sigmoid
# Create toy classification dataset
np.random.seed(42)
X = np.random.randn(100, 2)
true_w = np.array([2.0, -3.0])
logits = X @ true_w
y = (sigmoid(logits) > 0.5).astype(int)
# Logistic loss function
def loss(w):
logits = X @ w
preds = sigmoid(logits)
eps = 1e-10 # numerical stability
return -np.mean(y * np.log(preds + eps) + (1 - y) * np.log(1 - preds + eps))
# Grid over weight space
w1_vals = np.linspace(-4, 5, 100)
w2_vals = np.linspace(-6, 4, 100)
W1, W2 = np.meshgrid(w1_vals, w2_vals)
Z = np.array([[loss(np.array([w1, w2])) for w1, w2 in zip(row1, row2)]
for row1, row2 in zip(W1, W2)])
# Plot the loss surface
fig, ax = plt.subplots(figsize=(8, 6))
contours = ax.contour(W1, W2, Z, levels=40, cmap='plasma')
ax.clabel(contours, inline=True, fontsize=8)
# Mark the true weights
ax.plot(true_w[0], true_w[1], 'ko', label='True weights')
# Aesthetics
ax.set_title('Logistic Regression Loss Surface')
ax.set_xlabel('$w_1$')
ax.set_ylabel('$w_2$')
ax.grid(True)
ax.legend()
plt.tight_layout()
plt.show()
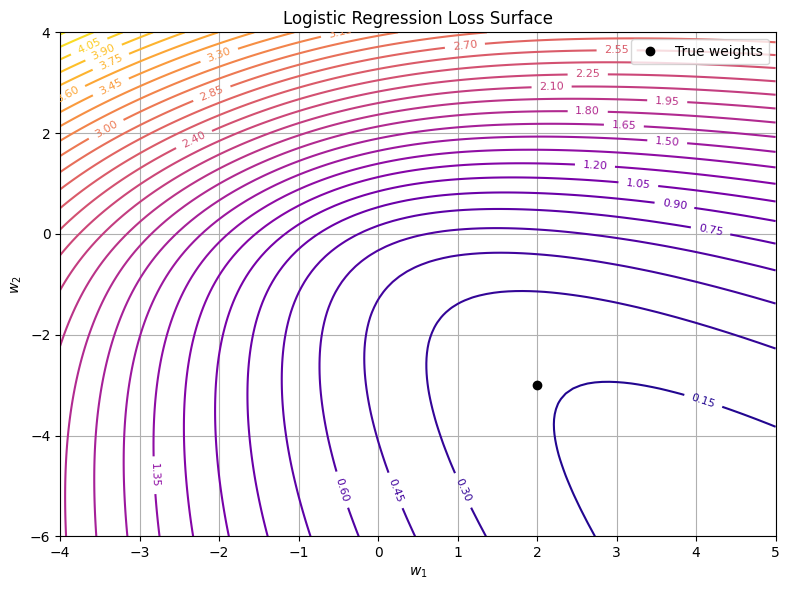
- The surface is not symmetric—it curves differently along \(w_1\) and \(w_2\).
- Still, it’s convex—there’s only one global minimum.
- As you move toward the true weights, the loss consistently decreases.
- Some regions are flatter—meaning smaller gradients, slower learning.
- Others are steeper—meaning faster change and more dramatic updates.
Even without a closed-form solution, gradient descent works well here, precisely because of that convex shape. The gradient always points in a helpful direction—even if you don’t know where the minimum is.
Comparing to Linear Regression
| Feature | Linear Regression | Logistic Regression |
|---|---|---|
| Loss Shape | Perfect bowl (quadratic) | Warped bowl (log-convex) |
| Minimum | Closed-form solution | Requires numerical optimization |
| Contour Shape | Elliptical, symmetric | Elliptical-ish, stretched or tilted |
| Gradient Behavior | Constant rate of change | Varying rates; flatter near optimum |
| Optimization Path | Direct and steady | More sensitive to step size |
This sets us up beautifully for more complex models where the surface is not even convex, and gradients can point in unhelpful directions. But before jumping to deep nets, we can build intuition for how gradients behave across layers, which leads us naturally to…
Layer-Wise Gradients in Neural Networks
In neural networks, we often hear about backpropagation—the algorithm that trains deep models by “flowing gradients backward.” But what does that actually mean, mathematically?
To understand this, we need to return to two ideas we’ve already built up:
- The Jacobian, which tells us how vector-valued functions transform space.
- The chain rule, which helps us understand how derivatives compose through nested functions.
Backpropagation is simply the systematic application of the chain rule across layers—a beautifully recursive structure of Jacobians and gradients.
The Setup
Let’s say we have a simple feedforward neural network:
\[\mathbf{x} \xrightarrow{\;W^{(1)}\;} \mathbf{z}^{(1)} \xrightarrow{\;\phi\;} \mathbf{a}^{(1)} \xrightarrow{\;W^{(2)}\;} \mathbf{z}^{(2)} \xrightarrow{\;\phi\;} \dots \xrightarrow{\text{final layer}} \hat{y}\]Each layer applies:
- A linear transformation: \(\mathbf{z}^{(l)} = W^{(l)} \mathbf{a}^{(l-1)} + \mathbf{b}^{(l)}\)
- A nonlinear activation: \(\mathbf{a}^{(l)} = \phi(\mathbf{z}^{(l)})\)
We want to compute the gradient of the loss with respect to each layer’s parameters: \(\frac{\partial \mathcal{L}}{\partial W^{(l)}}\).
To do this, we propagate the gradient of the loss backward—from output to input.
Backprop: Layer-by-Layer
At the heart of backpropagation is this rule:
\[\frac{\partial \mathcal{L}}{\partial W^{(l)}} = \delta^{(l)} \cdot \left(\mathbf{a}^{(l-1)}\right)^T\]Where:
- \(\delta^{(l)} = \frac{\partial \mathcal{L}}{\partial \mathbf{z}^{(l)}}\) is the error signal at layer \(l\)
- \(\mathbf{a}^{(l-1)}\) is the activation from the previous layer
This gradient is a matrix. The outer product structure arises because we’re taking derivatives of a scalar loss with respect to a matrix of weights.
The recursion for the error signal is:
\[\delta^{(l)} = \left(W^{(l+1)}\right)^T \delta^{(l+1)} \odot \phi'(\mathbf{z}^{(l)})\]This is the multivariable chain rule in action—composed through Jacobians.
Geometric Interpretation
Each layer applies a function:
\[\mathbf{a}^{(l)} = f^{(l)}(\mathbf{a}^{(l-1)})\]So the gradient of the loss w.r.t. earlier layers is:
\[\frac{\partial \mathcal{L}}{\partial \mathbf{a}^{(l-1)}} = J_{f^{(l)}}^T \cdot \frac{\partial \mathcal{L}}{\partial \mathbf{a}^{(l)}}\]That is, we multiply the incoming gradient by the transpose of the Jacobian of the layer.
Layer-by-layer, the gradients are shaped by:
- The activations (\(\mathbf{a}\))
- The Jacobians of each transformation
- The structure of the loss at the end
Table: What Flows Through the Network?
| Quantity | Forward Pass | Backward Pass |
|---|---|---|
| Input | $$\mathbf{x}$$ | – |
| Linear transform | $$\mathbf{z}^{(l)} = W^{(l)} \mathbf{a}^{(l-1)}$$ | Multiply by $$\left(W^{(l)}\right)^T$$ |
| Nonlinearity | $$\mathbf{a}^{(l)} = \phi(\mathbf{z}^{(l)})$$ | Elementwise multiply by $$\phi'(\mathbf{z}^{(l)})$$ |
| Loss | $$\hat{y}, \mathcal{L}(\hat{y}, y)$$ | Start from $$\frac{\partial \mathcal{L}}{\partial \hat{y}}$$ and chain backward |
A Numerical Demo of Backpropagation
Let’s walk through a numerical example using a tiny 1-hidden-layer neural network with ReLU activation and one output neuron.
Problem Setup:
- Input: \(\mathbf{x} = [1, 2]\)
- Hidden layer: 2 neurons, ReLU
- Output: 1 neuron, linear
- True label: \(y = 10\)
- Loss: Mean Squared Error (MSE)
Network Parameters
- Hidden layer weights:
- Output layer weights:
Step 1: Forward Pass
Input to hidden layer:
\[\mathbf{z}^{[1]} = W^{[1]} \cdot \mathbf{x} + \mathbf{b}^{[1]} = \begin{bmatrix} 1 & -1 \\ 2 & 0 \end{bmatrix} \cdot \begin{bmatrix} 1 \\ 2 \end{bmatrix} = \begin{bmatrix} 1 - 2 \\ 2 + 0 \end{bmatrix} = \begin{bmatrix} -1 \\ 2 \end{bmatrix}\]Apply ReLU:
\[\mathbf{a}^{[1]} = \phi(\mathbf{z}^{[1]}) = \begin{bmatrix} \max(0, -1) \\ \max(0, 2) \end{bmatrix} = \begin{bmatrix} 0 \\ 2 \end{bmatrix}\]Output layer:
\[\hat{y} = W^{[2]} \cdot \mathbf{a}^{[1]} + b^{[2]} = [3, -1] \cdot [0, 2] = -2\]Step 2: Compute Loss
Use MSE:
\[\mathcal{L} = \frac{1}{2} (y - \hat{y})^2 = \frac{1}{2} (10 - (-2))^2 = \frac{1}{2} \cdot 144 = 72\]Step 3: Backpropagation
Step 3.1: Gradient of loss w.r.t. output
\[\frac{\partial \mathcal{L}}{\partial \hat{y}} = \hat{y} - y = -2 - 10 = -12\]Step 3.2: Gradient w.r.t. output layer weights
We use:
\[\frac{\partial \mathcal{L}}{\partial W^{[2]}} = \frac{\partial \mathcal{L}}{\partial \hat{y}} \cdot \frac{\partial \hat{y}}{\partial W^{[2]}} = -12 \cdot \mathbf{a}^{[1]} = -12 \cdot \begin{bmatrix} 0 \\ 2 \end{bmatrix} = \begin{bmatrix} 0 \\ -24 \end{bmatrix}\]So:
\[\frac{\partial \mathcal{L}}{\partial W^{[2]}} = \begin{bmatrix} 0 & -24 \end{bmatrix}\]Step 3.3: Backpropagate to hidden layer (chain rule)
We need:
\[\delta^{[1]} = \frac{\partial \mathcal{L}}{\partial \mathbf{z}^{[1]}} = \left( W^{[2]} \right)^T \cdot \frac{\partial \mathcal{L}}{\partial \hat{y}} \odot \phi'(\mathbf{z}^{[1]})\]- \(\phi'(\mathbf{z}^{[1]}) = [0, 1]\) (since ReLU derivative is 0 for negative inputs, 1 for positive)
- \(W^{[2]} = [3, -1]\) → \(\left(W^{[2]}\right)^T = \begin{bmatrix} 3 \\ -1 \end{bmatrix}\)
So:
\[\delta^{[1]} = \begin{bmatrix} 3 \\ -1 \end{bmatrix} \cdot (-12) \odot \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} -36 \\ 12 \end{bmatrix} \odot \begin{bmatrix} 0 \\ 1 \end{bmatrix} = \begin{bmatrix} 0 \\ 12 \end{bmatrix}\]Step 3.4: Gradient w.r.t. hidden layer weights
Use:
\[\frac{\partial \mathcal{L}}{\partial W^{[1]}} = \delta^{[1]} \cdot (\mathbf{x})^T = \begin{bmatrix} 0 \\ 12 \end{bmatrix} \cdot \begin{bmatrix} 1 & 2 \end{bmatrix} = \begin{bmatrix} 0 & 0 \\ 12 & 24 \end{bmatrix}\]Final Gradients Summary
| Parameter | Gradient |
|---|---|
| $$W^{[2]}$$ | $$[0,\ -24]$$ |
| $$W^{[1]}$$ | $$\begin{bmatrix} 0 & 0 \\ 12 & 24 \end{bmatrix}$$ |
Jacobians in Backpropagation
Great—we’ve just seen how gradients flow backward through neural networks using chain rules and Jacobians. Now let’s step into how Jacobians (and sometimes Hessians) show up inside those gradients, especially when the outputs themselves are vector-valued.
Backpropagation is often taught as a mechanical algorithm: compute forward, cache values, compute gradients backward. But under the hood, what we’re really doing is composing Jacobian matrices of every layer.
The power of this interpretation? It lets you understand:
- Why gradients flow the way they do
- How they’re affected by each transformation
- How automatic differentiation frameworks like PyTorch and TensorFlow actually work
Recap: The Chain Rule, Vector Version
For scalar functions, we’re used to:
\[\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}\]In vector calculus, this becomes:
\[J_{f \circ g}(x) = J_f(g(x)) \cdot J_g(x)\]That is, the Jacobian of a composition is the product of Jacobians.
This is the real backbone of backpropagation.
A Simple Example: 2-Layer Network with Vector Output
Suppose your network looks like this:
\[\mathbf{x} \in \mathbb{R}^2\] \[\mathbf{z}^{[1]} = W^{[1]} \cdot \mathbf{x} \in \mathbb{R}^3\] \[\mathbf{a}^{[1]} = \phi(\mathbf{z}^{[1]}) \in \mathbb{R}^3\] \[\mathbf{z}^{[2]} = W^{[2]} \cdot \mathbf{a}^{[1]} \in \mathbb{R}^2\] \[\hat{\mathbf{y}} = \phi(\mathbf{z}^{[2]}) \in \mathbb{R}^2\]Assume your loss function is:
\[\mathcal{L} = \frac{1}{2} \|\hat{\mathbf{y}} - \mathbf{y}\|^2\]To compute \(\frac{\partial \mathcal{L}}{\partial W^{[1]}}\), we need:
- The Jacobian of the loss with respect to \(\hat{\mathbf{y}}\)
- The Jacobian of \(\hat{\mathbf{y}}\) with respect to \(\mathbf{z}^{[2]}\)
- The Jacobian of \(\mathbf{z}^{[2]}\) with respect to \(\mathbf{a}^{[1]}\)
- The Jacobian of \(\mathbf{a}^{[1]}\) with respect to \(\mathbf{z}^{[1]}\)
- And finally, \(\frac{\partial \mathbf{z}^{[1]}}{\partial W^{[1]}}\)
Matrix Multiplication of Jacobians
Let’s define each transformation and then apply the chain rule with Jacobians.
Step-by-step Jacobian flow:
\[\frac{\partial \mathcal{L}}{\partial W^{[1]}} = \underbrace{\frac{\partial \mathcal{L}}{\partial \hat{\mathbf{y}}}}_{\text{(2x1)}} \cdot \underbrace{J_{\hat{\mathbf{y}} \leftarrow \mathbf{z}^{[2]}}}_{(2x2)} \cdot \underbrace{J_{\mathbf{z}^{[2]} \leftarrow \mathbf{a}^{[1]}}}_{(2x3)} \cdot \underbrace{J_{\mathbf{a}^{[1]} \leftarrow \mathbf{z}^{[1]}}}_{(3x3)} \cdot \underbrace{\frac{\partial \mathbf{z}^{[1]}}{\partial W^{[1]}}}_{(3x2x2)}\]Technically, the last term is a tensor—because we’re differentiating a matrix output w.r.t. a matrix input. But you can also think of it row-by-row.
Each Jacobian tells you: how does output move if I wiggle the previous layer? And backprop is just: multiply those movements step by step, using the transpose of the Jacobians.
How Autograd Libraries Do It
Autograd engines like PyTorch and TensorFlow build a computation graph behind the scenes. Each node:
- Stores its forward value
- Stores the Jacobian (or more precisely, its pullback rule)
- Chains them backward using reverse-mode differentiation
In PyTorch:
-
.backward()walks through this chain of Jacobians - It avoids computing full Jacobian matrices—just applies Jacobian-vector products (JVPs)
This is much more memory efficient than storing all Jacobians.
Table: Jacobians Through Layers
| Operation | Forward | Jacobian or Gradient |
|---|---|---|
| Loss (MSE) | $$\mathcal{L} = \frac{1}{2} \|\hat{y} - y\|^2$$ | $$\frac{\partial \mathcal{L}}{\partial \hat{y}} = \hat{y} - y$$ |
| Linear | $$\mathbf{z} = W \cdot \mathbf{x}$$ | $$\mathbb{R}^{\text{out} \times \text{in}}$$ |
| ReLU | $$\mathbf{a} = \max(0,\ \mathbf{z})$$ | $$\text{Diagonal} \in \mathbb{R}^{n \times n}$$ |
| Sigmoid | $$\sigma(z) = \frac{1}{1 + e^{-z}}$$ | $$\text{Diagonal: } \sigma(z)(1 - \sigma(z))$$ |
Why This Matters
Seeing backprop through the lens of Jacobians gives you:
- A deeper understanding of how gradient flow works
- The ability to debug and design custom layers
- A way to extend to second-order methods, where Jacobians and Hessians matter
Hessians in Newton’s Method
Gradient descent tells you which way to move to reduce loss. But it doesn’t tell you how far to move with confidence. It assumes a simple landscape and takes cautious steps.
What if the surface isn’t symmetric?
What if it curves more sharply in some directions than others?
That’s exactly what the Hessian matrix captures—and Newton’s method uses it to take curvature-aware steps.
Gradient Descent vs. Newton’s Method
-
Gradient descent updates:
\[\theta_{t+1} = \theta_t - \eta \cdot \nabla \mathcal{L}(\theta_t)\] -
Newton’s method uses:
\[\theta_{t+1} = \theta_t - H^{-1}(\theta_t) \cdot \nabla \mathcal{L}(\theta_t)\]
Here, \(H\) is the Hessian of the loss function, and the inverse adjusts for the local curvature. When the surface is steep in one direction and flat in another, Newton’s method scales the step accordingly—big where it’s flat, small where it’s sharp.
How It Works Geometrically
Let’s say you’re minimizing a scalar function \(f: \mathbb{R}^n \rightarrow \mathbb{R}\). Around any point \(\theta\), you can do a second-order Taylor approximation:
\[f(\theta + \Delta \theta) \approx f(\theta) + \nabla f(\theta)^T \Delta \theta + \frac{1}{2} \Delta \theta^T H \Delta \theta\]To minimize this quadratic approximation, set the derivative w.r.t. \(\Delta \theta\) to zero:
\[\nabla f(\theta) + H \Delta \theta = 0\]Solving gives:
\[\Delta \theta = - H^{-1} \nabla f(\theta)\]This is Newton’s update step.
Numerical Example: Newton’s Method on a Simple 2D Quadratic
Let’s apply this to a concrete function:
Function:
\[f(x_1, x_2) = x_1^2 + 4x_2^2 - 4x_1 - 8x_2\]This is a convex quadratic with an obvious minimum.
- Step 1: Compute Gradient
- Step 2: Compute Hessian
Note: it’s constant since the function is quadratic.
- Step 3: Choose Starting Point
Let’s start at \(x = \begin{bmatrix} 0 \\ 0 \end{bmatrix}\)
- Step 4: Compute Gradient at Starting Point
- Step 5: Newton Step
Use:
\[x_{\text{new}} = x - H^{-1} \cdot \nabla f(x)\]We compute:
– Inverse of Hessian:
\[H^{-1} = \begin{bmatrix} 1/2 & 0 \\ 0 & 1/8 \end{bmatrix}\]– Step:
\[\Delta x = - H^{-1} \cdot \begin{bmatrix} -4 \\ -8 \end{bmatrix} = \begin{bmatrix} 2 \\ 1 \end{bmatrix}\]– Update:
\[x_{\text{new}} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 2 \\ 1 \end{bmatrix} = \begin{bmatrix} 2 \\ 1 \end{bmatrix}\]- Step 6: Verify Minimum
Compute gradient at \(x = [2,\ 1]\):
\[\nabla f(2, 1) = \begin{bmatrix} 0 \\ 0 \end{bmatrix}\]We’ve reached the global minimum in one step.
Gradient Descent vs. Newton’s Method
| Method | Step Formula | Pros | Cons |
|---|---|---|---|
| Gradient Descent | $$x_{t+1} = x_t - \eta \nabla f(x_t)$$ | Simple, stable, scalable | Slow in flat regions; ignores curvature |
| Newton’s Method | $$x_{t+1} = x_t - H^{-1} \nabla f(x_t)$$ | Fast (quadratic convergence near min) | Requires Hessian and matrix inversion |
Newton’s method isn’t widely used in deep learning—because computing and inverting the Hessian is expensive—but it informs the design of many second-order approximations like:
- L-BFGS
- Adam (which estimates 2nd-order behavior via momentum + variance)
- Natural gradient methods
Wrapping Up
We’ve covered a lot of ground—from gradients and directional derivatives to Jacobians and Hessians. At first glance, these might seem like purely academic tools—concepts you meet in a calculus course, solve a few problems with, and move on.
But once you start building machine learning models—especially the kind that don’t behave like nice, neat bowls—you realize: this math doesn’t go away. It just gets buried behind high-level APIs and layers of abstraction.
- Gradients tell us which way to move.
- Jacobians explain how outputs stretch and shift.
- Hessians warn us when the slope changes shape.
These are the core machinery behind optimization, training stability, learning rates, and even architecture design.
What’s powerful is that once you really get these ideas—not just the equations, but the geometry behind them—you start to see why models behave the way they do. Why gradients vanish in one layer and explode in another. Why some loss surfaces feel like gentle slopes and others like twisted ravines. Why second-order methods aren’t used much in deep learning, but still shape the thinking behind optimizers like Adam or AdaGrad.