Convexity, Constraints & Convergence Guarantees
- Convex Functions: Definition and Geometry
- Convex Sets and Jensen’s Inequality
- First-Order and Second-Order Tests for Convexity
- Global vs. Local Minima
- Lagrange Multipliers
- Karush-Kuhn-Tucker (KKT) Conditions
- Applications
- Conclusion
Convexity lies at the heart of modern optimization. Whether you’re minimizing loss in a machine learning model, tuning hyperparameters under constraints, or allocating capital across a portfolio, convexity determines whether your solution is tractable, unique, and efficiently computable.
This blog focuses on the fundamental role that convexity plays in optimization theory and its practical implications in data science and applied machine learning. We will explore:
- How convex functions and convex sets enable global guarantees,
- Why first- and second-order conditions matter for verifying convexity,
- How duality and constraint handling techniques such as Lagrange multipliers and KKT conditions generalize unconstrained problems,
- And how these principles underpin robust optimization in support vector machines, regularized regression, and portfolio allocation.
Throughout, we’ll connect theory to implementation, showing how each result translates to convergence guarantees or algorithm design in real models.
Convex Functions: Definition and Geometry
Convex functions form the foundation of optimization theory. Their structure guarantees that local minima are global minima, making optimization algorithms more reliable and efficient.
Formal Definition
A function \(f : \mathbb{R}^n \to \mathbb{R}\) is said to be convex if, for all \(\mathbf{x}, \mathbf{y} \in \text{dom}(f)\) and for all \(\lambda \in [0, 1]\):
\[f(\lambda \mathbf{x} + (1 - \lambda) \mathbf{y}) \leq \lambda f(\mathbf{x}) + (1 - \lambda) f(\mathbf{y})\]This is known as the convexity inequality.
In words:
The function evaluated at a convex combination of two points is no greater than the convex combination of the function values at those points.
If equality holds throughout, the function is called affine.
Geometric Interpretation
Geometrically, convexity means that the line segment connecting any two points on the graph of the function lies above the graph itself.
Consider two points \((\mathbf{x}, f(\mathbf{x}))\) and \((\mathbf{y}, f(\mathbf{y}))\). Draw a straight line between them. If the function is convex, the entire line segment will lie above or on the function curve.
This property ensures that:
- There are no “traps” like local minima distinct from the global minimum.
- Gradient-based methods can reliably converge to optimal points without the need for complex global search.
Examples of Convex Functions
- Linear functions: \(f(\mathbf{x}) = \mathbf{a}^\top \mathbf{x} + b\)
- Quadratic functions with positive semidefinite Hessian: \(f(\mathbf{x}) = \mathbf{x}^\top Q \mathbf{x} + \mathbf{b}^\top \mathbf{x} + c\) where \(Q \succeq 0\)
- Norms: \(\|\mathbf{x}\|_2\), \(\|\mathbf{x}\|_1\)
- Exponential function: \(f(x) = e^x\)
Visualization
To better illustrate the geometric property of convex functions, we now visualize an example function. The plots below confirm that any line segment between two points on the curve lies entirely above the graph, verifying convexity.
import numpy as np
import matplotlib.pyplot as plt
# Define a convex function
x = np.linspace(-3, 3, 200)
y = np.exp(0.5 * x) + 0.5 * x**2 # Convex combination: exponential + quadratic
# Plot
plt.figure(figsize=(8, 5))
plt.plot(x, y, label='Convex Function', color='blue')
plt.title('Example of a Convex Function')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.grid(True)
plt.legend()
plt.tight_layout()
plt.show()
In this plot:
- The curve is smooth and continuously bends upward.
- Any line segment connecting two points on the graph lies above the curve, verifying convexity.
Convexity not only simplifies optimization theoretically but also ensures practical algorithms can converge efficiently without getting trapped in suboptimal regions.
Convex Sets and Jensen’s Inequality
Convex sets are the geometric foundation of convex analysis. Just as convex functions simplify optimization by ensuring local minima are global, convex sets simplify feasible regions, constraints, and geometric interpretations of optimization problems.
Convex Sets: Definition
A set \(C \subseteq \mathbb{R}^n\) is called convex if for any two points \(\mathbf{x}, \mathbf{y} \in C\) and for any \(\lambda \in [0, 1]\), the point
\[\lambda \mathbf{x} + (1 - \lambda) \mathbf{y}\]also belongs to \(C\).
In words:
Any line segment between two points in the set lies entirely within the set.
This definition directly mirrors the definition of a convex function but applies to sets instead of function graphs.
Examples of Convex Sets
- Euclidean spaces: The entire \(\mathbb{R}^n\) is convex.
- Balls and spheres: The set \(\{\mathbf{x} : \|\mathbf{x}\|_2 \leq r\}\) is convex.
- Halfspaces: Sets defined by linear inequalities \(\mathbf{a}^\top \mathbf{x} \leq b\) are convex.
- Polyhedra: Intersections of a finite number of halfspaces.
In contrast, non-convex sets have “holes,” “bends,” or “gaps” where line segments between points may leave the set.
Visualization of a Convex vs Non-Convex Set
Before we formalize Jensen’s inequality, it’s helpful to visualize the distinction between convex and non-convex sets.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Polygon
# Convex set
convex_points = np.array([[0, 0], [2, 0], [1, 2]])
# Non-convex set
non_convex_points = np.array([[0, 0], [2, 0], [1, 0.5], [1, 2]])
fig, axes = plt.subplots(1, 2, figsize=(12, 5))
# Convex set
axes[0].set_title('Convex Set')
polygon = Polygon(convex_points, closed=True, color='lightblue')
axes[0].add_patch(polygon)
axes[0].plot(convex_points[:, 0], convex_points[:, 1], 'ko-')
axes[0].set_xlim(-1, 3)
axes[0].set_ylim(-1, 3)
axes[0].set_aspect('equal')
axes[0].grid(True)
# Non-convex set
axes[1].set_title('Non-Convex Set')
polygon = Polygon(non_convex_points, closed=True, color='salmon')
axes[1].add_patch(polygon)
axes[1].plot(non_convex_points[:, 0], non_convex_points[:, 1], 'ko-')
axes[1].set_xlim(-1, 3)
axes[1].set_ylim(-1, 3)
axes[1].set_aspect('equal')
axes[1].grid(True)
plt.tight_layout()
plt.show()
- In the convex set, any two points connected by a straight line stay entirely within the set.
- In the non-convex set, there exist points where the connecting line passes outside the set.
This geometric property is fundamental when defining feasible regions for constrained optimization.
Jensen’s Inequality
Formal Statement
Let \(f : \mathbb{R} \to \mathbb{R}\) be a convex function and let \(X\) be a random variable such that \(\mathbb{E}[X]\) and \(\mathbb{E}[f(X)]\) exist.
Then Jensen’s inequality states:
\[f(\mathbb{E}[X]) \leq \mathbb{E}[f(X)]\]In words:
The function applied to the expectation is less than or equal to the expectation of the function.
The inequality reverses if \(f\) is concave.
Intuitive Interpretation
- For convex functions: “Taking the average first and then applying the function” gives a value lower than “applying the function first and then averaging.”
- For concave functions: The inequality is reversed.
This reflects the shape of convex functions: they “bend upward,” so averaging first gives a smaller value than bending individually and averaging.
Simple Example
Suppose \(f(x) = x^2\), a convex function. Let’s take two values:
- \(X\) takes values \(2\) and \(4\) with equal probability \(0.5\).
Then:
- \[\mathbb{E}[X] = 0.5 \times 2 + 0.5 \times 4 = 3\]
- \[f(\mathbb{E}[X]) = (3)^2 = 9\]
Now compute:
\[\mathbb{E}[f(X)] = 0.5 \times (2)^2 + 0.5 \times (4)^2 = 0.5 \times 4 + 0.5 \times 16 = 2 + 8 = 10\]Thus:
\[f(\mathbb{E}[X]) = 9 \leq 10 = \mathbb{E}[f(X)]\]Jensen’s inequality holds.
Geometric Understanding
Visually, if you plot a convex function, and mark two points on the curve, the straight line connecting them lies above the curve.
Thus:
- The function applied to the mean (midpoint) lies below the mean of function values (the line segment connecting function outputs).
This is geometrically consistent with convexity.
Mathematical Proof Sketch (for Discrete Variables)
Suppose \(X\) takes values \(x_1, x_2, \dots, x_n\) with probabilities \(p_1, p_2, \dots, p_n\).
Then:
\[\mathbb{E}[X] = \sum_{i=1}^n p_i x_i\]and
\[\mathbb{E}[f(X)] = \sum_{i=1}^n p_i f(x_i)\]By convexity of \(f\), for each \(x_i\):
\[f\left(\sum_{i=1}^n p_i x_i\right) \leq \sum_{i=1}^n p_i f(x_i)\]Thus:
\[f(\mathbb{E}[X]) \leq \mathbb{E}[f(X])\]Why Jensen’s Inequality Matters
In optimization, statistics, and machine learning:
- It bounds expectations of convex loss functions.
- It guarantees convexity when moving to expected risk formulations (e.g., in empirical risk minimization).
- It explains regularization effects in probabilistic models.
- It plays a crucial role in deriving dual problems and strong duality results.
In many algorithms, particularly in stochastic optimization and variational inference, Jensen’s inequality underpins the movement between expectations and optimization.
First-Order and Second-Order Tests for Convexity
In optimization and convex analysis, it is often necessary to verify whether a given function is convex. Rather than checking the definition directly for every pair of points, we rely on differential conditions—the first-order and second-order tests for convexity.
These conditions provide practical tools for certifying convexity, especially when functions are differentiable or twice-differentiable.
First-Order Condition for Convexity
Theorem (First-Order Convexity Test):
Suppose \(f: \mathbb{R}^n \to \mathbb{R}\) is differentiable. Then \(f\) is convex if and only if, for all \(\mathbf{x}, \mathbf{y} \in \text{dom}(f)\):
Interpretation:
- The function always lies above its tangent hyperplane at any point \(\mathbf{x}\).
- In geometric terms, the graph of \(f\) is “supported from below” by its tangents.
Consequences:
- The gradient at a point provides a global underestimator of the function.
- For linear functions (where the inequality becomes an equality), the function is affine, which is a special case of convexity.
Second-Order Condition for Convexity
Theorem (Second-Order Convexity Test):
Suppose \(f: \mathbb{R}^n \to \mathbb{R}\) is twice differentiable. Then:
- \(f\) is convex if and only if its Hessian matrix \(\nabla^2 f(\mathbf{x})\) is positive semidefinite for all \(\mathbf{x} \in \text{dom}(f)\).
Mathematically:
\[\nabla^2 f(\mathbf{x}) \succeq 0 \quad \text{for all } \mathbf{x}\]Meaning: for all vectors \(\mathbf{z} \in \mathbb{R}^n\),
\[\mathbf{z}^\top \nabla^2 f(\mathbf{x}) \mathbf{z} \geq 0\]Interpretation:
- The curvature of \(f\), as measured along any direction \(\mathbf{z}\), is non-negative.
- The function “bends upward” in every direction.
Practical Summary
| Test | When Applicable | What to Check |
|---|---|---|
| First-Order Test | Differentiable functions | Function lies above its tangent hyperplane at any point |
| Second-Order Test | Twice differentiable functions | Hessian matrix is positive semidefinite everywhere |
For most optimization problems involving twice-differentiable losses (such as in regression, support vector machines, or maximum likelihood estimation), second-order tests are the standard tool.
Example: Verifying Convexity
Consider the function:
\[f(x_1, x_2) = 3x_1^2 + 2x_1x_2 + 4x_2^2\]We want to check: Is this function convex over \(\mathbb{R}^2\)?
Step 1: Compute the Gradient
First, find the gradient vector:
\[\nabla f(x_1, x_2) = \begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \end{bmatrix}\]Calculate partial derivatives:
- \[\frac{\partial f}{\partial x_1} = 6x_1 + 2x_2\]
- \[\frac{\partial f}{\partial x_2} = 2x_1 + 8x_2\]
Thus:
\[\nabla f(x_1, x_2) = \begin{bmatrix} 6x_1 + 2x_2 \\ 2x_1 + 8x_2 \end{bmatrix}\]Step 2: Compute the Hessian Matrix
The Hessian matrix is:
\[\nabla^2 f(x_1, x_2) = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1 \partial x_2} \\ \frac{\partial^2 f}{\partial x_2 \partial x_1} & \frac{\partial^2 f}{\partial x_2^2} \end{bmatrix}\]Compute second partial derivatives:
- \[\frac{\partial^2 f}{\partial x_1^2} = 6\]
- \[\frac{\partial^2 f}{\partial x_1 \partial x_2} = 2\]
- \[\frac{\partial^2 f}{\partial x_2 \partial x_1} = 2\]
- \[\frac{\partial^2 f}{\partial x_2^2} = 8\]
Thus:
\[\nabla^2 f(x_1, x_2) = \begin{bmatrix} 6 & 2 \\ 2 & 8 \end{bmatrix}\]Notice: the Hessian is constant, i.e., independent of \((x_1, x_2)\). This often happens for quadratic functions.
Step 3: Apply the Second-Order Test (Check Positive Semidefiniteness)
A symmetric matrix is positive semidefinite (PSD) if:
- All its eigenvalues are non-negative
- Alternatively, its leading principal minors are non-negative
We check eigenvalues:
Find eigenvalues \(\lambda\) from:
\[\det(\nabla^2 f - \lambda I) = 0\]That is:
\[\det \begin{bmatrix} 6 - \lambda & 2 \\ 2 & 8 - \lambda \end{bmatrix} = 0\]Expand determinant:
\((6-\lambda)(8-\lambda) - (2)(2) = 0\) \(48 - 6\lambda - 8\lambda + \lambda^2 - 4 = 0\) \(\lambda^2 - 14\lambda + 44 = 0\)
Solve:
\(\lambda = \frac{14 \pm \sqrt{196 - 176}}{2} = \frac{14 \pm \sqrt{20}}{2}\) \(\lambda = \frac{14 \pm 2\sqrt{5}}{2} = 7 \pm \sqrt{5}\)
Thus:
- \[\lambda_1 = 7 + \sqrt{5} \approx 9.236\]
- \[\lambda_2 = 7 - \sqrt{5} \approx 4.764\]
Both eigenvalues are positive, so:
\[\nabla^2 f \succeq 0\]Conclusion: The Hessian is positive definite. Thus, the function \(f(x_1, x_2)\) is strictly convex over \(\mathbb{R}^2\).
- We verified convexity using the second-order condition.
- No need to check the convexity inequality manually for all points.
- Since the Hessian is positive definite, \(f\) has a unique global minimum.
- Any optimization algorithm minimizing \(f\) (like gradient descent, Newton’s method) will converge globally.
Global vs. Local Minima
One of the central challenges in optimization is understanding the nature of the solution landscape. Specifically, distinguishing between local minima and global minima is crucial for ensuring whether an optimization algorithm has found the best possible solution.
Convexity simplifies this question dramatically: for convex functions, any local minimum is automatically a global minimum. Without convexity, optimization problems become inherently harder.
Formal Definitions
- Local Minimum:
A point \(\mathbf{x}^\star\) is a local minimum of a function \(f\) if there exists a neighborhood \(\mathcal{N}(\mathbf{x}^\star)\) such that:
- Global Minimum:
A point \(\mathbf{x}^\star\) is a global minimum if:
Key Property of Convex Functions
If \(f\) is convex, then every local minimum is also a global minimum.
More precisely:
- If \(\nabla f(\mathbf{x}^\star) = 0\) (stationary point) for a convex function, then \(\mathbf{x}^\star\) is a global minimizer.
This is one of the most important results in convex optimization—it removes the need for complex global search strategies.
Examples
Convex Example:
\[f(x) = x^2\]- Unique minimum at \(x = 0\)
- The minimum is both local and global.
Non-Convex Example:
\[f(x) = \sin(x)\]over \([0, 4\pi]\):
- Multiple local minima.
- Only one global minimum at the lowest point.
Visual Understanding
- For non-convex functions, there can be many local minima, and finding the global minimum requires sophisticated exploration (e.g., simulated annealing, stochastic gradient descent with restarts).
- For convex functions, the optimization landscape is “bowl-shaped” — any local descent leads directly to the global minimum.
import numpy as np
import matplotlib.pyplot as plt
# Define functions
x_convex = np.linspace(-2, 2, 200)
y_convex = x_convex**2
x_nonconvex = np.linspace(0, 4*np.pi, 400)
y_nonconvex = np.sin(x_nonconvex)
# Plot
fig, axes = plt.subplots(1, 2, figsize=(15, 5))
# Convex function plot
axes[0].plot(x_convex, y_convex, color='blue', label='$f(x) = x^2$')
axes[0].scatter(0, 0, color='red', label='Global Minimum', zorder=5)
axes[0].set_title('Convex Function')
axes[0].set_xlabel('x')
axes[0].set_ylabel('f(x)')
axes[0].legend()
axes[0].grid(True)
# Non-convex function plot
axes[1].plot(x_nonconvex, y_nonconvex, color='orange', label='$f(x) = \\sin(x)$')
# Local minima for sin(x) — multiple
axes[1].scatter([3*np.pi/2, 7*np.pi/2], [-1, -1], color='green', label='Local Minima', zorder=5)
axes[1].set_title('Non-Convex Function')
axes[1].set_xlabel('x')
axes[1].set_ylabel('f(x)')
axes[1].legend()
axes[1].grid(True)
plt.tight_layout()
plt.show()
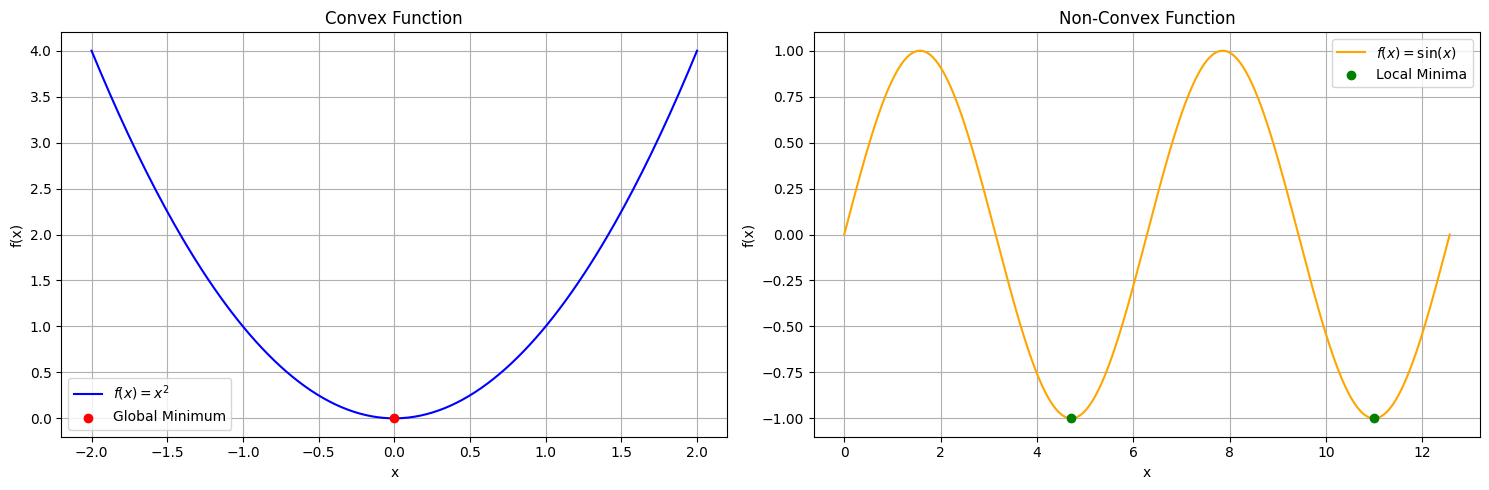
- In the convex function \(f(x) = x^2\), the unique stationary point at \(x=0\) is the global minimum.
- In the non-convex function \(f(x) = \sin(x)\), there are multiple local minima, no unique global minimum.
This visualization makes the distinction between local and global minima immediately apparent.
Practical Implications
| Property | Convex Functions | Non-Convex Functions |
|---|---|---|
| Local Minimum | Always Global | May not be Global |
| Optimization Complexity | Easy (First-Order Methods Succeed) | Hard (Requires Global Methods) |
| Solution Guarantees | Strong | Weak without Extra Structure |
How This Impacts Optimization Algorithms
- In convex optimization (e.g., logistic regression, SVMs), gradient descent, Newton’s method, BFGS converge reliably to the global minimum.
- In non-convex optimization (e.g., deep learning, non-linear programming), local minima, saddle points, and bad critical points are a major concern.
Understanding whether the objective function is convex fundamentally changes how we design and analyze optimization algorithms.
Lagrange Multipliers
Optimization problems often involve constraints.
While unconstrained optimization focuses on stationary points where the gradient vanishes, constrained problems require a different approach: one that respects both the objective function and the constraint surfaces.
Lagrange multipliers provide a systematic way to solve constrained optimization problems by incorporating the constraints directly into the optimization process.
Problem Setting
Consider the following constrained optimization problem:
\[\begin{aligned} \text{minimize} \quad & f(\mathbf{x}) \\ \text{subject to} \quad & h(\mathbf{x}) = 0 \end{aligned}\]where:
- \(f : \mathbb{R}^n \to \mathbb{R}\) is the objective function,
- \(h : \mathbb{R}^n \to \mathbb{R}\) is the constraint function.
Both \(f\) and \(h\) are assumed to be continuously differentiable.
The Lagrangian
We define the Lagrangian function:
\[\mathcal{L}(\mathbf{x}, \lambda) = f(\mathbf{x}) + \lambda h(\mathbf{x})\]where:
- \(\lambda \in \mathbb{R}\) is the Lagrange multiplier.
The idea is to transform the constrained problem into an unconstrained problem involving both \(\mathbf{x}\) and \(\lambda\).
First-Order Necessary Conditions
At an optimal point \(\mathbf{x}^\star\) satisfying regularity conditions (e.g., constraint qualification), there exists \(\lambda^\star\) such that:
\(\nabla_{\mathbf{x}} \mathcal{L}(\mathbf{x}^\star, \lambda^\star) = 0\) \(h(\mathbf{x}^\star) = 0\)
Expanded:
- Stationarity: The gradient of \(f\) at \(\mathbf{x}^\star\) must be a linear combination of the gradients of the constraints.
- Primal feasibility: The constraint must be satisfied.
In other words:
The gradient of the objective is aligned with the gradient of the constraint.
Geometric Interpretation
- In unconstrained optimization, the optimal point satisfies \(\nabla f = 0\).
- In constrained optimization, \(\nabla f\) is not necessarily zero, but it must be normal (perpendicular) to the feasible set at the point of tangency.
The constraint surface \(h(\mathbf{x}) = 0\) defines a manifold, and at the optimum, the direction of steepest descent of \(f\) must be blocked by the constraint boundary.
Example
Solve:
\[\begin{aligned} \text{minimize} \quad & f(x, y) = x^2 + y^2 \\ \text{subject to} \quad & x + y - 1 = 0 \end{aligned}\]Step 1: Form the Lagrangian
\[\mathcal{L}(x, y, \lambda) = x^2 + y^2 + \lambda (x + y - 1)\]Step 2: Compute Partial Derivatives
Stationarity:
\(\frac{\partial \mathcal{L}}{\partial x} = 2x + \lambda = 0\) \(\frac{\partial \mathcal{L}}{\partial y} = 2y + \lambda = 0\)
Primal feasibility:
\[x + y - 1 = 0\]Step 3: Solve the System
From stationarity:
\(2x + \lambda = 0 \quad \Rightarrow \quad \lambda = -2x\) \(2y + \lambda = 0 \quad \Rightarrow \quad \lambda = -2y\)
Thus:
\[x = y\]Substitute into constraint:
\[x + x = 1 \quad \Rightarrow \quad x = \frac{1}{2}, \quad y = \frac{1}{2}\]Thus:
\[(x^\star, y^\star) = \left( \frac{1}{2}, \frac{1}{2} \right)\]and:
\[\lambda^\star = -2x^\star = -1\]At the solution:
- The constraint \(x + y = 1\) is satisfied.
- The contours of \(f(x, y) = x^2 + y^2\) are tangent to the constraint line at \((1/2, 1/2)\).
- The Lagrange multiplier \(\lambda^\star = -1\) measures how much the objective function would improve (decrease) per unit relaxation of the constraint.
import numpy as np
import matplotlib.pyplot as plt
# Grid
x = np.linspace(-0.5, 1.5, 400)
y = np.linspace(-0.5, 1.5, 400)
X, Y = np.meshgrid(x, y)
Z = X**2 + Y**2 # Objective: x² + y²
# Plot
fig, ax = plt.subplots(figsize=(7, 6))
# Objective contours
contours = ax.contour(X, Y, Z, levels=10, cmap='Blues', alpha=0.7)
ax.clabel(contours, inline=True, fontsize=8)
# Constraint line: x + y = 1
y_constraint = 1 - x
ax.plot(x, y_constraint, color='red', label='$x + y = 1$ (Constraint)')
# Mark the optimal point
ax.plot(0.5, 0.5, 'ro', label='Optimal Point $(\\frac{1}{2}, \\frac{1}{2})$')
# Styling
ax.set_title('Lagrange Multipliers: Tangency of Objective and Constraint')
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_xlim(-0.2, 1.2)
ax.set_ylim(-0.2, 1.2)
ax.legend()
ax.grid(True)
plt.tight_layout()
plt.show()
Key Insights
| Aspect | Role of Lagrange Multipliers |
|---|---|
| Gradient Alignment | $$\nabla f(x^\star) = -\lambda \nabla h(x^\star)$$ |
| Incorporating Constraints | Converts constrained optimization into stationary conditions |
| Economic Interpretation | Multipliers represent sensitivity to constraint relaxation |
Karush-Kuhn-Tucker (KKT) Conditions
The Karush-Kuhn-Tucker (KKT) conditions generalize the method of Lagrange multipliers to problems involving inequality constraints.
They are the necessary conditions for optimality in a broad class of optimization problems and form the foundation for constrained optimization theory in data science, machine learning, and operations research.
Problem Setting
Consider the general constrained optimization problem:
\[\begin{aligned} \text{minimize} \quad & f(\mathbf{x}) \\ \text{subject to} \quad & f_i(\mathbf{x}) \leq 0, \quad i = 1, \dotsc, m \\ & h_j(\mathbf{x}) = 0, \quad j = 1, \dotsc, p \end{aligned}\]where:
- \(f(\mathbf{x})\) is the objective function,
- \(f_i(\mathbf{x})\) are inequality constraint functions,
- \(h_j(\mathbf{x})\) are equality constraint functions.
The Lagrangian
We define the Lagrangian:
\[\mathcal{L}(\mathbf{x}, \boldsymbol{\lambda}, \boldsymbol{\nu}) = f(\mathbf{x}) + \sum_{i=1}^m \lambda_i f_i(\mathbf{x}) + \sum_{j=1}^p \nu_j h_j(\mathbf{x})\]where:
- \(\lambda_i \geq 0\) are the Lagrange multipliers for inequality constraints,
- \(\nu_j\) are the multipliers for equality constraints.
KKT Conditions
Suppose \(\mathbf{x}^\star\) is a local minimum and regularity conditions (constraint qualification) hold.
Then there exist \(\boldsymbol{\lambda}^\star, \boldsymbol{\nu}^\star\) such that:
-
Stationarity:
\(\nabla f(\mathbf{x}^\star) + \sum_{i=1}^m \lambda_i^\star \nabla f_i(\mathbf{x}^\star) + \sum_{j=1}^p \nu_j^\star \nabla h_j(\mathbf{x}^\star) = 0\) -
Primal feasibility:
\(f_i(\mathbf{x}^\star) \leq 0, \quad h_j(\mathbf{x}^\star) = 0\) -
Dual feasibility:
\(\lambda_i^\star \geq 0\) -
Complementary slackness:
\(\lambda_i^\star f_i(\mathbf{x}^\star) = 0\)
Intuitive Interpretation
| Condition | Meaning |
|---|---|
| Stationarity | No descent direction combining objective and constraints |
| Primal Feasibility | Constraints are satisfied |
| Dual Feasibility | Multipliers for inequalities are non-negative |
| Complementary Slackness | Either a constraint is active ($$f_i=0$$) or its multiplier is zero |
At the optimum:
- If an inequality constraint is active (\(f_i(\mathbf{x}^\star) = 0\)), its associated \(\lambda_i^\star\) can be positive.
- If a constraint is inactive (\(f_i(\mathbf{x}^\star) < 0\)), its associated \(\lambda_i^\star = 0\).
Simple Example
Solve:
\[\begin{aligned} \text{minimize} \quad & f(x) = x^2 \\ \text{subject to} \quad & x \geq 1 \end{aligned}\]Step 1: Form the Lagrangian
\[\mathcal{L}(x, \lambda) = x^2 + \lambda (1 - x)\]Step 2: KKT Conditions
- Stationarity:
- Primal feasibility:
- Dual feasibility:
- Complementary slackness:
Step 3: Solve
From complementary slackness:
- Either \(x = 1\) or \(\lambda = 0\).
Suppose \(x = 1\):
- Then \(\lambda = 2(1) = 2\) (positive, dual feasible).
Thus:
- \[x^\star = 1\]
- \[\lambda^\star = 2\]
Optimal solution: \(x=1\) minimizing \(f(x)=1\), with active constraint.
Why KKT Conditions Matter
| Aspect | Role of KKT Conditions |
|---|---|
| Handling Inequalities | Extends Lagrange method to inequality constraints |
| Solution Certification | Provides necessary conditions for optimality |
| Algorithms | Basis of modern solvers like interior-point and active-set methods |
Applications
Throughout this blog, we have developed the theoretical machinery necessary to understand convexity, constraints, and optimization guarantees.
In this final part, we connect the theory back to its real-world implementations.
Methods like support vector machines, logistic regression, portfolio optimization, and resource allocation rely on convex problem structures to ensure efficient, reliable, and interpretable solutions.
We now move toward case studies where convexity, Lagrangian duality, and the Karush-Kuhn-Tucker conditions directly power practical models.
Application 1: Solving Constrained Problems: Support Vector Machines (SVM)
Support Vector Machines (SVMs) are a classic case where convex optimization with constraints appears naturally in a machine learning model.
The problem of finding the best linear separator between two classes can be formulated exactly as a convex optimization problem with inequality constraints.
Convexity ensures the existence of a unique, globally optimal solution, and KKT conditions guide us in solving it.
Hard-Margin SVM: Problem Formulation
Suppose we are given a training dataset:
\[\{(\mathbf{x}_i, y_i)\}_{i=1}^n\]where:
- \(\mathbf{x}_i \in \mathbb{R}^d\) are feature vectors,
- \(y_i \in \{-1, +1\}\) are binary labels.
The goal is to find a hyperplane:
\[\mathbf{w}^\top \mathbf{x} + b = 0\]that separates the two classes with the maximum margin.
Optimization Problem
Mathematically, the hard-margin SVM solves:
\[\begin{aligned} \text{minimize} \quad & \frac{1}{2} \|\mathbf{w}\|^2 \\ \text{subject to} \quad & y_i(\mathbf{w}^\top \mathbf{x}_i + b) \geq 1, \quad \forall i \end{aligned}\]Why This Formulation?
- Objective \(\frac{1}{2}\|\mathbf{w}\|^2\) minimizes the norm of \(\mathbf{w}\), which maximizes the margin (distance between the classes).
- Constraints \(y_i(\mathbf{w}^\top \mathbf{x}_i + b) \geq 1\) enforce correct classification of each point with a margin of at least 1.
Thus, finding the hyperplane becomes a constrained quadratic optimization problem.
Constructing the Lagrangian
To incorporate the constraints into the optimization, we introduce Lagrange multipliers \(\lambda_i \geq 0\) for each constraint.
The Lagrangian is:
\[\mathcal{L}(\mathbf{w}, b, \boldsymbol{\lambda}) = \frac{1}{2} \|\mathbf{w}\|^2 - \sum_{i=1}^n \lambda_i \left( y_i(\mathbf{w}^\top \mathbf{x}_i + b) - 1 \right)\]Here:
- The first term is the original objective,
- The second term penalizes violations of the margin constraint using \(\lambda_i\).
Applying the KKT Conditions
At the solution, the following KKT conditions must hold:
1. Stationarity
The gradient of the Lagrangian with respect to \(\mathbf{w}\) and \(b\) must vanish:
- Derivative with respect to \(\mathbf{w}\):
Thus:
\[\mathbf{w} = \sum_{i=1}^n \lambda_i y_i \mathbf{x}_i\]- Derivative with respect to \(b\):
Thus:
\[\sum_{i=1}^n \lambda_i y_i = 0\]2. Primal Feasibility
The original constraints must be satisfied:
\[y_i(\mathbf{w}^\top \mathbf{x}_i + b) \geq 1\]for all training points.
3. Dual Feasibility
The multipliers must be non-negative:
\[\lambda_i \geq 0\]for each \(i\).
4. Complementary Slackness
For each training point:
\[\lambda_i \left( y_i(\mathbf{w}^\top \mathbf{x}_i + b) - 1 \right) = 0\]Meaning:
- If \(\lambda_i > 0\), the corresponding constraint is active (tight): the point lies exactly on the margin.
- If \(\lambda_i = 0\), the point lies outside the margin (not a support vector).
Deriving the Dual Problem
Using the KKT stationarity conditions, we eliminate \(\mathbf{w}\) and obtain the dual problem:
\[\begin{aligned} \text{maximize} \quad & \sum_{i=1}^n \lambda_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \lambda_i \lambda_j y_i y_j \mathbf{x}_i^\top \mathbf{x}_j \\ \text{subject to} \quad & \sum_{i=1}^n \lambda_i y_i = 0 \\ & \lambda_i \geq 0 \end{aligned}\]This dual formulation leads to a convex quadratic programming (QP) problem, which can be efficiently solved using methods such as:
- Sequential Minimal Optimization (SMO) — specialized algorithm for SVMs (used in LIBSVM, scikit-learn).
- Interior-Point Methods — efficient for large, dense QP problems.
- Active-Set Methods — suitable when the number of active constraints (support vectors) is relatively small.
- Projected Gradient Descent — simple method for QPs with non-negativity constraints.
The convexity of the dual problem, guaranteed by the properties of the kernel matrix and Slater’s condition, ensures that any local optimum found by these methods is also a global optimum.
Application 2: Ensuring Convergence in Optimization
The success of optimization algorithms in data science depends not only on problem formulation but also critically on ensuring convergence — that the algorithm reliably approaches an optimal solution within a reasonable number of steps.
In convex optimization, convergence can often be guaranteed under mild conditions.
However, in more general settings, ensuring convergence requires attention to the function structure, algorithm design, and problem constraints.
Why Convergence Guarantees Matter
Without convergence guarantees:
- Algorithms might cycle indefinitely without reaching a solution.
- Solutions might depend heavily on initialization.
- Approximate solutions might lack theoretical bounds on optimality gaps.
Convergence results are essential for both algorithm design and performance certification in practical machine learning workflows.
Core Factors Influencing Convergence
1. Convexity
- If the objective function is convex and constraints define a convex feasible region,
→ Gradient-based methods are guaranteed to converge to a global minimum. - For non-convex problems, convergence may only be to a local minimum or a saddle point.
2. Smoothness
- Functions with Lipschitz-continuous gradients (i.e., gradients that do not change abruptly) enable faster convergence.
- Smooth convex functions allow algorithms like gradient descent to achieve rates like:
where \(k\) is the iteration number.
3. Strong Convexity
- If the function is strongly convex (there exists a lower curvature bound), faster convergence can be achieved:
e.g., exponentially fast convergence for strongly convex functions under gradient descent.
Mathematical Conditions for Convergence
Suppose \(f: \mathbb{R}^n \to \mathbb{R}\) is:
- Convex,
- Differentiable with \(L\)-Lipschitz continuous gradient.
Then for Gradient Descent with step size \(\eta \leq 1/L\):
- The sequence \(\{f(x^{(k)})\}\) satisfies:
where:
- \(x^\star\) is the global minimizer,
- \(x^{(k)}\) is the iterate at step \(k\).
Thus, after \(k\) steps, the suboptimality gap decays as \(\mathcal{O}(1/k)\).
Practical Approaches to Guarantee Convergence
| Strategy | Explanation |
|---|---|
| Proper Step Size Selection | Choose learning rates carefully (fixed, diminishing, or adaptive schemes) |
| Use of Strongly Convex Regularization | Add $$\ell_2$$ penalties (e.g., in ridge regression) to enhance curvature and speed up convergence |
| Constraint Handling | Use projection methods, penalty functions, or barrier methods to maintain feasibility during optimization |
| Variance Reduction Techniques | Apply SVRG, SAG, or SAGA to accelerate convergence in stochastic optimization settings |
| Trust Region Methods | Adaptively restrict step sizes to regions where second-order approximations are valid |
Summary Table: Key Drivers of Convergence
| Condition | Impact on Convergence |
|---|---|
| Convexity | Guarantees global optimality; sublinear convergence rate |
| Strong Convexity | Enables exponential (linear) convergence rate |
| Smoothness (Lipschitz Gradient) | Allows safe step-size selection and stable updates |
| Constraint Qualification | Ensures valid application of KKT conditions |
- In convex problems, convergence is predictable and guaranteed.
- In non-convex settings, convergence needs careful algorithmic design and may only reach local solutions.
- Optimization methods can be tailored by understanding smoothness, strong convexity, and constraints.
Application 3: Convexity in Logistic Regression and Ridge Regression
Convexity plays a crucial role in ensuring that standard supervised learning models like logistic regression and ridge regression are efficiently trainable and guaranteed to converge to global minima.
Both models involve solving convex optimization problems, which provides strong theoretical guarantees and practical algorithmic stability.
Logistic Regression
Problem Setting
Given a binary classification task, logistic regression models the conditional probability as:
\[P(y = 1 \mid \mathbf{x}) = \frac{1}{1 + \exp(-\mathbf{w}^\top \mathbf{x} - b)}\]The objective is to minimize the negative log-likelihood over the dataset:
\[\mathcal{L}(\mathbf{w}, b) = \sum_{i=1}^n \log\left(1 + \exp(-y_i(\mathbf{w}^\top \mathbf{x}_i + b))\right)\]Why the Loss is Convex
- The function \(z \mapsto \log(1 + \exp(-z))\) is convex.
- The composition of a convex function with a linear function (like \(\mathbf{w}^\top \mathbf{x}\)) preserves convexity.
- Thus, \(\mathcal{L}(\mathbf{w}, b)\) is a convex function in \((\mathbf{w}, b)\).
Consequences
| Aspect | Role of Convexity |
|---|---|
| Global Optimality | Any local minimum is global |
| Algorithm Choice | First-order methods (e.g., gradient descent) reliably converge |
| Duality | Dual formulations can be derived if needed (e.g., in kernel logistic regression) |
Ridge Regression
Problem Setting
Ridge regression addresses overfitting in linear models by adding an \(\ell_2\) penalty on the coefficients.
Given inputs \(X \in \mathbb{R}^{n \times d}\) and outputs \(\mathbf{y} \in \mathbb{R}^n\), ridge regression solves:
\[\mathcal{L}(\mathbf{w}) = \|X\mathbf{w} - \mathbf{y}\|_2^2 + \lambda \|\mathbf{w}\|_2^2\]where:
- The first term measures the data fitting (least squares error),
- The second term penalizes large coefficients, and \(\lambda > 0\) controls the strength of regularization.
Why the Loss is Convex
- \(\|X\mathbf{w} - \mathbf{y}\|_2^2\) is a convex quadratic function (positive semidefinite Hessian \(X^\top X\)).
- \(\|\mathbf{w}\|_2^2\) is convex and strongly convex.
- A non-negative weighted sum of convex functions is convex.
Thus, \(\mathcal{L}(\mathbf{w})\) is strongly convex.
Practical Importance of Convexity
| Model | Impact of Convexity |
|---|---|
| Logistic Regression | Guarantees globally optimal classifier under maximum likelihood |
| Ridge Regression | Guarantees unique, stable regression coefficients; improves generalization |
Both models can be solved reliably using standard first-order methods (e.g., gradient descent, coordinate descent) or closed-form solutions (e.g., in ridge regression).
Application 4: Portfolio Optimization and Resource Allocation Problems
Convex optimization frameworks are widely applied in finance (portfolio optimization) and operations research (resource allocation).
Both fields involve finding optimal decisions under constraints, and convexity ensures these problems are tractable, efficiently solvable, and guaranteed to find global solutions.
Portfolio Optimization
Problem Setting
Suppose an investor must allocate wealth across \(n\) assets.
Let:
- \(\mathbf{w} \in \mathbb{R}^n\) denote portfolio weights,
- \(\Sigma\) be the covariance matrix of asset returns,
- \(\mathbf{r}\) be the expected returns vector.
The classic mean-variance optimization problem (Markowitz formulation) is:
\[\begin{aligned} \text{minimize} \quad & \frac{1}{2} \mathbf{w}^\top \Sigma \mathbf{w} \quad \text{(portfolio risk)}\\ \text{subject to} \quad & \mathbf{r}^\top \mathbf{w} \geq r_{\text{target}} \quad \text{(expected return)}\\ & \mathbf{1}^\top \mathbf{w} = 1 \quad \text{(budget constraint)}\\ & w_i \geq 0 \quad \text{(no short-selling)} \end{aligned}\]Why It’s Convex
- The objective \(\mathbf{w}^\top \Sigma \mathbf{w}\) is convex because \(\Sigma\) is a covariance matrix (positive semidefinite).
- Constraints are affine (linear equalities and inequalities).
- Thus, this is a convex quadratic program.
Practical Interpretation
| Aspect | Role |
|---|---|
| Objective | Minimize portfolio risk (variance) |
| Return Constraint | Achieve minimum desired expected return |
| Budget Constraint | Ensure full capital allocation |
| Short-Selling Constraint | Enforce realistic trading conditions |
Convexity ensures:
- Existence of a unique globally optimal portfolio,
- Feasible application of standard solvers (interior-point, active-set methods),
- Stability and robustness to perturbations in market estimates.
Resource Allocation Problems
Resource allocation involves distributing limited resources across competing activities to optimize an objective such as cost, profit, efficiency, or throughput.
Typical structure:
\[\begin{aligned} \text{minimize} \quad & f_0(\mathbf{x}) \quad \text{(cost or loss function)}\\ \text{subject to} \quad & \sum_{i=1}^n x_i = R_{\text{total}} \quad \text{(resource budget)}\\ & x_i \geq 0 \quad \text{(non-negativity)} \end{aligned}\]where:
- \(x_i\) represents resource allocated to task \(i\),
- \(f_0\) is convex (e.g., diminishing returns cost functions).
Examples
- Cloud computing: Allocate server capacity across services to minimize latency.
- Supply chain: Allocate production resources to maximize throughput under cost and time constraints.
- Healthcare: Allocate vaccines across regions to minimize disease spread.
All these settings lead naturally to convex programs when cost, utility, or loss functions are convex.
Summary Table: Convexity in Financial and Resource Optimization
| Application | Optimization Problem | Role of Convexity |
|---|---|---|
| Portfolio Optimization | Minimize risk subject to return and budget constraints | Ensures unique, efficient global solution |
| Resource Allocation | Distribute resources to minimize cost or maximize output | Guarantees optimal, feasible allocations |
Conclusion
Convexity is the structure that transforms optimization from an inherently difficult, potentially unstable task into a mathematically tractable and reliably solvable one.
Throughout this blog, we explored:
- How convex functions and convex sets provide guarantees about local and global optimality,
- How tools like Lagrange multipliers and the Karush-Kuhn-Tucker (KKT) conditions extend optimization to constrained settings,
- How strong duality can be ensured through Slater’s condition,
- And how practical models — from support vector machines to logistic regression, portfolio optimization, and resource allocation — all rely on convexity to ensure convergence, stability, and interpretability.
Optimization frameworks that exploit convexity are central to building models that are not only performant but also provably reliable.
Understanding convex analysis is a necessary part of designing, diagnosing, and improving optimization pipelines across fields.
In modern data science, convexity remains a foundation upon which scalable, reproducible, and robust systems are built.