Applied Probabilistic Modeling

• 1. Probabilistic Graphical Models (PGMs)
  • Bayesian Networks: Structured Reasoning Under Uncertainty
    • Case Study: Medical Diagnosis with a Bayesian Network
  • Conditional Random Fields (CRFs): Structured Prediction in NLP
    • Feature Engineering for CRFs (with Code Example)
  • Inference in PGMs: Exact vs. Approximate
• 2. Copulas: Modeling Complex Dependencies
  • Copula Basics and Sklar’s Theorem
  • Common Copula Families and Dependency Types
  • Fitting and Using Copulas in Practice (with Python)
• 3. Survival Analysis: Time-to-Event Modeling
  • Why Not Treat it as Regression or Classification?
  • The Survival Function and Kaplan-Meier Estimator
  • Cox Proportional Hazards Model
  • Extensions: Competing Risks and Beyond
  • Summing Up Survival Analysis (Use Case: User Retention Modeling)

A few years ago, a large insurance company began rolling out a predictive model to flag potentially fraudulent claims. It was a classic supervised learning problem: train a model on past claims labeled as “fraud” or “not fraud,” and use it to score new ones. The initial version worked reasonably well — accuracy was decent, and stakeholders were optimistic.

But over the months, strange patterns emerged.

Some flagged claims turned out completely legitimate. Others sailed through undetected, only to be uncovered weeks later by auditors. Worse, the model started showing signs of bias — over-flagging claims from a few geographic pockets, under-flagging suspicious ones with clean paperwork. Something wasn’t right.

The issue wasn’t the algorithm. It was the assumptions.

The model assumed each claim was an independent event — just rows in a table. But in reality, claims were connected: a sudden spike in dental reimbursements in one region often hinted at coordinated fraud. Policyholders with similar backgrounds shared risks. Investigators noticed that claim timing, often ignored by the model, carried signals too — many fraudulent actors made their move just before policy expiration.

What the problem needed wasn’t just classification. It needed a probabilistic lens — one that could account for dependencies between variables, hidden influences, and the time it took for things to unfold.

This post is about exactly that shift in perspective — from simple, flat prediction to probabilistic modeling that captures structure, uncertainty, and temporal nuance. We’ll walk through three powerful yet underused tools that bring this perspective to life.

We’ll start with Probabilistic Graphical Models, which let us encode relationships between variables as a network and reason about hidden causes, such as inferring fraud from partial evidence or modeling diseases and symptoms. Then we’ll explore Copulas, a tool for modeling dependencies between variables separately from their distributions — critical in fields like finance and marketing, where things don’t always follow clean, normal rules. Finally, we’ll dive into Survival Analysis, which focuses not just on whether an event will happen, but when — essential for tasks like churn prediction, failure modeling, and clinical studies where some outcomes remain unseen.

Let’s begin.

1. Probabilistic Graphical Models (PGMs)

Imagine you’re building a medical diagnosis system. You have many variables: diseases, symptoms, test results, patient demographics, etc., all influencing each other. How can you model the joint probability over all these variables in a way that’s both mathematically sound and computationally feasible? Probabilistic Graphical Models (PGMs) provide a principled answer.

PGMs combine probability theory and graph theory to represent complex distributions in a compact, intuitive form. Formally, a PGM is a probabilistic model where a graph (nodes = random variables, edges = probabilistic dependencies) encodes the conditional dependence structure. In other words, the graph structure tells us which variables directly influence which others, and this structure enables us to factorize a high-dimensional joint probability distribution into smaller, more manageable pieces. There are two main flavors of PGMs: directed models (often called Bayesian Networks) and undirected models (often called Markov Random Fields; Conditional Random Fields are a special case). We’ll explore both types:

• Bayesian Networks (Directed PGMs) – Great for encoding causal or directional relationships (e.g. \(\text{disease} \rightarrow \text{symptom}\)). They factorize the joint probability into conditional probabilities along the directed acyclic graph (DAG).
• Conditional Random Fields (Undirected PGMs) – Great for sequence labeling and other structured prediction, where we model the conditional distribution of output variables given inputs without assuming a directed generative process.

We’ll also discuss how to perform inference in PGMs – answering queries like “given these symptoms, what’s the probability of a disease?” – using exact and approximate algorithms.

Bayesian Networks: Structured Reasoning Under Uncertainty

A Bayesian Network (BN), or belief network, is a directed acyclic graph (DAG) where each node represents a random variable, and each edge encodes a direct probabilistic influence. If there’s an arrow from node \(A\) to node \(B\), we interpret it as “\(A\) is a parent (direct cause or influence) of \(B\).” Each node has a conditional probability distribution (CPD) specifying \(P(\text{node} \mid \text{its parents})\). The DAG structure implies conditional independence assumptions: each node is independent of its non-descendants given its parents. Thanks to these independencies, the joint probability of all variables factorizes exactly as the product of all local conditional probabilities:

In plain words, a Bayesian network lets us build a big joint distribution by multiplying together lots of small conditional pieces. Each piece is easier to specify and understand. For example, if \(A\) and \(B\) are independent causes of \(C\) in the graph (\(A \rightarrow C \leftarrow B\)), the joint is:

If the graph says \(A \rightarrow B \rightarrow C\), then:

This factorization reflects the conditional independencies encoded by the graph structure.

Case Study: Medical Diagnosis with a Bayesian Network

Let’s return to the medical diagnosis scenario. Suppose we want to model the relationship between a disease and two symptoms. We can create a simple Bayesian network: a node Disease (\(D\)) that has directed arrows to Fever (\(F\)) and Cough (\(C\)). This captures the idea that whether the patient has the disease influences the probabilities of the symptoms.

Here Disease influences the presence of Fever and Cough. The graph encodes that Fever and Cough are conditionally independent given Disease (once we know whether the patient has the disease, the symptoms occur independently).

To fully specify this BN, we need the conditional probability tables:

• \(P(\text{Disease}=1)\) – the prior probability of the disease (say it’s a rare disease: 5%).
• \(P(\text{Fever}=1 \mid \text{Disease})\) and \(P(\text{Fever}=1 \mid \neg\text{Disease})\) – e.g. if diseased, 80% chance of fever; if not, 10% chance of fever.
• \(P(\text{Cough}=1 \mid \text{Disease})\) and \(P(\text{Cough}=1 \mid \neg\text{Disease})\) – e.g. if diseased, 70% chance of cough; if not, 10% chance.

Let’s assign some numbers as an example:

• \(P(D=1) = 0.05\) (5% prevalence of the disease), so \(P(D=0)=0.95\).
• \(P(F=1 \mid D=1) = 0.8\), \(P(F=1 \mid D=0) = 0.1\).
• \(P(C=1 \mid D=1) = 0.7\), \(P(C=1 \mid D=0) = 0.1\).

Using these, the joint distribution factorizes as:

We can compute any query of interest. A common task is inference: e.g., given we observe Fever and Cough, what is the probability the patient has the Disease? This is essentially applying Bayes’ rule using the BN’s probabilities.

Inference Example: Calculate \(P(D=1 \mid F=1, C=1)\). Using the BN:

• The prior odds: \(P(D=1) = 0.05\).
• Likelihood of observing \(F=1, C=1\) if diseased:
  \(P(F=1, C=1 \mid D=1) = 0.8 \times 0.7 = 0.56\) (assuming \(F\) and \(C\) independent given \(D\)).
• Likelihood if not diseased:
  \(P(F=1, C=1 \mid D=0) = 0.1 \times 0.1 = 0.01\).

By Bayes’ rule:

So even though the disease was rare (5%), the presence of both symptoms raises the posterior probability to about 74.7%. This kind of reasoning falls out naturally from a Bayesian network.

We can verify this calculation with a bit of Python code for clarity:

p_d = 0.05
p_f_given_d = 0.8; p_f_given_not_d = 0.1
p_c_given_d = 0.7; p_c_given_not_d = 0.1

# If we observe Fever=1 and Cough=1, compute posterior P(D=1 | F=1, C=1)
num = p_d * p_f_given_d * p_c_given_d
denom = num + (1 - p_d) * p_f_given_not_d * p_c_given_not_d
posterior = num / denom
print(f"Posterior probability of disease given symptoms = {posterior:.3f}")

This prints:

Posterior probability of disease given symptoms = 0.747

Which matches our manual calculation.

Why use a BN instead of just doing Bayes in a table? Because for complex problems, BNs scale much better. Imagine dozens of diseases and symptoms; a full joint table would be enormous, but a BN breaks it into bite-sized conditional tables, leveraging conditional independencies to keep things tractable. BNs are also interpretable – doctors can examine the network structure and CPTs to understand the model’s reasoning.

Bayesian networks are widely used in medical diagnosis, troubleshooting systems, and any domain where causality or dependency structure is important. They were famously used in the early diagnostic tool Quick Medical Reference (QMR) and many modern expert systems. In healthcare, researchers have built BNs for diagnosing cardiac conditions, cancers, etc., by encoding medical knowledge as a graph of influence.

Learning BNs from data: If the structure is not known, algorithms exist to learn both the graph and the CPTs from data (though structure learning is challenging and often NP-hard). But that’s a topic for another day!

Conditional Random Fields (CRFs): Structured Prediction in NLP

While Bayesian networks are generative (modeling full joint distributions, often for causal reasoning), Conditional Random Fields (CRFs) take a discriminative approach, especially useful for tasks like sequence labeling in natural language processing. A CRF is an undirected graphical model (a Markov Random Field) used to model the conditional distribution \(P(\mathbf{Y} \mid \mathbf{X})\) of some output variables \(\mathbf{Y}\) given input features \(\mathbf{X}\). They are most famously applied in scenarios where the outputs have structure (like sequences or grids), for example: part-of-speech tagging, named entity recognition (NER), DNA sequence labeling, or image segmentation.

Why not just use a regular classifier on each element of the sequence? Because neighboring outputs are correlated. For example, in part-of-speech tagging, the tag of a word depends on the tags of its neighboring words (“New” is likely tagged as an adjective if followed by a noun like “York”, but as a proper noun if it’s part of “New York” as a city name). A standard classifier per word wouldn’t account for these dependencies. CRFs were designed to fix that: “Whereas a classifier predicts a label for a single sample without considering neighboring samples, a CRF can take context into account by modeling dependencies between the predictions.” In effect, a CRF looks at the whole sequence of outputs and ensures the predictions are globally consistent with each other and the input features.

Linear-chain CRF (for sequences): The most common CRF is a linear chain, where the output labels \(Y_1, Y_2, \dots, Y_T\) (for a sequence of length \(T\)) form a chain graph (each \(Y_t\) connected to \(Y_{t-1}\) and \(Y_{t+1}\)). The model defines a conditional probability of the entire sequence of labels given the sequence of observations:

where \(f_k\) are feature functions and \(\lambda_k\) are their weights. \(Z(\mathbf{X})\) is the normalization factor (partition function) ensuring the probabilities sum to 1. You can see this is essentially a log-linear model: each possible label sequence \(\mathbf{Y}\) gets a score from weighted feature functions, and we exponentiate and normalize. The feature functions can look at the current label \(Y_t\), the previous label \(Y_{t-1}\), the observation sequence \(\mathbf{X}\) (e.g. the words), and position \(t\). This flexibility is key – we can define rich, overlapping features on the observation without worrying about modeling \(P(\mathbf{X})\) (we only model \(P(\mathbf{Y} \mid \mathbf{X})\)).

Example (NER): Let’s say we want to label each word in a sentence as Person (PER), Location (LOC), or Other (O). A CRF could consider features like:

• The word itself (e.g. is it “John”? then likely PER).
• Is the first letter capitalized?
• The part-of-speech of the word (if available as an input feature).
• Neighboring words (e.g. next word is “Inc.” might indicate current word is an Organization).
• Previous label (the model will learn that if the previous label was B-LOC (beginning of a location), the current label is likely I-LOC (continuation) or O, but not B-PER, for instance).

Unlike an HMM (Hidden Markov Model) which would require a probability distribution of each word given a tag, the CRF can incorporate arbitrary features of the input. It discriminatively learns weights for features that correlate with certain labels, rather than needing to specify a generative story for observations. This often yields higher accuracy in practice for NLP tasks, because you can plug in all sorts of informative signals.

Feature Engineering for CRFs (with Code Example)

To clarify how we feed data into a CRF, let’s walk through preparing features for a toy sequence. Suppose we have a sentence like:

[("John", "NNP", "B-PER"), ("lives", "VBZ", "O"), ("in", "IN", "O"), ("New", "NNP", "B-LOC"), ("York", "NNP", "I-LOC"), (".", ".", "O")]

Here each tuple is (word, POS-tag, NER-label). In training, we have both the input (word, maybe its POS) and the output label. We’ll create a feature dictionary for each word position. A simplified feature extraction might include:

• The lowercase word.
• Whether the word is uppercase or titlecase.
• The word’s POS tag (if we consider POS as an input feature).
• Similarly, features for the previous and next word (to give context).
• Special indicators for beginning of sentence (BOS) or end of sentence (EOS).

Below is a simple function for extracting such features from a sequence, and we’ll apply it to our example sentence:

def word2features(sent, i):
    word = sent[i][0]
    postag = sent[i][1]
    features = {
        'word.lower': word.lower(),
        'is_title': word.istitle(),
        'is_upper': word.isupper(),
        'is_digit': word.isdigit(),
        'postag': postag
    }
    if i == 0:
        features['BOS'] = True  # Beginning of sequence
    else:
        prev_word = sent[i-1][0]; prev_postag = sent[i-1][1]
        features.update({
            'prev.word.lower': prev_word.lower(),
            'prev.postag': prev_postag
        })
    if i == len(sent)-1:
        features['EOS'] = True  # End of sequence
    else:
        next_word = sent[i+1][0]; next_postag = sent[i+1][1]
        features.update({
            'next.word.lower': next_word.lower(),
            'next.postag': next_postag
        })
    return features

# Apply to each word in the example sentence
sentence = [("John","NNP","B-PER"), ("lives","VBZ","O"), ("in","IN","O"),
            ("New","NNP","B-LOC"), ("York","NNP","I-LOC"), (".",".","O")]
X_seq = [word2features(sentence, i) for i in range(len(sentence))]
y_seq = [label for (_, _, label) in sentence]  # the NER labels
print(X_seq[0], "=>", y_seq[0])

Running this might output features for the first word “John”:

{
 'word.lower': 'john',
 'is_title': True,
 'is_upper': False,
 'is_digit': False,
 'postag': 'NNP',
 'BOS': True,
 'next.word.lower': 'lives',
 'next.postag': 'VBZ'
} => B-PER

We see how the features for “John” include itself (lowercased), flags for capitalization, its POS tag NNP (proper noun), a BOS indicator (since John is first word), and some features from the next word (“lives”). The label for this token is B-PER (beginning of a person name). We would create such feature dicts for every token in every training sentence, and feed that to a CRF training algorithm which learns weights \(\lambda_k\) for each feature that best predict the correct labels.

Under the hood, training a CRF often involves maximizing the conditional log-likelihood:

over training examples, which leads to iterative optimization (often using gradient ascent or quasi-Newton methods). Inference (decoding the best label sequence for new input) uses algorithms like Viterbi (for linear-chain CRFs) which are similar to those in HMMs, leveraging dynamic programming to efficiently find the argmax sequence.

Real-world use case: In Natural Language Processing, CRFs became a go-to method for tasks like:

• Part-of-Speech Tagging: assigning noun/verb/adjective/etc to each word. CRFs can incorporate spelling features (e.g., “-ing” ending suggests verb), context, etc.
• Named Entity Recognition: as in the example above, identifying names of people, organizations, locations in text.
• Chunking/Shallow Parsing: grouping words into phrases.
• Bioinformatics: e.g. labeling parts of a gene sequence as coding/non-coding regions.

Even though deep learning has risen, CRFs are still used (sometimes on top of neural network outputs to enforce structured consistency). The key lesson: whenever the output prediction problem has structure (not just independent labels), graphical models like CRFs can significantly improve performance by modeling those output interdependencies.

Inference in PGMs: Exact vs. Approximate

Building a graphical model is only half the battle – we also need to infer probabilities from it. Inference means computing answers to queries like “what is \(P(\text{Disease}=1 \mid \text{Fever}=1, \text{Cough}=1)\)?” or “what labeling of this sequence maximizes \(P(\mathbf{Y} \mid \mathbf{X})\)?” We saw a simple manual inference in the BN example. For small, tree-structured networks, exact inference is feasible via algorithms like variable elimination or belief propagation. However, for arbitrary graphs, exact inference can be extremely expensive – in fact, Cooper proved in 1990 that exact inference in Bayesian networks is NP-hard(more specifically \(\#P\)-hard, which is even worse than NP-complete). This result prompted a lot of research into approximate inference methods.

Here’s an overview of inference approaches:

• Exact Inference:
  • Variable Elimination: A dynamic programming approach that summation-eliminates variables one by one using the factorized representation. It’s efficient if the graph has low treewidth (no huge cliques form during elimination).
  • Belief Propagation (Message Passing): If the graph is a tree (no loops), passing messages along the edges can compute posteriors exactly. In a chain or tree CRF, this is essentially the forward-backward or Viterbi algorithm.
  • Junction Tree Algorithm: For loopy graphs, we can convert the graph into a tree of clusters (a junction tree) and do message passing there. This is exact but can blow up exponentially if the clusters are large.
• Approximate Inference:
  • Sampling (Monte Carlo): Use random samples to estimate probabilities. Gibbs sampling is a popular method for PGMs: iteratively sample each variable from its distribution given the current neighbors, eventually approximating the true joint distribution. Metropolis-Hastings and other MCMC methods also apply.
  • Variational Inference: Turn inference into an optimization problem. The idea is to find a simpler approximate distribution \(Q\) that is close to the true distribution \(P\) (often measured by KL divergence). Mean-field variational inference, for example, assumes an approximate form where variables are independent (or in small groups) and finds parameters that make \(Q\) closest to \(P\). Another variational method is loopy belief propagation, which applies message passing on loopy graphs (not guaranteed exact, but often a good heuristic).
  • Algorithms for specific CRFs: In NLP, if an approximate inference is needed (e.g. in a CRF with long-range dependencies), one might use loopy BP or a truncated beam search for the best sequence, etc. Many CRFs however are designed so that exact inference (Viterbi, forward-backward) is still tractable.

In practice, the approach depends on the problem size and requirements:

• For a small medical BN, exact inference via variable elimination or sampling might be fine.
• For a huge network (hundreds of nodes densely connected), one resorts to sampling or variational approximations.
• For a linear-chain CRF on sequences, we usually use exact dynamic programming (which is polynomial in sequence length and state space size).
• If you have a loopy CRF (like a 2D grid for image segmentation), exact inference is intractable, so people use loopy belief propagation or graph cut approximations.

Key takeaway: Inference is where the “rubber meets the road” for PGMs. Despite the complexity, the structured approach of PGMs often still beats naive methods because it leverages conditional independencies and can incorporate domain knowledge. And even if we approximate, we have a coherent probabilistic framework guiding us.

Before moving on, let’s summarize PGMs:

• They provide a framework for modeling joint distributions compactly using graphs.
• Bayesian Networks handle directed relationships and are great for reasoning under uncertainty (with interpretable causal semantics).
• CRFs (and MRFs) handle undirected relationships, especially useful for conditional modeling of structured outputs.
• Inference can be challenging, but a variety of exact/approximate methods exist; understanding the graph structure is key to choosing the right one.
• Use case recap: We saw a medical diagnosis BN (interpret probabilities of disease given symptoms) and an NLP tagging CRF (label sequences with dependencies).

Armed with PGMs, you can tackle problems involving many interdependent variables in a principled way, rather than resorting to ad-hoc rules. Next, let’s change gears from discrete structures to continuous ones: we’ll discuss Copulas, a tool for modeling complex dependencies between random variables in fields like finance.

2. Copulas: Modeling Complex Dependencies

Have you ever modeled a multivariate dataset assuming a multivariate normal distribution, only to find the marginal distributions aren’t normal at all? Or computed correlation coefficients, but worried they don’t capture extreme co-movements (like simultaneous crashes of multiple stocks)? Copulas are a powerful technique to address such situations. They allow us to model the marginal distribution of each variable separately from the dependence structure between variables. In essence, a copula is a function that “couples” multiple distributions together.

Copula Basics and Sklar’s Theorem

In probability theory, a copula is a multivariate distribution defined on the unit hypercube \([0,1]^d\) with uniform marginals. That means if \((U_1,\dots,U_d)\) is distributed according to a copula \(C\), then each \(U_i \sim \text{Uniform}(0,1)\) individually. The copula’s job is to capture the dependence between the components. Sklar’s Theorem (1959) is the foundational result that makes copulas so useful:

Sklar’s Theorem: For any set of random variables \(X_1,\dots,X_d\) with continuous joint distribution \(F_{X_1,\dots,X_d}\) and marginal CDFs \(F_{X_1},\dots,F_{X_d}\), there exists a copula \(C(u_1,\dots,u_d)\) such that for all \(x_i\):

In simpler terms, any multivariate distribution can be expressed as a copula applied to its marginal distributions. And if the marginals are continuous, this copula is unique. This is extremely powerful: it means we can model margins and dependence separately. Need heavy-tailed marginals (like incomes, financial returns)? No problem, choose appropriate \(F_{X_i}\). Need a certain correlation or tail dependence structure? Choose an appropriate copula \(C\).

Another perspective: if \(U_i = F_{X_i}(X_i)\), i.e., transform each variable to a uniform by its own CDF (often called the probability integral transform), then \((U_1,\dots,U_d)\) has copula \(C\) as its joint CDF. So a copula lives in the transformed “ranks” or “percentile” space of the data.

Key point: Copulas completely describe the dependence structure between variables, independent of the marginals. Two datasets with very different marginal distributions could have the same copula (same dependency pattern).

Common Copula Families and Dependency Types

There are many families of copulas; here are a few important ones:

• Gaussian Copula: Constructed from a multivariate normal distribution. You take a multivariate normal with some correlation matrix \(\Sigma\), and then transform each margin to uniform via the normal CDF. The Gaussian copula is popular because it’s relatively easy to work with (just like correlation matrices), but it has a big limitation: it assumes elliptical dependence and has no tail dependence unless correlation is 1. In fact, one criticism after the 2008 financial crisis was that heavy use of Gaussian copulas in finance underestimated the probability of joint extreme events (like many loans defaulting together). In a Gaussian copula, extreme highs/lows aren’t especially more correlated than moderate values – correlation is the same in all regions.

• t-Copula (Student’s t Copula): Similar to Gaussian but using a multivariate t-distribution. This copula does have tail dependence (the amount depends on the degrees of freedom parameter). It’s often used in finance as an improvement over Gaussian, to allow joint crashes or booms to be more likely than Gaussian would predict.

• Archimedean Copulas: A broad family defined via a generator function; includes popular one-parameter copulas:
  • Clayton copula: Captures lower-tail dependence (i.e., tends to produce joint extreme low values together more than independent would). Often used for modeling variables that have correlated worst-case scenarios.
  • Gumbel copula: Captures upper-tail dependence (correlated high values). Useful if you expect variables to have extreme highs together (e.g., extreme weather variables).
  • Frank copula: Has no particular tail bias, more symmetric.

  Archimedean copulas are easy to construct for any dimension and only use one parameter to govern dependence strength. For example, Clayton’s parameter \(\theta \in [0,\infty)\) (with \(\theta = 0\) meaning independence copula, and higher \(\theta\) = stronger lower-tail linkage).

• Independence copula: A trivial copula \(C(u_1,\dots,u_d) = u_1 \cdots u_d\), which corresponds to variables being independent (the joint CDF factorizes). It’s the baseline with no dependence.

To measure how strong dependence is, one can use metrics like Kendall’s tau or Spearman’s rho which are invariant under monotonic transformations (hence focus on the copula). These are often directly related to copula parameters for one-parameter families. For instance, for a Clayton copula,

Tail Dependence: This concept deserves a bit more explanation. Upper tail dependence \(\lambda_U\) between two variables is the probability that one is at an extreme high quantile given the other is, e.g.,

If \(\lambda_U > 0\), it means they have a tendency to experience extreme highs together. Gaussian copulas have \(\lambda_U = 0\) for any finite correlation less than 1 – so no asymptotic tail linkage; t-copulas have \(\lambda_U > 0\). Lower tail dependence \(\lambda_L\) is defined similarly for the lower end. Archimedean copulas like Clayton have \(\lambda_L > 0\), Gumbel has \(\lambda_U > 0\), etc. When modeling risk, tail dependence is often critical – it answers “if one market crashes, how likely is another to crash at the same time?”.

Fitting and Using Copulas in Practice (with Python)

To use a copula model, we typically follow these steps:

1. Select marginal distributions for each variable and fit their parameters to data.
2. Transform data to uniform ranks (e.g., using the empirical CDF for each variable).
3. Fit a copula to the transformed data (estimate copula parameters).
4. Use the copula to simulate new data or to calculate joint probabilities.

Let’s illustrate this with a simple Python example. We’ll simulate data from a known copula and then see if we can recover that dependence. Suppose \(X \sim \text{Beta}(2,5)\) and \(Y \sim \text{Beta}(5,2)\) (so \(X\) is skewed right, \(Y\) is skewed left, both supported on \([0,1]\)). We want them to have a moderate positive dependence. We’ll use a Gaussian copula with correlation \(\rho = 0.6\) to generate \((X, Y)\). Then we’ll pretend we just have \((X,Y)\) data and show how we’d estimate the copula correlation from it.

import numpy as np
from scipy.stats import norm, beta

np.random.seed(42)
n = 1000
rho = 0.6

# Step 1: Simulate latent correlated normals (U and V with correlation ~0.6)
u = np.random.normal(size=n)
v = np.random.normal(size=n)
v_correlated = rho * u + np.sqrt(1 - rho**2) * v  # induce correlation

# Step 2: Convert normals to uniforms via CDF (Phi)
U = norm.cdf(u)
V = norm.cdf(v_correlated)

# Step 3: Convert uniforms to desired marginals via inverse CDF (ppf)
X = beta(2, 5).ppf(U)
Y = beta(5, 2).ppf(V)

# Now, given X and Y (without knowing rho), estimate correlation via copula approach:
# Transform X, Y to uniforms (empirical CDF ranks)
rankX = (X.argsort().argsort() + 1) / (n + 1)  # this is a simple empirical CDF mapping
rankY = (Y.argsort().argsort() + 1) / (n + 1)
# Convert those uniforms to normal quantiles
normX = norm.ppf(rankX)
normY = norm.ppf(rankY)
# Compute correlation of the normal scores
estimated_rho = np.corrcoef(normX, normY)[0,1]

# Also compute naive Pearson correlation on X and Y directly
pearson_corr = np.corrcoef(X, Y)[0,1]
print(f"True latent correlation: {rho:.2f}")
print(f"Empirical Pearson correlation of X and Y: {pearson_corr:.2f}")
print(f"Estimated copula correlation from data: {estimated_rho:.2f}")

Expected output (approximately):

True latent correlation: 0.60  
Empirical Pearson correlation of X and Y: 0.54  
Estimated copula correlation from data: 0.57

We see that the naive Pearson correlation on \(X\) and \(Y\) (0.54) is a bit lower than the true correlation (0.60) because the marginals are non-linear (beta distributions). The copula correlation estimate (~0.57), which we got by transforming to normal scores, is closer to the true \(\rho\). In practice, one might use maximum likelihood to fit the copula parameter more rigorously, but this demonstrates the idea: by isolating the dependency via rank transforms, we can capture relationships that linear correlation on raw data might obscure.

To actually fit a copula model:

• We’d fit the marginals \(F_{X}, F_{Y}\) (in this example we knew them).
• Transform data to \((U_i, V_i)\) via \(u_i = F_X(x_i),\ v_i = F_Y(y_i)\).
• Choose a copula family (say Gaussian) and estimate the correlation (could use Kendall’s tau inversion or MLE).
• Now you have a full model: to simulate new pairs, sample \((u,v)\) from the fitted copula, then invert via
  \(x = F_X^{-1}(u),\quad y = F_Y^{-1}(v)\).

Real-world use case: Financial Risk Modeling

Perhaps the most famous (and infamous) application of copulas is in finance. For example:

• Portfolio Risk/Dependence: Assets (stocks, bonds, etc.) have individual behavior (marginal distributions) and correlations. A Gaussian copula might be used to model the joint distribution of returns. But if you worry about crashes, a t-copula or Clayton copula might better capture the chance of joint extreme losses.

• Credit Risk (CDOs): In the early 2000s, Gaussian copulas were heavily used to model the joint probability of loan defaults in a portfolio (to price CDO tranches). Each loan had a probability of default (marginal), and the Gaussian copula with some correlation structure “tied” them together. This gave a closed-form-ish way to compute risks of multiple defaults. However, as mentioned, the Gaussian copula can severely underestimate the probability of many simultaneous defaults if the correlation is modest. When housing market troubles hit broadly (something more like a tail event scenario), the model fell short. This contributed to mispricing of CDOs and has been cited as one cause of the 2008 crisis.

• Insurance: Copulas are used to model joint life insurance risks, operational risks, etc., where extreme events might be correlated (e.g., an earthquake causing many insurance payouts at once — that’s tail dependence among claims).

• Generative Modeling: Beyond finance, copulas are also a general tool for generating synthetic data. The Copula approach is used in some data science tools (like the Python sdv library) to learn a multivariate distribution from data and sample from it, by fitting marginals and a copula.

In practice, you might pick a copula by looking at data’s rank correlations and tail behavior. For example, if data shows that whenever one variable is high the other tends to also be high more than expected, a copula with upper tail dependence (like Gumbel) could be appropriate.

Using copulas in Python: There are libraries like copulas, statsmodels (which has some copula functions), and copulae. For instance, statsmodels.distributions.copula can sample from various copulas. Here’s a quick example of sampling from a Gumbel copula with parameter \(\theta = 2\):

from statsmodels.distributions.copula.api import GumbelCopula
copula = GumbelCopula(theta=2)
sample = copula.rvs(1000)  # 1000 samples of [U1, U2]

Now sample is a 1000x2 array of \(\text{Uniform}(0,1)\) pairs with Gumbel(2) dependence. We could then apply inverse CDFs to impose marginals.

To wrap up: Copulas let us mix-and-match marginal distributions with dependency structures. This modularity is incredibly useful. You could have one variable that’s Gaussian, another that’s exponential, and link them with a Clayton copula if you believe they crash together. Sklar’s theorem guarantees that as long as you have the marginals and a copula, you have a valid joint distribution.

However, caution is needed: choosing the wrong copula (dependence structure) can be as dangerous as choosing the wrong marginal distribution. Always check diagnostics like fitted vs empirical Kendall’s tau, tail dependencies, etc. Also, in high dimensions (\(d\) large), fitting copulas can become complex – vine copulas (pair-copula constructions) are one technique to build high-\(d\) copulas from bivariate ones.

We’ve now seen how copulas handle dependencies in space (between multiple variables). For our last topic, let’s look at modeling dependencies in time – specifically, how long until an event occurs – which brings us to Survival Analysis.

3. Survival Analysis: Time-to-Event Modeling

Not all prediction tasks are about “what” – sometimes it’s about “when”. Survival analysis (also called time-to-event analysis) is a branch of statistics that deals with analyzing the expected duration until one or more events happen. It originated in medical studies (hence “survival”: time until death), but it’s applied in engineering (time to component failure), finance (time to default), marketing (time to customer churn), and more. Survival analysis is crucial when we have data that is censored – i.e., for some subjects we don’t know the event time, only that it hasn’t happened yet as of the end of observation.

Formally, “Survival analysis is a branch of statistics for analyzing the expected duration of time until one event occurs, such as death in biological organisms or failure in mechanical systems.” In our context, the “event” could be a customer canceling a subscription (churn), a user returning to the app, a machine breaking down, etc. The time-to-event is a random variable \(T\) we want to model.

Why Not Treat it as Regression or Classification?

You might wonder, why not just use regression (predict time directly) or classification (predict if event happens by a certain time)? The reason is censoring and efficiency of using partial information. Censoring means for some subjects, the event has not occurred during the observation period, so we only know that \(T\) is greater than some value. For example, in a 6-month churn study, a user still active at 6 months is right-censored – we know they survived at least 6 months, but not their eventual churn time. Simply discarding them or treating them as non-churn can bias analyses.

In statistics, “censoring is a condition in which the value of an observation is only partially known.” Right-censoring (the most common type) occurs when we know lower bounds for \(T\). There’s also left-censoring (we only know an upper bound) and interval censoring (we know \(T\) lies in an interval). Survival analysis techniques are designed to include both exact event times and censored observations in a consistent likelihood framework, so no information is wasted.

The Survival Function and Kaplan-Meier Estimator

A fundamental concept is the survival function \(S(t) = P(T > t)\) – the probability an individual’s event time is later than time \(t\) (i.e., they “survive” beyond \(t\)). Often we also talk about the cumulative distribution \(F(t) = P(T \le t)\) (so \(F(t) = 1 - S(t)\)), or the density \(f(t)\). Another key function is the hazard function:

which is the instantaneous event rate at time \(t\) given survival until \(t\).

Kaplan-Meier Estimator: When we want to estimate the survival function from data (some observed event times, some censored times), the Kaplan-Meier (KM) estimator is the go-to non-parametric method. It’s also called the product-limit estimator. The idea is simple: you go through time from 0 upward, and whenever an event occurs, you drop the survival probability by a factor corresponding to that event, accounting for how many were “at risk” at that time. If some observations are censored (withdrawn) at time \(c\), they stop contributing to the risk set after \(c\).

The formula for the Kaplan-Meier estimator \(\hat{S}(t)\) is:

where \(t_1 < t_2 < \cdots\) are the distinct event times in the data, \(d_i\) is the number of events at time \(t_i\), and \(n_i\) is the number of individuals at risk just before time \(t_i\). Intuitively, for each event time, you multiply the survival probability by

This is equivalent to decrementing the survival curve in steps.

Properties: The KM estimator produces a stepwise survival curve that stays flat between event times and drops at events. It handles right-censoring: individuals who are censored at time \(c\) are counted in \(n_i\) up to time \(c\), then removed thereafter (they don’t count as at risk beyond their censoring point). If no censoring, KM essentially gives the empirical survival (proportion surviving past \(t\)). With censoring, it correctly accounts for the uncertainty – e.g., if half of participants are still alive at study end, the survival curve doesn’t drop them to 0 (like it would if you assumed they all died at end); instead, it will show survival leveling off with some people still “alive” at last follow-up.

Let’s see an example. We’ll simulate some survival data and compute the Kaplan-Meier curve:

import numpy as np
import matplotlib.pyplot as plt

# Simulate random survival times from an exponential distribution
np.random.seed(0)
n = 100
true_mean_time = 5.0
event_times = np.random.exponential(scale=true_mean_time, size=n)

# Impose a censoring time at 10 units
censor_time = 10
observed_times = np.minimum(event_times, censor_time)
event_occurred = (event_times <= censor_time).astype(int)  # 1 if event observed, 0 if censored

# Compute Kaplan-Meier estimate
times = np.sort(np.unique(observed_times))
surv_prob = []
at_risk = n
current_surv = 1.0
for t in times:
    d = np.sum((observed_times == t) & (event_occurred == 1))  # events at t
    c = np.sum((observed_times == t) & (event_occurred == 0))  # censored at t
    if d > 0:
        current_surv *= (1 - d / at_risk)
        surv_prob.append(current_surv)
    else:
        surv_prob.append(current_surv)
    at_risk -= (d + c)

# Plot the survival curve
plt.step([0] + list(times), [1] + surv_prob, where="post")
plt.xlabel("Time")
plt.ylabel("Survival probability")
plt.title("Kaplan-Meier Curve")
plt.ylim(0, 1.05)
plt.xlim(0, censor_time)
plt.show()

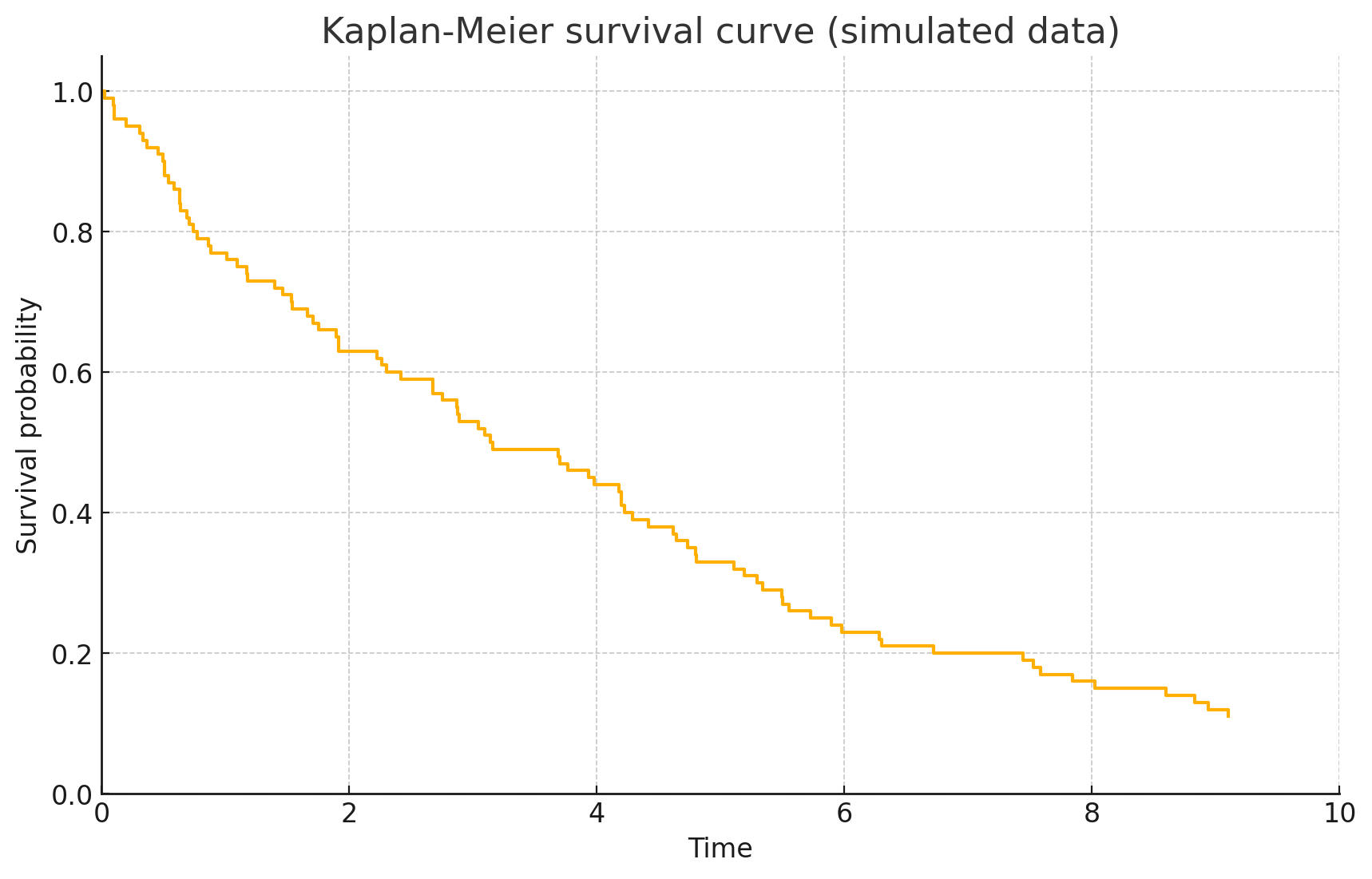
The curve starts at 1 (100% survival at time 0) and drops downwards as events occur. Notice it’s a step function: flat regions where no events happened, and drops at event times. If an individual is censored (e.g., lost to follow-up) at time 8, the curve does not drop (since no event), but the individual is simply removed from the risk set after 8 (reducing the denominator for later drops).

In our simulated data, by time 10, the survival probability is about 10–15%. We would interpret this as: there is approximately a 50% chance to survive \(\sim 4.5\) time units, a 20% chance to survive 6–7 units, etc., according to the curve.

The KM curve often has tick marks (vertical dashes) on it indicating censored observations (points where someone left the study without event). These ticks remind us that beyond that point, fewer subjects remain under observation. (In the above plot, we didn’t explicitly mark them, but one could add them.)

Kaplan-Meier is great for plotting and comparing survival between groups (e.g., using a log-rank test to see if two KM curves differ significantly). However, KM doesn’t directly tell us how features (covariates) affect survival. For that, we turn to regression models for survival data.

Cox Proportional Hazards Model

The Cox proportional hazards model (proposed by Sir David Cox in 1972) is the most commonly used survival regression model. It’s a semiparametric model: it makes no assumption about the baseline hazard function, but assumes that covariates have a multiplicative effect on the hazard.

The Cox model specifies that the hazard for an individual \(i\) at time \(t\) with covariate vector \(X_i = (x_{i1}, x_{i2}, \dots, x_{ip})\) is:

where \(h_0(t)\) is an unspecified baseline hazard function (the hazard when all \(x_{ij} = 0\)), and \(\beta_j\) are coefficients for each covariate. In vector form:

Interpretation: \(\exp(\beta_j)\) is the hazard ratio for a one-unit increase in covariate \(j\).

• If \(\beta_j = 0.5\), then that covariate being 1 unit higher multiplies the hazard by \(\exp(0.5) \approx 1.65\) (a 65% higher hazard, meaning the event is 1.65 times as likely at any given time, which also implies shorter expected survival time).
• If \(\beta_j = -0.7\), hazard is \(\exp(-0.7) \approx 0.50\) times (50%) for higher value – i.e., that covariate is protective, reducing the event rate.

Proportional Hazards assumption: The ratio of hazards for two individuals with covariates \(X_i\) and \(X_j\) is

which is constant over time (does not depend on \(t\)). That’s the “proportional” part – covariates shift the hazard up or down by a constant factor at all times. This may or may not hold true in all situations, but is a reasonable approximation in many cases (if not, there are extensions or one can include time-dependent covariate effects).

Fitting Cox models: Cox proposed a clever method using the partial likelihood – you can estimate the \(\beta\) coefficients without ever specifying \(h_0(t)\). Essentially, the partial likelihood considers, at each event time, the probability that the specific individual who had the event was the one to do so, given who was at risk at that time, and builds a likelihood from those comparisons.

Maximizing that yields \(\hat{\beta}\). The baseline hazard \(h_0(t)\) can then be estimated (once \(\beta\) is known) by non-parametric methods. So you get a full fitted model.

Most statistical packages (R’s survival package, Python’s lifelines or scikit-survival) can fit a Cox model readily. Output will give you:

• Coefficients and their significance
• Hazard ratios (\(\exp(\beta)\))
• Confidence intervals
• Survival curve estimates for given covariate profiles

The Cox model is powerful because it gives interpretable results and efficiently handles censoring, while not requiring strong assumptions on the time dependence of risk.

Example Use Case: Customer Churn – Let’s say we have a dataset of users with features like subscription_type (basic vs premium), avg_daily_minutes on the app, num_friend_connections, etc., and we track how long until they cancel their subscription (or if they haven’t yet by study end). A Cox model could be used to find which factors significantly affect churn hazard. For instance, we might find:

• Premium subscribers have \(\hat{\beta}_{\text{premium}} = -0.4\) → hazard ratio \(\approx \exp(-0.4) \approx 0.67\), meaning premium users churn at only 67% the rate of basic users (they stick around longer).
• Heavy daily usage might have \(\hat{\beta}_{\text{minutes}} = -0.01\) per minute of use → each additional minute reduces hazard by about 1% (makes churn slightly less likely).
• If num_friend_connections is high, perhaps hazard is lower (social connections keep users engaged).

From the fitted model, we could also predict survival curves for different profiles (e.g., a premium user with high activity vs a basic user with low activity) to see their estimated retention over time.

Cox vs Logistic: Note that if we dichotomized churn as churn/not by 6 months and ran logistic regression, we’d lose the nuance of when they churned and who was censored. Cox uses all the information:

• Someone who churned at 1 month contributes a lot of information (they had high hazard early).
• Someone who churned at 5 months contributes hazard info up to 5.
• Someone still active at 6 is contributing the fact that their hazard up to 6 was low enough that they survived (and they remain a censored observation beyond 6).

This makes use of ordering information and censoring, which logistic regression would ignore or treat incorrectly.

Extensions: Competing Risks and Beyond

Often there can be more than one type of event that “competes”. For example, in a study of time to heart attack, death by another cause is a competing risk – it censors the heart attack event but in a way that changes the probabilities. (Someone who dies from an accident can no longer have a heart attack, which affects the statistics differently than just being lost to follow-up.)

In customer analytics, we might consider:

• “Churn due to switching to a competitor” vs “churn due to lost interest” as two distinct events, or
• “Upgrade to higher plan” as an event that competes with “cancel service” – once they upgrade, the risk of cancel might change, or the original churn definition is no longer valid.

A competing risk is an event that precludes or changes the probability of the primary event of interest.

Standard survival analysis methods (like KM or Cox) that treat these competing events as non-informative censoring can give biased results, because the assumption of independent censoring is violated (the other event is informative).

To analyze competing risks, statisticians use:

• Cumulative incidence function (CIF): Instead of one survival curve, you estimate the probability of each type of event over time.
• Cause-specific hazards: Fit a separate Cox model for each event type, treating other types of events as censored, to see how covariates affect each specific hazard.
• Fine-Gray subdistribution hazards model: A model that directly works with the cumulative incidence. It estimates the effect of covariates on the subdistribution hazard, which differs from cause-specific hazard. The Fine-Gray model gives a hazard ratio that tells you the effect on the cumulative incidence of a specific event, in the presence of competing alternatives.

In less technical terms, for competing risks you answer questions like:
“By 1 year, what’s the probability of churn due to reason A vs reason B?”
This requires acknowledging that some users might churn due to A before they ever have a chance to churn due to B. In other words, the occurrence of one event type removes the subject from risk of the other, so the probabilities are interdependent.

For our purposes here, just be aware:
If multiple event types exist, special methods are needed. You cannot naively use a single survival curve or a single Cox model treating other events as ordinary censoring without checking if that’s appropriate.

Other extensions: There are many, including:

• Time-varying covariates: Cox models can handle covariates that change over time (e.g., a user’s behavior metrics recalculated each month) by slicing the data into intervals.

• Recurrent events: Some analyses deal with events that can happen repeatedly (e.g., hospital readmissions, reactivations, repeated purchases).

• Accelerated Failure Time (AFT) models: An alternative to Cox. AFT models assume a parametric form (like Weibull or log-normal) and model log event time as a linear function of covariates. It outputs time ratios instead of hazard ratios.

• Machine Learning survival models: Random survival forests, survival GBMs, and even deep learning models (e.g., DeepSurv, DeepHit) that incorporate survival loss functions. These methods can model nonlinearities and high-order interactions, though they often trade off interpretability.

Summing Up Survival Analysis (Use Case: User Retention Modeling)

To cement the ideas, here’s how you might apply survival analysis in user retention modeling:

• Define event and censoring:
  • Event = user churn (e.g., 30 days of inactivity or formal cancellation)
  • Censoring = user still active at end of observation period, or lost to follow-up
• Data structure:
  For each user, collect:
  • Start date
  • Churn date or last known active date
  • Covariates like usage patterns, demographics, app engagement metrics
• Exploratory analysis:
  • Plot Kaplan-Meier curve of user retention
  • Stratify curves by groups (e.g., referral vs organic sign-ups, free vs paid plans)
  • Estimate median survival time (e.g., “50% of users churn within 45 days”)
• Model building:
  • Fit a Cox proportional hazards model
  • Use (time, event) as the outcome
  • Include covariates like plan type, daily activity, friend count, app version
• Interpret results:
  • Identify which factors increase or decrease hazard
  • Example interpretations:
    • “Premium users have a 33% lower hazard”
    • “Users who added 5+ friends have 40% lower churn risk”
    • “Using the tutorial in the first session reduces churn risk by 25%”
• Check assumptions:
  • Use Schoenfeld residuals to test the proportional hazards assumption
  • If violated:
    • Add interaction terms with time
    • Use stratified Cox models
    • Consider time-varying covariates
• Apply the model:
  • Predict retention probabilities for different user personas
  • Flag high-risk users (e.g., top 10% in predicted hazard) for marketing interventions
  • Simulate lifetime value under different retention improvement strategies

Survival analysis provides far richer insight than simply computing average churn rate. It answers:

• When is churn happening?
• How fast is the population decaying?
• Which user types are more or less at risk?

It also uses partial data wisely – those censored users are still informative. In business terms, it sharpens your view of customer lifecycle dynamics and lets you target retention strategies with precision and clarity.

We’ve covered a lot of ground:

• Probabilistic Graphical Models: Using graphs to encode complex joint probability models. We saw how Bayesian Networks factorize distributions and enable reasoning (medical diagnosis example), and how Conditional Random Fields handle sequential labeling problems in NLP by accounting for neighbor relationships. We discussed inference challenges and methods in PGMs.
• Copulas: A method to construct flexible multivariate distributions by pairing any marginals with a chosen dependency structure. We learned about Sklar’s theorem, Gaussian vs heavy-tailed copulas, and even saw how to fit a copula parameter from data. The financial risk case study illustrated why copulas matter when modeling correlated extreme events.
• Survival Analysis: Techniques for time-to-event data. We explained censoring, estimated survival curves via Kaplan-Meier, introduced the Cox proportional hazards model to assess covariate effects on survival (with a churn analysis lens), and noted extensions like competing risks.

Despite the technical depth, the unifying theme is probabilistic thinking. All these methods are grounded in probability theory, providing a coherent way to handle uncertainty and variability:

• PGMs let us articulate what we know (or assume) about dependencies qualitatively (via a graph) and quantitatively (via probabilities), then compute implications.
• Copulas let us break a hard multivariate problem into easier pieces (one-dimensional margins and a copula for dependency).
• Survival analysis acknowledges that when something happens is as important as whether it happens, and gives tools to model that, even with incomplete data.

For an early-stage data scientist or student, mastering these topics unlocks a new level of modeling sophistication. You’ll be equipped to:

• Build models that mirror real-world structures (e.g. causal chains, feedback loops) rather than treating everything as an IID spreadsheet.
• Better capture the behavior of multiple related variables, especially in non-normal data.
• Analyze longitudinal outcomes and durations, which are ubiquitous in domains from healthcare to customer analytics, with appropriate statistical rigor.

Each topic we discussed has a rich literature and many more nuances:

• PGMs lead into Bayesian inference, causal discovery, deep generative models, etc.
• Copulas open up into high-dimensional dependence modeling, vine copulas, extreme value theory.
• Survival analysis connects to reliability engineering, epidemiology (e.g. competing risks in clinical trials), and modern machine learning survival methods.

Encourage you to dig deeper into any of these that pique your interest. Try applying a Bayesian network to a toy problem (there are libraries like pgmpy), or use lifelines in Python to analyze some churn data with Kaplan-Meier and Cox models. And next time you face a modeling problem, think about whether these advanced probabilistic tools can give you an edge in insight or performance. Happy modeling!