Data Preprocessing Part 6: Dimensionality Reduction

1. Introduction
2. Theoretical Foundations
3. Linear Dimensionality Reduction Techniques
4. Non-Linear Dimensionality Reduction Techniques
5. Feature Selection as Dimensionality Reduction
- 5.1 L0-Based Feature Selection
- 5.2 Other Feature Selection Methods
6. Other Dimensionality Reduction Techniques
7. Practical Considerations
8. Challenges and Pitfalls
9. Best Practices and Guidelines
Wrapping Up

Picture this.

You’re in a grand room—no walls, just mirrors. Everywhere you look, you see reflections—of yourself, of the lights, of fragments of images that bounce endlessly, distorting space. You take one step forward, and your reflection shatters into hundreds. Orientation becomes meaningless. Every direction looks plausible. Every step feels confusing. This, dear reader, is what your algorithm feels like when working with high-dimensional data.

Back in 2008, a group of biologists were working on classifying cancer types using gene expression data. Each patient’s genome was a data point—tens of thousands of gene expressions but only a few hundred patients. The dataset was massive in width but shallow in depth. Every machine learning model they threw at it failed—overfitting, underperforming, or simply stalling. It wasn’t that the models were bad. The data was just too vast in its dimensional sprawl, too noisy, too sparse.

Then came the twist. One data scientist quietly applied Principal Component Analysis (PCA), reducing the number of features from 20,000 to just 50—carefully chosen to retain maximum variance. Suddenly, everything clicked. The classifier began separating cancer types with remarkable accuracy. Not because the model changed. But because the data finally made sense.

Welcome to the world of Dimensionality Reduction—where less is often more, and simplicity is a gateway to clarity.

As machine learning practitioners, we’re often obsessed with collecting more features, more attributes, more signals. But high-dimensional data carries a hidden curse: it dilutes patterns, amplifies noise, and makes computation brittle. Without dimensionality reduction, we risk feeding our models data that is uninformative or even misleading.

Whether it’s compressing image data, visualizing multi-feature clustering, preprocessing for unsupervised learning, or eliminating irrelevant features in a genomic study—dimensionality reduction acts as the unsung hero of preprocessing pipelines.

And that’s what this final chapter of our Data Preprocessing series is all about.

We’ll journey through linear techniques like PCA, SVD, and LDA, then traverse into the rich terrain of non-linear methods like t-SNE, UMAP, and autoencoders. We’ll also explore feature selection, clustering-based reductions, and niche methods like Isomap, LLE, and feature agglomeration—each with Python examples and real-world case studies.

This isn’t just about shrinking data. It’s about sculpting it—carving away the extraneous until what remains is beautiful, learnable, and useful.

Let’s begin.

1. Introduction

1.1 Definition and Importance

Dimensionality reduction refers to the process of reducing the number of input variables (features) in a dataset while retaining as much meaningful information as possible. It’s not just about shrinking the size of the data—it’s about uncovering latent patterns, simplifying models, and improving generalization. In the age of big data, where datasets often include hundreds or thousands of features, dimensionality reduction becomes essential for maintaining model interpretability and efficiency.

Well-known techniques like Principal Component Analysis (PCA) and t-SNE are frequently used to reduce the feature space before applying downstream machine learning models or for visualization. These methods help address the problems posed by high-dimensional data and offer ways to compress, visualize, and extract meaningful structure from it.

1.2 The Curse of Dimensionality

The “curse of dimensionality” is a term coined to describe the exponential increase in complexity and sparsity that arises when working with high-dimensional data. As the number of features grows, the volume of the space increases so rapidly that data points become sparse and distances between them become less meaningful. This affects:

Model performance: Increased risk of overfitting due to too many irrelevant or redundant features.
Computational cost: Memory and time complexity grow significantly with dimensionality.
Distance-based algorithms: Techniques like k-NN and clustering rely on meaningful distance metrics, which break down in high dimensions.

These challenges necessitate reducing the dimensions to something more tractable and meaningful.

1.3 Goals of Dimensionality Reduction

The key objectives behind dimensionality reduction include:

Reducing noise: Strip away uninformative or redundant features to clarify signal.
Improving model performance: Less complex models generalize better and overfit less.
Enabling visualization: High-dimensional data can be projected into 2D or 3D for exploration and insight.
Decreasing computational load: Fewer features reduce time and memory usage in both training and inference stages.

1.4 Applications of Dimensionality Reduction

Dimensionality reduction is widely used across domains:

Data Compression: Reduce storage needs in image processing, genomics, etc.
Visualization: Techniques like PCA, t-SNE, and UMAP make it easier to explore high-dimensional datasets.
Feature Engineering: Transform high-dimensional raw features into lower-dimensional meaningful representations.
Noise Reduction: Remove irrelevant or redundant features from datasets before modeling.
Preprocessing for Machine Learning: Boost training speed and performance for downstream models.

2. Theoretical Foundations

Dimensionality reduction techniques are not black-box tools—they are mathematical constructs grounded in linear algebra, geometry, and statistics. Understanding the theory behind them not only empowers us to use them effectively but also reveals the elegant assumptions and trade-offs that make them work. This section lays the groundwork for both linear and non-linear dimensionality reduction by unpacking the key mathematical ideas that support them.

2.1 Linear Algebra Basics

At the heart of dimensionality reduction lies the concept of linear transformation—projecting data from a high-dimensional space to a lower-dimensional one while retaining its essential structure. Let’s unpack the key building blocks.

Covariance Matrix

The covariance matrix captures linear relationships between features. Given mean-centered data matrix \(X\):

\[\Sigma = \frac{1}{n-1} X^\top X \in \mathbb{R}^{d \times d}\]

Each entry \(\Sigma_{ij}\) represents the covariance between feature \(i\) and feature \(j\). This matrix is symmetric and positive semi-definite, and plays a central role in PCA.

Eigen Decomposition

The eigen decomposition of a symmetric matrix like \(\Sigma\) yields eigenvectors and eigenvalues:

\[\Sigma v_i = \lambda_i v_i\]

where:

\(v_i\) is an eigenvector,
\(\lambda_i\) is the corresponding eigenvalue.

The eigenvectors form an orthonormal basis, and each eigenvalue indicates the variance explained along that direction. PCA uses these eigenvectors (called principal components) to project data into directions of maximal variance.

Singular Value Decomposition (SVD)

For arbitrary data matrices, the SVD is more general than eigen decomposition. Any matrix \(X \in \mathbb{R}^{n \times d}\) can be factorized as:

\[X = U \Sigma V^\top\]

where:

\(U \in \mathbb{R}^{n \times n}\) contains the left singular vectors,
\(\Sigma \in \mathbb{R}^{n \times d}\) is a diagonal matrix with non-negative singular values \(\sigma_1 \ge \sigma_2 \ge \dots \ge 0\),
\(V \in \mathbb{R}^{d \times d}\) contains the right singular vectors (orthonormal columns).

Truncated SVD retains only the top \(k\) singular values and vectors:

\[X_k = U_k \Sigma_k V_k^\top\]

This is the optimal low-rank approximation of \(X\) in Frobenius norm.

2.2 Manifold Learning

Not all data lies on a flat Euclidean subspace. Real-world data often lies on a manifold—a smooth, non-linear surface embedded in a high-dimensional space. The key idea of manifold learning is that while the ambient space may be \(\mathbb{R}^d\), the intrinsic dimensionality of the data is much lower (say, \(\mathbb{R}^k\), where \(k \ll d\)).

For example, imagine images of a rotating object under constant lighting. Though each image is represented by thousands of pixels (dimensions), the underlying variation may be governed by just a few variables: rotation angle and viewpoint.

Manifold learning techniques (like Isomap, LLE, UMAP) aim to preserve local neighborhoods or geodesic distances to uncover this lower-dimensional structure.

2.3 Distance Metrics in High Dimensions

Dimensionality reduction methods often depend on measuring similarity between data points. The choice of distance metric is foundational to algorithms like k-NN, t-SNE, UMAP, and even PCA when analyzing variance.

Euclidean Distance

The straight-line distance in Euclidean space:

\[d(x, y) = \sqrt{\sum_{i=1}^d (x_i - y_i)^2}\]

This works well when all features are equally scaled and data is dense.

Manhattan Distance

The \(L_1\) norm (taxicab metric):

\[d(x, y) = \sum_{i=1}^d |x_i - y_i|\]

Less sensitive to outliers than Euclidean distance.

Cosine Similarity

Often used in text mining and recommendation systems:

\[\text{cosine}(x, y) = \frac{x \cdot y}{\|x\| \|y\|}\]

This measures the angle between two vectors and is scale-invariant.

Curse of Dimensionality

As dimensionality increases:

Distances between points converge (relative distances lose meaning).
Most points become nearly equidistant.
Sparsity increases, making generalization difficult.

This is known as the curse of dimensionality, which makes reducing the feature space not just desirable but necessary for robust learning.

2.4 Variance and Information Retention

When reducing dimensions, we want to preserve maximum information. In PCA, this is done by keeping components with the largest eigenvalues—those that retain the most variance.

Explained Variance

Let \(\lambda_1, \lambda_2, \dots, \lambda_d\) be the eigenvalues from the covariance matrix. The explained variance ratio for the top \(k\) components is:

\[\text{EVR}(k) = \frac{\sum_{i=1}^k \lambda_i}{\sum_{j=1}^d \lambda_j}\]

This ratio helps decide the number of components to keep (e.g., retain 95% of variance).

Bias–Variance Trade-off

Reducing dimensions simplifies the model (reduces variance) but may omit relevant information (introduces bias). A balanced reduction improves generalization:

Too many components: overfitting
Too few components: underfitting

This trade-off underlies many choices in both supervised and unsupervised learning.

By mastering these foundational concepts, we are now equipped to explore specific dimensionality reduction techniques with mathematical rigor and practical intuition.

3. Linear Dimensionality Reduction Techniques

Linear dimensionality reduction methods aim to find linear projections of the data that capture most of the variation. These techniques assume the data lies near a linear subspace of the original high-dimensional space. Among them, the most widely used and foundational method is Principal Component Analysis (PCA).

3.1 Principal Component Analysis (PCA)

PCA is the go-to algorithm for dimensionality reduction when data is numeric, continuous, and linearly correlated. It transforms the data into a new coordinate system such that the greatest variance lies on the first axis (principal component), the second greatest on the second axis, and so on.

Core Concepts

Eigen Decomposition of the Covariance Matrix

Let \(X \in \mathbb{R}^{n \times d}\) be a dataset with \(n\) samples and \(d\) features, and assume it is mean-centered. The sample covariance matrix is:

\[\Sigma = \frac{1}{n - 1} X^\top X\]

We perform eigen decomposition:

\[\Sigma v_i = \lambda_i v_i\]

\(v_i\) are the eigenvectors (principal directions).
\(\lambda_i\) are the eigenvalues, representing variance captured along each direction.

The eigenvectors provide a new basis, and projecting the data onto the top \(k\) eigenvectors gives the principal components.

Projection and Variance

The projection of a data point \(x\) onto the \(i^\text{th}\) principal component \(v_i\) is:

\[z_i = x^\top v_i\]

Stacking the top \(k\) eigenvectors into a matrix \(V_k\), the reduced data is:

\[Z = X V_k \in \mathbb{R}^{n \times k}\]

This projection maximizes the retained variance under the constraint of linearity and orthogonality.

Step-by-Step Process

Let’s walk through PCA mathematically and then implement it in Python.

Step 1: Standardize the Data

PCA is sensitive to the scale of features, so we begin by standardizing:

\[x_j' = \frac{x_j - \mu_j}{\sigma_j}\]

where \(\mu_j\) and \(\sigma_j\) are the mean and standard deviation of feature \(j\).

Step 2: Compute Covariance Matrix

Calculate:

\[\Sigma = \frac{1}{n - 1} X^\top X\]

Step 3: Eigen Decomposition

Solve:

\[\Sigma v_i = \lambda_i v_i\]

Sort \(\lambda_i\) in descending order and pick the top \(k\).

Step 4: Project Data

Transform the original dataset:

\[Z = X V_k\]

Applications

PCA is widely used in:

Genomics: Reducing gene expression matrices from 20,000+ features to a handful of informative axes.
Image Processing: Compressing images by projecting pixel intensities onto top principal components.
Denoising: Low-variance components often contain noise; removing them improves data quality.

Limitations

Linearity Assumption: PCA only captures linear correlations.
Sensitivity to Outliers: Outliers can distort the principal directions.
Interpretability: The new axes (principal components) are linear combinations, often hard to interpret directly.

Python Implementation

Let’s apply PCA to the famous Iris dataset and visualize the explained variance.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.decomposition import PCA
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_iris

# Load data
iris = load_iris()
X = pd.DataFrame(iris.data, columns=iris.feature_names)

# Standardize
scaler = StandardScaler()
X_std = scaler.fit_transform(X)

# PCA
pca = PCA()
X_pca = pca.fit_transform(X_std)

# Scree plot (Explained Variance)
explained_variance = pca.explained_variance_ratio_
cum_var = np.cumsum(explained_variance)

plt.figure(figsize=(8, 5))
plt.plot(range(1, len(cum_var)+1), cum_var, marker='o')
plt.xlabel('Number of Principal Components')
plt.ylabel('Cumulative Explained Variance')
plt.title('Scree Plot')
plt.grid(True)
plt.show()

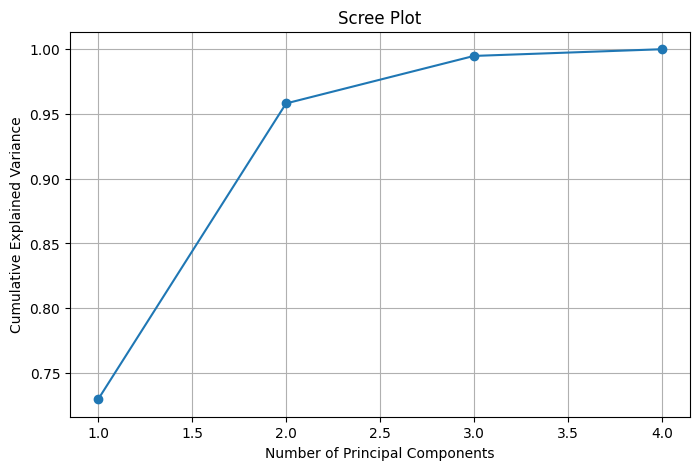
One of the most intuitive tools in PCA is the scree plot—a graphical representation of the eigenvalues (explained variance) associated with each principal component. On the x-axis, we plot the component number (1, 2, 3, …), and on the y-axis, the corresponding proportion of variance explained. The shape of this curve helps determine how many components are worth keeping.

The critical insight from a scree plot lies in identifying the “elbow point”—the point after which adding more components yields diminishing returns in explained variance. This is where the curve starts to flatten out. For example, if the first 2 or 3 components explain 90–95% of the variance, and subsequent components add only marginal gains, it’s often optimal to retain just those initial components.

By selecting the number of principal components based on the scree plot, we achieve a balanced trade-off between dimensionality reduction and information retention—simplifying the dataset while preserving its essential structure. This plot is particularly helpful when no domain-specific heuristic is available to choose the dimensionality ahead of time.

This scree plot helps determine the optimal \(k\) such that:

\[\sum_{i=1}^k \lambda_i \bigg/ \sum_{j=1}^d \lambda_j \geq \text{Threshold}\]

Often, a threshold of 95% is used.

Variants of PCA

Incremental PCA

Processes data in mini-batches, suitable for large datasets that don’t fit in memory.

from sklearn.decomposition import IncrementalPCA

ipca = IncrementalPCA(n_components=2, batch_size=10)
X_ipca = ipca.fit_transform(X_std)

Kernel PCA

Projects data into a non-linear feature space using kernels (RBF, polynomial, sigmoid), allowing non-linear structure to emerge.

from sklearn.decomposition import KernelPCA

kpca = KernelPCA(n_components=2, kernel='rbf', gamma=15)
X_kpca = kpca.fit_transform(X_std)

By transforming complex, high-dimensional data into structured, informative low-dimensional representations, PCA enables both interpretability and performance. However, its assumptions should be carefully matched to the problem. In the next section, we’ll see how Truncated SVD handles sparse data efficiently, especially in text mining.

3.2 Truncated Singular Value Decomposition (SVD)

While PCA is built on the eigen decomposition of the covariance matrix, Truncated Singular Value Decomposition (SVD) offers a more memory-efficient and computationally scalable alternative—especially valuable when dealing with sparse, high-dimensional datasets, such as those in natural language processing or collaborative filtering tasks.

Core Concepts

Let \(X \in \mathbb{R}^{n \times d}\) be a data matrix, possibly sparse and not necessarily mean-centered. The full SVD of this matrix decomposes it as:

\[X = U \Sigma V^\top\]

where:

\(U \in \mathbb{R}^{n \times r}\) contains the left singular vectors (orthonormal),
\(\Sigma \in \mathbb{R}^{r \times r}\) is a diagonal matrix of singular values \(\sigma_1 \ge \sigma_2 \ge \cdots \ge \sigma_r > 0\),
\(V^\top \in \mathbb{R}^{r \times d}\) contains the right singular vectors,
and \(r = \text{rank}(X)\).

The key to dimensionality reduction lies in truncating this decomposition—retaining only the top \(k\) singular values and their corresponding vectors:

\[X_k = U_k \Sigma_k V_k^\top\]

This produces the best low-rank approximation of \(X\) in terms of the Frobenius norm:

\[\|X - X_k\|_F = \min_{\text{rank}(A) = k} \|X - A\|_F\]

PCA vs. Truncated SVD

While PCA also uses an SVD internally, it first centers the data and works on the covariance matrix. In contrast, Truncated SVD operates directly on the raw matrix—without requiring centering or forming a covariance matrix—making it ideal for sparse data (e.g., TF-IDF matrices in NLP). Hence, it’s often used in Latent Semantic Analysis (LSA).

Applications

Truncated SVD is widely applied in:

Text Mining / NLP:
- Used in Latent Semantic Analysis (LSA) to reduce large term-document matrices (e.g., TF-IDF) to latent semantic dimensions.
- Captures word co-occurrence and topic-like structures in an unsupervised fashion.
Recommender Systems:
- Reduces user-item interaction matrices into latent factors.
- Basis for matrix factorization methods in collaborative filtering.

Python Implementation on Sparse Text Data

Let’s perform Truncated SVD on a sparse TF-IDF matrix derived from a small text corpus.

from sklearn.decomposition import TruncatedSVD
from sklearn.feature_extraction.text import TfidfVectorizer

# Sample corpus
corpus = [
    "Data science is fun",
    "Machine learning is a part of data science",
    "Deep learning is a branch of machine learning",
    "I love learning new things",
    "Science and data go hand in hand"
]

# Create sparse TF-IDF matrix
vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(corpus)

# Apply Truncated SVD (LSA)
svd = TruncatedSVD(n_components=2)
X_reduced = svd.fit_transform(X)

print("Explained variance ratio:", svd.explained_variance_ratio_)
print("Reduced data shape:", X_reduced.shape)

This code:

Converts text into a sparse TF-IDF matrix.
Applies Truncated SVD to extract the top 2 latent dimensions.
Outputs the explained variance and reduced representation.

You can visualize the 2D embedding or use it for downstream clustering, classification, or semantic analysis.

Advantages

Efficiency: Works directly on sparse matrices without centering—saves memory and computation.
Scalability: Suitable for large-scale applications like recommender systems and web-scale NLP.
Interpretability of singular values: Provides insight into dimensionality and variance concentration.

Limitations

Component Interpretability: Unlike PCA, the singular vectors in Truncated SVD are not directly aligned with variance-maximizing directions, making component interpretation more abstract.
Not Centered: Since it does not center the data, it may retain bias if centering is important to the application.
Linear: Like PCA, it only captures linear relationships.

In short, Truncated SVD extends the power of linear dimensionality reduction to sparse and massive datasets—unlocking applications that standard PCA simply cannot scale to. In the next section, we’ll explore Linear Discriminant Analysis (LDA), a supervised technique that maximizes class separability instead of variance.

3.3 Linear Discriminant Analysis (LDA)

Unlike PCA or Truncated SVD, which are unsupervised and optimize for variance, Linear Discriminant Analysis (LDA) is a supervised dimensionality reduction technique. It explicitly takes class labels into account and seeks a transformation that maximizes class separability. As such, LDA is widely used in classification pipelines, especially when interpretability and discriminative power are priorities.

Core Concepts

Let’s suppose we have a dataset with \(n\) samples, each belonging to one of \(C\) classes. LDA finds a projection of the data onto a lower-dimensional subspace such that:

Between-class variance is maximized.
Within-class variance is minimized.

The goal is to solve the generalized eigenvalue problem based on two scatter matrices:

Within-class scatter matrix:
\[S_W = \sum_{c=1}^{C} \sum_{x_i \in \mathcal{D}_c} (x_i - \mu_c)(x_i - \mu_c)^\top\]
where \(\mu_c\) is the mean vector of class \(c\), and \(\mathcal{D}_c\) is the set of all samples in class \(c\).
Between-class scatter matrix:
\[S_B = \sum_{c=1}^{C} n_c (\mu_c - \mu)(\mu_c - \mu)^\top\]
where \(\mu\) is the global mean of all samples, and \(n_c\) is the number of samples in class \(c\).

The optimization objective of LDA is to find a projection matrix \(W\) that maximizes:

\[J(W) = \frac{|W^\top S_B W|}{|W^\top S_W W|}\]

Solving this gives us the directions that best separate the class means while minimizing variance within each class.

Intuition

Think of LDA as a way to “untangle” overlapping classes in the feature space. While PCA aligns projections along directions of greatest overall variance (which might be noisy or class-agnostic), LDA deliberately aligns them along axes where class centers are maximally distant and clusters are tight.

The maximum number of useful LDA components is at most \(C - 1\), where \(C\) is the number of classes.

Applications

Face Recognition: LDA (often combined with PCA) has been widely used in algorithms like Fisherfaces, where it reduces facial images into a discriminative subspace.
Bioinformatics: LDA is employed to reduce genomic data dimensions before classification (e.g., disease prediction).
Text Classification: Applied to topic-based document classification where class labels are available.

Python Implementation on a Classification Task

Let’s apply LDA to the Iris dataset—using the class labels to find a lower-dimensional space that separates flower species.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.preprocessing import StandardScaler

# Load data
iris = load_iris()
X = iris.data
y = iris.target
target_names = iris.target_names

# Standardize features
scaler = StandardScaler()
X_std = scaler.fit_transform(X)

# Apply LDA
lda = LinearDiscriminantAnalysis(n_components=2)
X_lda = lda.fit_transform(X_std, y)

# Plot
plt.figure(figsize=(8, 5))
for i, label in enumerate(np.unique(y)):
    plt.scatter(X_lda[y == label, 0], X_lda[y == label, 1], label=target_names[label])
plt.xlabel("LD1")
plt.ylabel("LD2")
plt.title("LDA: Iris Dataset Projection")
plt.legend()
plt.grid(True)
plt.show()

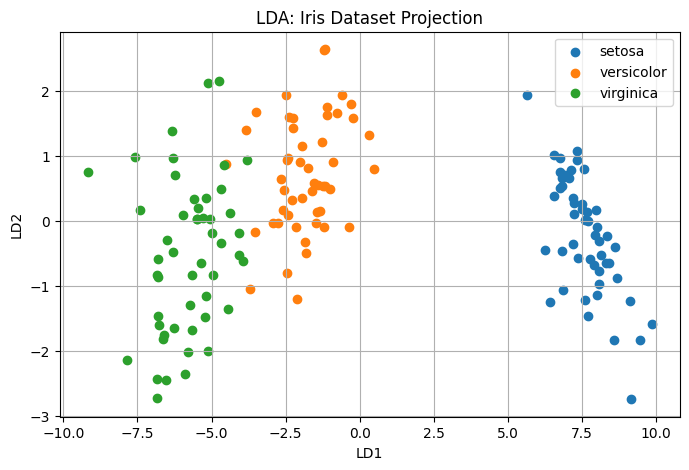
This code standardizes the dataset, applies LDA to project it into a 2D space, and visualizes the result. You’ll notice that LDA creates tight, well-separated clusters for each class, far more explicitly than PCA would.

Limitations

Distributional Assumption: LDA assumes that each class follows a Gaussian distribution with identical covariance matrices (homoscedasticity). This assumption is often violated in real-world data.
Linearity: Like PCA, LDA assumes that the optimal class boundaries are linearly separable.
Overfitting in Small Samples: If the number of features is large compared to the number of samples, LDA may overfit or become numerically unstable (especially with singular \(S_W\)).

In summary, Linear Discriminant Analysis serves as a powerful technique when labels are available and class discrimination is the end goal. It complements PCA by adding supervised signal into the projection process, and when used correctly, can significantly boost the interpretability and performance of classification tasks—especially in low-sample, high-dimensional regimes.

In the next section, we move beyond linearity and into the non-linear world with techniques like t-SNE, UMAP, and Autoencoders, which uncover manifold structures that linear methods cannot.

4. Non-Linear Dimensionality Reduction Techniques

Linear methods like PCA or LDA assume that data lies near a linear subspace. However, many real-world datasets (e.g., images, text, genomics) lie on non-linear manifolds embedded within high-dimensional space. Non-linear dimensionality reduction techniques aim to uncover these intrinsic structures.

Among the most popular of these is t-Distributed Stochastic Neighbor Embedding (t-SNE), a tool that excels in visualizing high-dimensional data in 2D or 3D.

4.1 t-Distributed Stochastic Neighbor Embedding (t-SNE)

Core Concepts

t-SNE is a probabilistic, non-linear algorithm that maps high-dimensional data to a lower-dimensional space while preserving local neighborhood structure. It is not meant for general modeling or compression, but rather for exploration and visualization of patterns like clusters or manifolds.

At its heart, t-SNE tries to match the similarity between data points in high dimensions and their similarity in low dimensions.

Mathematical Intuition

In high-dimensional space, for each point \(x_i\), we compute pairwise similarities with other points using a Gaussian kernel:

\[p_{j|i} = \frac{\exp(-\|x_i - x_j\|^2 / 2 \sigma_i^2)}{\sum_{k \neq i} \exp(-\|x_i - x_k\|^2 / 2 \sigma_i^2)}\]

Then symmetrize:

\[p_{ij} = \frac{p_{j|i} + p_{i|j}}{2n}\]

These define the high-dimensional joint probabilities. In the low-dimensional map (say, 2D), we place points \(y_i\) and define similar probabilities using a Student’s t-distribution with 1 degree of freedom:

\[q_{ij} = \frac{(1 + \|y_i - y_j\|^2)^{-1}}{\sum_{k \neq l} (1 + \|y_k - y_l\|^2)^{-1}}\]

t-SNE minimizes the Kullback-Leibler divergence between the two distributions:

\[KL(P \| Q) = \sum_{i \neq j} p_{ij} \log \left( \frac{p_{ij}}{q_{ij}} \right)\]

This encourages nearby points to remain close in the low-dimensional space, creating a visually meaningful embedding.

Perplexity and Its Impact

A key hyperparameter in t-SNE is perplexity, which controls the balance between local and global aspects of the data. It is related to the effective number of neighbors considered for each point:

Low perplexity (5–30): Focuses on very local structure.
High perplexity (50+): Preserves more global relationships but may lose tight clustering.

There is no one-size-fits-all; experimentation is essential.

Applications

t-SNE is widely used for data visualization in:

Natural Language Processing: Visualizing word embeddings like Word2Vec or GloVe.
Genomics: Visualizing single-cell RNA-seq data clusters.
Image Analysis: Understanding CNN-encoded features or unsupervised clusters.
Anomaly Detection: Visualizing latent structures in security logs, customer behavior, etc.

Python Implementation

Here’s a working example using scikit-learn on the Iris dataset:

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.manifold import TSNE
from sklearn.preprocessing import StandardScaler

# Load and standardize data
iris = load_iris()
X = StandardScaler().fit_transform(iris.data)
y = iris.target
target_names = iris.target_names

# Apply t-SNE with tuning
tsne = TSNE(n_components=2, perplexity=30, n_iter=1000, random_state=42)
X_tsne = tsne.fit_transform(X)

# Plot
plt.figure(figsize=(8, 6))
for label in np.unique(y):
    plt.scatter(X_tsne[y == label, 0], X_tsne[y == label, 1], label=target_names[label])
plt.xlabel("t-SNE 1")
plt.ylabel("t-SNE 2")
plt.title("t-SNE Visualization of Iris Dataset")
plt.legend()
plt.grid(True)
plt.show()

This code runs t-SNE with perplexity = 30 and maps the 4D Iris dataset to a 2D space. The result is often more cluster-revealing than PCA or LDA.

Limitations

While t-SNE is powerful for visualization, it comes with some critical caveats:

No Inverse Transform: You can’t map reduced points back to original space.
Not for Feature Engineering: The components are not meaningful for modeling.
Computational Cost: Quadratic in time complexity with respect to number of samples.
Non-Deterministic: Results can vary unless random_state is fixed.

Best Practices

Always scale your data before using t-SNE.
Use only for visualization, not for building ML models.
Experiment with perplexity values (5–50) to capture structure at the right scale.
Run multiple times and average interpretations—t-SNE is stochastic.

t-SNE is a brilliant lens through which to see your data—not analyze or model it, but explore its structure. When used correctly, it can reveal hidden clusters, separability, and latent manifolds that other techniques simply blur. Up next, we dive into UMAP, a manifold-learning algorithm that attempts to preserve both local and global structure—with far more scalability.

4.2 Uniform Manifold Approximation and Projection (UMAP)

As powerful as t-SNE is, it has its limitations—most notably, it discards global structure, scales poorly with large datasets, and lacks interpretability. Enter UMAP: a non-linear dimensionality reduction technique based on rigorous mathematical foundations from topological data analysis. UMAP is designed to preserve both local neighborhoods and global relationships, while offering faster runtimes and better scalability.

Core Concepts

UMAP builds on manifold learning theory and algebraic topology—specifically:

Fuzzy simplicial sets: Used to construct a graphical representation of local neighborhoods.
Manifold approximation: Embeds this graph into lower dimensions while preserving its structure.

Let’s break it down.

Mathematical Foundations

Given a high-dimensional dataset \(X = \{x_1, x_2, \dots, x_n\}\), UMAP starts by constructing a weighted k-nearest neighbor graph using:

Distance metric: Usually Euclidean, but others (e.g., cosine) can be used.
Local connectivity: Each point’s neighborhood is converted into a fuzzy set with connection strengths based on distance.

Formally, for each point \(x_i\) and its neighbors \(x_j\), UMAP defines a probability of connection:

\[p_{ij} = \exp\left( -\frac{d(x_i, x_j) - \rho_i}{\sigma_i} \right)\]

Where:

\(\rho_i\) ensures that nearest neighbor distances are non-zero.
\(\sigma_i\) is determined by solving for a smooth fuzzy connectivity.

In the low-dimensional space, a similar probability \(q_{ij}\) is defined, and UMAP minimizes the cross-entropy between the two fuzzy simplicial sets:

\[C = \sum_{i \neq j} \left[ p_{ij} \log q_{ij} + (1 - p_{ij}) \log(1 - q_{ij}) \right]\]

This encourages the structure of neighborhoods in high-D space to be preserved in the low-D embedding.

Local and Global Structure

Unlike t-SNE, which focuses heavily on local structure (small clusters), UMAP strikes a balance:

Local fidelity: Maintains meaningful neighborhoods.
Global cohesion: Retains the relative positioning of distant clusters.

This makes UMAP particularly powerful for cluster-preserving visualizations that also give a sense of how clusters relate to each other.

Applications

UMAP has rapidly gained popularity for:

Clustering and Preprocessing:
- Compressing data before applying k-means, DBSCAN, or hierarchical clustering.
Visualization of Word Embeddings, Single-cell Genomics, Images:
- Preserves separability and structure.
Accelerating ML Pipelines:
- Used to reduce feature space for faster downstream training.

Python Implementation

Here’s a comparison of UMAP and t-SNE on the Iris dataset:

import matplotlib.pyplot as plt
import numpy as np
import umap
from sklearn.datasets import load_iris
from sklearn.preprocessing import StandardScaler
from sklearn.manifold import TSNE

# Load and scale data
iris = load_iris()
X = StandardScaler().fit_transform(iris.data)
y = iris.target
target_names = iris.target_names

# UMAP
umap_model = umap.UMAP(n_neighbors=15, min_dist=0.1, random_state=42)
X_umap = umap_model.fit_transform(X)

# t-SNE for comparison
tsne = TSNE(n_components=2, perplexity=30, random_state=42)
X_tsne = tsne.fit_transform(X)

# Plot UMAP
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
for label in np.unique(y):
    plt.scatter(X_umap[y == label, 0], X_umap[y == label, 1], label=target_names[label])
plt.title("UMAP Projection")
plt.xlabel("UMAP 1")
plt.ylabel("UMAP 2")
plt.legend()
plt.grid(True)

# Plot t-SNE
plt.subplot(1, 2, 2)
for label in np.unique(y):
    plt.scatter(X_tsne[y == label, 0], X_tsne[y == label, 1], label=target_names[label])
plt.title("t-SNE Projection")
plt.xlabel("t-SNE 1")
plt.ylabel("t-SNE 2")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()

This code runs both UMAP and t-SNE on the same data, helping you compare their visual outputs side by side.

Advantages

Faster than t-SNE: Scales to millions of points with less computational overhead.
Better Global Structure: Maintains relative distances between distant clusters.
Flexible Distance Metrics: Supports cosine, correlation, Jaccard, etc.
Usable for Preprocessing: Unlike t-SNE, UMAP embeddings can be used as features in ML models.

Limitations

Hyperparameter Sensitivity:
- \(n_{\text{neighbors}}\) controls local vs. global focus.
- \(\text{min_dist}\) determines how tightly points are packed.
- Poor tuning can lead to misleading visualizations.
Stochasticity: Like t-SNE, UMAP has randomness; results may vary unless seeds are fixed.
Not Truly Interpretable: Like other non-linear methods, axes have no semantic meaning.

In summary, UMAP combines mathematical elegance with practical flexibility. It preserves manifold structure, scales gracefully, and produces meaningful, interpretable visuals—making it a strong default for exploratory data visualization and even preprocessing pipelines. Up next: we’ll see how Autoencoders approach dimensionality reduction through neural networks and non-linear transformations.

4.3 Autoencoders

Autoencoders are a class of neural networks designed to learn compact, efficient representations of data in an unsupervised manner. Unlike PCA or UMAP, which rely on algebraic or topological techniques, autoencoders learn non-linear transformations using deep learning—making them incredibly powerful for high-dimensional and unstructured data like images, audio, or sequences.

At their core, autoencoders are not just used for dimensionality reduction—they are representation learners.

Core Concepts

An autoencoder consists of two main components:

Encoder: Maps input data to a compressed representation.
Decoder: Reconstructs the input from the compressed representation.

Formally, given an input vector \(x \in \mathbb{R}^d\), the encoder function \(f_\theta\) maps it to a latent vector:

\[z = f_\theta(x) \in \mathbb{R}^k, \quad k \ll d\]

The decoder \(g_\phi\) attempts to reconstruct the input:

\[\hat{x} = g_\phi(z)\]

The network is trained to minimize a reconstruction loss, typically the Mean Squared Error (MSE):

\[\mathcal{L}(x, \hat{x}) = \|x - \hat{x}\|_2^2\]

By constraining the bottleneck size (the latent dimension \(k\)), the network is forced to learn a compressed, informative encoding of the input.

Architecture Overview

The typical architecture looks like this:

Input → [Encoder Layers] → Bottleneck (Latent z) → [Decoder Layers] → Output (Reconstructed Input)

Encoder: Convolutional or dense layers that reduce dimensionality.
Latent Space: The compact, low-dimensional embedding.
Decoder: Mirrors the encoder to reconstruct the input.

This structure can be shallow or deep, depending on the complexity of the data.

Applications

Autoencoders are highly flexible and support numerous use cases:

Dimensionality Reduction: Learning embeddings for clustering or classification.
Denoising: Reconstructing clean inputs from corrupted versions (denoising autoencoders).
Anomaly Detection: Poor reconstruction signals deviations from normal patterns.
Pretraining: Using encoder weights to initialize deep networks.
Latent Space Visualization: Mapping images or sequences into 2D/3D space.

Python Implementation (Keras Example on MNIST)

Let’s use an autoencoder to compress and reconstruct handwritten digits from the MNIST dataset.

import numpy as np
import matplotlib.pyplot as plt
from tensorflow.keras.datasets import mnist
from tensorflow.keras.models import Model
from tensorflow.keras.layers import Input, Dense
from tensorflow.keras import regularizers

# Load MNIST data
(x_train, _), (x_test, _) = mnist.load_data()
x_train = x_train.astype("float32") / 255.
x_test = x_test.astype("float32") / 255.
x_train = x_train.reshape((len(x_train), -1))
x_test = x_test.reshape((len(x_test), -1))

# Define dimensions
input_dim = x_train.shape[1]
encoding_dim = 32  # latent dimension

# Encoder
input_img = Input(shape=(input_dim,))
encoded = Dense(128, activation='relu')(input_img)
encoded = Dense(encoding_dim, activation='relu')(encoded)

# Decoder
decoded = Dense(128, activation='relu')(encoded)
decoded = Dense(input_dim, activation='sigmoid')(decoded)

# Autoencoder model
autoencoder = Model(input_img, decoded)
autoencoder.compile(optimizer='adam', loss='mse')

# Train
autoencoder.fit(x_train, x_train,
                epochs=20,
                batch_size=256,
                shuffle=True,
                validation_data=(x_test, x_test))

Visualizing Reconstructions

You can evaluate how well the autoencoder performs by comparing original and reconstructed images:

decoded_imgs = autoencoder.predict(x_test)

n = 10  # show 10 digits
plt.figure(figsize=(20, 4))
for i in range(n):
    # Original
    ax = plt.subplot(2, n, i + 1)
    plt.imshow(x_test[i].reshape(28, 28), cmap='gray')
    plt.title("Original")
    plt.axis('off')

    # Reconstructed
    ax = plt.subplot(2, n, i + 1 + n)
    plt.imshow(decoded_imgs[i].reshape(28, 28), cmap='gray')
    plt.title("Reconstructed")
    plt.axis('off')
plt.tight_layout()
plt.show()

Variants of Autoencoders

Denoising Autoencoders (DAE):
- Trained to reconstruct original input from noisy versions.
- Useful for robust representation learning.
Variational Autoencoders (VAE):
- Introduce probabilistic constraints on latent space.
- Instead of mapping to a point \(z\), VAEs learn a distribution \(q(z \mid x)\).
- Enable generative modeling by sampling from latent space.
Objective:
\[\mathcal{L} = \mathbb{E}_{q(z|x)}[\log p(x|z)] - D_{KL}[q(z|x) \| p(z)]\]
where \(D_{KL}\) is the Kullback-Leibler divergence between the approximate posterior and the prior.

Limitations

Requires Large Data: Deep autoencoders need substantial training data and GPU resources.
Interpretability: Unlike PCA or LDA, the learned features (neurons) are not readily interpretable.
Sensitive to Architecture Choices: Latent space quality depends heavily on network depth, regularization, and optimizer tuning.
Overfitting Risk: Without proper regularization, the autoencoder may memorize input rather than generalize.

In essence, autoencoders mark the convergence of deep learning and representation theory. When your dataset is vast, non-linear, and unstructured—autoencoders provide a highly expressive, trainable way to compress, denoise, and analyze it. Up next, we’ll shift focus from learning projections to selecting features—exploring feature selection as a form of dimensionality reduction.

5. Feature Selection as Dimensionality Reduction

So far, we’ve explored techniques that transform data into lower-dimensional representations—either linearly (like PCA) or non-linearly (like UMAP or Autoencoders). But what if instead of transforming the features, we simply select a subset of them?

That’s the principle behind feature selection. Rather than projecting data onto new axes, we retain a smaller, more informative set of the original features. This approach preserves the semantic meaning of features—something that’s often lost in methods like PCA.

Feature selection is particularly valuable in high-dimensional, low-sample domains like genomics, where interpretability is crucial and irrelevant features are abundant.

5.1 L0-Based Feature Selection

Core Concepts

The most direct approach to feature selection is via the L0 norm—which counts the number of non-zero coefficients in a model:

\[\|w\|_0 = \text{Number of non-zero entries in } w\]

The ideal feature selection formulation for linear regression is:

\[\min_{w} \|y - Xw\|_2^2 + \lambda \|w\|_0\]

where:

\(X \in \mathbb{R}^{n \times d}\) is the design matrix,
\(y \in \mathbb{R}^n\) is the target,
\(w \in \mathbb{R}^d\) is the weight vector,
\(\lambda\) controls sparsity.

This objective aims to minimize prediction error while selecting as few features as possible.

However, minimizing the L0 norm is a combinatorial optimization problem—NP-hard in general. Recent advances like the L0Learn package (in R and Python) provide efficient, approximate solvers using coordinate descent with local combinatorial search.

Applications

L0-based selection shines in fields like:

Genomics: Selecting a few gene markers from tens of thousands of features.
Neuroscience: Pinpointing key neural signals or brain regions.
Finance: Identifying a compact set of predictors in asset pricing models.

These settings demand interpretable, sparse models, which L0 regularization delivers better than L1 or L2.

Python Implementation (with `l0bnb`)

While L0Learn is originally in R, equivalent Python libraries like l0bnb and scikit-feature can solve similar problems. Here’s a conceptual example using l0bnb:

# pip install l0bnb (if supported on your platform)

from l0bnb import L0BnBClassifier
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

# Simulate high-dimensional data
X, y = make_classification(n_samples=100, n_features=1000,
                           n_informative=10, random_state=42)

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

# L0 Feature Selection + Classification
model = L0BnBClassifier(max_nonzeros=10)
model.fit(X_train, y_train)
y_pred = model.predict(X_test)

print("Accuracy:", accuracy_score(y_test, y_pred))
print("Selected features:", model.selected_features_)

This example creates a sparse classification problem with only 10 relevant features out of 1000 and applies L0-based selection and classification simultaneously.

Advantages

Interpretability: Outputs a clear subset of selected features.
Sparsity: Models remain compact and fast at inference time.
Theoretical Optimality: Under certain conditions, L0 yields the best feature subset.

Limitations

Scalability: True L0 optimization is computationally expensive for large \(d\).
Model Dependency: Feature selection is often tied to a specific model or loss function.
Tooling: Compared to L1/L2, fewer stable, production-ready libraries exist in Python.

5.2 Other Feature Selection Methods

Beyond L0, there are three main categories of feature selection techniques: filter, wrapper, and embedded methods. Each offers different trade-offs between speed, interpretability, and predictive power.

Filter Methods

These methods rank features based on statistical criteria, independent of the learning algorithm.

Examples:

Variance Thresholding: Remove features with low variance.

from sklearn.feature_selection import VarianceThreshold
selector = VarianceThreshold(threshold=0.01)
X_new = selector.fit_transform(X)

Correlation Filtering: Select features highly correlated with the target.

import pandas as pd
corr = pd.Series(np.abs(np.corrcoef(X.T, y)[-1, :-1]))
top_features = corr.nlargest(20).index
X_selected = X[:, top_features]

Pros:

Fast, simple, model-agnostic.

Cons:

Ignores interactions or model performance.

Wrapper Methods

These use the model’s performance to evaluate subsets of features, usually via cross-validation.

Example: Recursive Feature Elimination (RFE)

from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression

estimator = LogisticRegression()
selector = RFE(estimator, n_features_to_select=20)
X_rfe = selector.fit_transform(X, y)

Pros:

Tailored to the model, can capture feature interactions.

Cons:

Computationally expensive.
Can overfit if not regularized.

Embedded Methods

These incorporate feature selection as part of model training via regularization or structure.

Example 1: L1 Regularization (Lasso)

Lasso minimizes:

\[\min_{w} \|y - Xw\|_2^2 + \lambda \|w\|_1\]

which induces sparsity in \(w\).

from sklearn.linear_model import LassoCV
model = LassoCV().fit(X, y)
X_lasso = X[:, model.coef_ != 0]

Example 2: Tree-Based Feature Importance

from sklearn.ensemble import RandomForestClassifier

model = RandomForestClassifier()
model.fit(X, y)
importances = model.feature_importances_
top_features = np.argsort(importances)[-20:]
X_tree = X[:, top_features]

Pros:

Efficient.
Works well with high-dimensional, non-linear data.

Cons:

May require threshold tuning.
L1-based models may be unstable when features are highly correlated.

Feature selection is a powerful alternative to dimensionality reduction. It not only simplifies models and improves performance but also retains interpretability—especially critical in high-stakes domains like healthcare, finance, or biology.

Whether you go for mathematically principled L0 selection, fast heuristics like variance filtering, or embedded models like Lasso and trees, the key is to balance parsimony with predictive power.

In the next section, we’ll look beyond individual features and explore clustering-based dimensionality reduction—like feature agglomeration and manifold-based embedding techniques.

6. Other Dimensionality Reduction Techniques

While PCA, t-SNE, UMAP, and Autoencoders dominate most dimensionality reduction workflows, there exists a rich ecosystem of specialized techniques tailored for certain data structures and objectives. This section explores three such techniques—Feature Agglomeration, Isomap, and Locally Linear Embedding (LLE)—each offering a unique perspective on reducing dimensions by leveraging clustering, geodesic distances, or local geometry.

6.1 Feature Agglomeration

Core Concepts

Feature Agglomeration is a clustering-based technique that reduces dimensionality by grouping similar features together. Unlike PCA or UMAP, which generate new abstract features, agglomeration combines correlated or redundant features into feature clusters and then averages them.

This method uses hierarchical clustering (usually Ward’s method) on the feature correlation matrix rather than on samples. Conceptually:

Compute pairwise similarity between features.
Build a hierarchical tree (dendrogram).
Merge similar features into clusters.
Replace each cluster with a single averaged feature.

This transforms the original matrix \(X \in \mathbb{R}^{n \times d}\) into \(X' \in \mathbb{R}^{n \times k}\), where \(k < d\).

Mathematical Intuition

Given features \(f_1, f_2, \dots, f_d\), we define similarity via a correlation metric or Euclidean distance:

\[\text{dist}(f_i, f_j) = \|f_i - f_j\|_2\]

Ward’s method then minimizes intra-cluster variance during merging:

\[\Delta E = \sum_{x \in C_i \cup C_j} \|x - \mu_{C_i \cup C_j}\|^2 - \sum_{x \in C_i} \|x - \mu_{C_i}\|^2 - \sum_{x \in C_j} \|x - \mu_{C_j}\|^2\]

Applications

Text Mining: Reducing the dimensionality of sparse TF-IDF matrices by merging redundant word features.
Image Processing: Grouping adjacent or correlated pixel regions in image patches.
Genomics: Merging expression profiles of co-regulated genes.

Python Implementation

from sklearn.datasets import load_digits
from sklearn.feature_extraction.image import grid_to_graph
from sklearn.cluster import FeatureAgglomeration
from sklearn.preprocessing import StandardScaler

# Load dataset
data = load_digits()
X = StandardScaler().fit_transform(data.data)

# Agglomerate features into 20 groups
agglo = FeatureAgglomeration(n_clusters=20)
X_reduced = agglo.fit_transform(X)

print("Original shape:", X.shape)
print("Reduced shape:", X_reduced.shape)

This reduces the original 64-pixel features in the digits dataset to 20 meta-features via clustering.

Limitations

Loss of Granularity: Fine-grained feature information is lost when averaging over clusters.
Not Suitable for Mixed Types: Works best with continuous features.
Interpretability: Feature clusters may not correspond to semantically meaningful dimensions.

6.2 Isomap

Core Concepts

Isomap (Isometric Mapping) is a non-linear dimensionality reduction technique that extends classical Multidimensional Scaling (MDS) by incorporating geodesic distances—distances measured along the manifold rather than straight lines in ambient space.

Isomap is ideal when data lies on a non-linear, curved manifold, like a spiral or a 3D surface embedded in higher dimensions.

Mathematical Intuition

Given a dataset \(X = \{x_1, x_2, \dots, x_n\}\), Isomap performs the following steps:

Construct a k-nearest neighbor graph using Euclidean distances.
Compute shortest path distances between all points in this graph using Dijkstra’s algorithm:
\[D_{ij} = \text{geodesic distance between } x_i \text{ and } x_j\]
Apply classical MDS to the distance matrix \(D\) to find a low-dimensional embedding.

MDS seeks points \(y_1, \dots, y_n \in \mathbb{R}^k\) such that:

\[\|y_i - y_j\|_2^2 \approx D_{ij}^2\]

This results in a mapping that preserves the intrinsic geometry of the data.

Applications

Robotics and Control Systems: Analyzing trajectories on manifolds (e.g., robot joint spaces).
Pose Estimation: Reducing high-dimensional joint angle space to a lower-dimensional latent space.
Visualization: Capturing manifold structure in complex datasets.

Python Implementation

from sklearn.datasets import load_digits
from sklearn.manifold import Isomap
import matplotlib.pyplot as plt

# Load data
digits = load_digits()
X = digits.data
y = digits.target

# Apply Isomap
iso = Isomap(n_neighbors=10, n_components=2)
X_iso = iso.fit_transform(X)

# Plot
plt.figure(figsize=(8, 6))
scatter = plt.scatter(X_iso[:, 0], X_iso[:, 1], c=y, cmap='Spectral', s=15)
plt.title("Isomap Projection of Digits Dataset")
plt.colorbar(scatter, label='Digit Class')
plt.grid(True)
plt.show()

Limitations

Sensitive to Noise and Outliers: Poorly connected graphs distort geodesic distances.
Computational Cost: Dijkstra’s algorithm and eigen decomposition are expensive.
Requires Dense Sampling: Sparse regions in the manifold degrade performance.

6.3 Locally Linear Embedding (LLE)

Core Concepts

Locally Linear Embedding (LLE) is another manifold learning technique that preserves the local geometry of data. Unlike Isomap, LLE focuses on linear reconstructions of each point from its neighbors.

Mathematical Intuition

Given data points \(x_1, \dots, x_n\) in high-dimensional space:

For each \(x_i\), find its \(k\) nearest neighbors.
Compute reconstruction weights \(w_{ij}\) such that:
\[x_i \approx \sum_{j} w_{ij} x_j \quad \text{subject to} \quad \sum_j w_{ij} = 1\]
These weights capture the local linear structure.
In the low-dimensional space, find points \(y_1, \dots, y_n\) that preserve the same weights:
\[y_i \approx \sum_{j} w_{ij} y_j\]

This leads to a sparse eigenvalue problem whose solution gives the embedding.

Applications

Image Manifolds: Reducing face pose or lighting variations to 2D latent structure.
Speech Signals: Uncovering intrinsic coordinates in time-frequency representations.
Handwriting: Separating digit styles and writing modes.

Python Implementation

from sklearn.manifold import LocallyLinearEmbedding
from sklearn.datasets import load_digits
import matplotlib.pyplot as plt

digits = load_digits()
X = digits.data
y = digits.target

lle = LocallyLinearEmbedding(n_neighbors=10, n_components=2)
X_lle = lle.fit_transform(X)

plt.figure(figsize=(8, 6))
scatter = plt.scatter(X_lle[:, 0], X_lle[:, 1], c=y, cmap='Spectral', s=15)
plt.title("LLE Projection of Digits Dataset")
plt.colorbar(scatter, label='Digit Class')
plt.grid(True)
plt.show()

Limitations

Poor Global Structure: LLE preserves local distances but may distort global shape.
Sensitive to k: Too small \(k\) may miss structure; too large violates local linearity.
Struggles with Non-Convex Manifolds: LLE may “tear” the manifold or collapse dimensions.

Summary

Technique	Core Idea	Best For	Limitations
Feature Agglomeration	Cluster similar features	Images, text	Loss of interpretability
Isomap	Preserve geodesic distances	Robotics, visualization	Sensitive to outliers
LLE	Preserve local geometry	Face/speech/image data	Sensitive to neighborhood size

These techniques provide more customized tools for dimensionality reduction—especially useful when working with structured, manifold-based, or domain-specific datasets. In the next section, we’ll look at practical considerations for choosing the right dimensionality reduction method and tuning it effectively.

7. Practical Considerations

As we’ve seen, the landscape of dimensionality reduction is rich and diverse—spanning linear methods, non-linear projections, and neural approaches. But the theoretical knowledge only takes you so far. Applying these methods effectively in real-world projects requires attention to practical trade-offs across dimensions such as interpretability, scale, supervision, and modeling goals.

This section outlines the key considerations that guide the practical selection, tuning, and deployment of dimensionality reduction techniques.

7.1 Choosing the Right Technique

Selecting the right dimensionality reduction strategy depends on the data structure, the task objective, and the constraints of your pipeline.

Linear vs. Non-Linear Methods

Use linear methods (e.g., PCA, LDA, Truncated SVD) when:
- Relationships are mostly linear.
- Interpretability or mathematical simplicity is desired.
- Speed and scalability are critical.
Use non-linear methods (e.g., t-SNE, UMAP, Autoencoders, LLE) when:
- The data lies on a curved manifold.
- You’re exploring intrinsic structure or visualizing complex clusters.
- Preserving local neighborhoods is more important than global variance.

Supervised vs. Unsupervised Settings

Unsupervised techniques (PCA, t-SNE, UMAP, Autoencoders) are suitable for:
- Visualization
- Clustering
- Preprocessing before unsupervised models
Supervised methods (LDA, supervised autoencoders) are better for:
- Classification problems
- Feature extraction tailored to target labels
- Situations requiring discriminative projections

Visualization vs. Modeling Goals

Use t-SNE and UMAP when your goal is visualizing high-dimensional data in 2D or 3D.
Use PCA, SVD, Lasso, Autoencoders when your goal is modeling or feature compression.
Don’t use t-SNE/UMAP embeddings as model inputs unless transformed carefully and consistently.

7.2 Preprocessing Before Dimensionality Reduction

Dimensionality reduction often magnifies data quality issues, making preprocessing essential.

Standardization and Normalization

PCA, LDA, and Autoencoders are sensitive to feature scale.

Always apply standardization (zero mean, unit variance):

from sklearn.preprocessing import StandardScaler
X_scaled = StandardScaler().fit_transform(X)

UMAP and t-SNE also benefit from standardization—especially with mixed-feature datasets.

Handling Missing Values

PCA and SVD require complete matrices.

Impute missing values before applying:

from sklearn.impute import SimpleImputer
imputer = SimpleImputer(strategy='mean')
X_filled = imputer.fit_transform(X)

Autoencoders can sometimes learn to denoise or reconstruct missing data directly with training supervision.

Categorical Variables

PCA and SVD cannot handle raw categorical data—use one-hot encoding or entity embeddings.
For high-cardinality categoricals:
- Use target encoding or hashing before applying Lasso, UMAP, or Autoencoders.

7.3 Hyperparameter Tuning

Different techniques require careful tuning to extract meaningful embeddings.

PCA, Truncated SVD

Tune the number of components based on:
- Explained variance:
  \[\text{Explained Variance Ratio} = \frac{\lambda_k}{\sum_{i=1}^d \lambda_i}\]
- Scree plot elbow method.
- Cumulative thresholds (e.g., 95% retained variance).

t-SNE

Key parameter: Perplexity (typically 5–50).
Controls the effective number of neighbors.
Try multiple values and evaluate stability of structure.

UMAP

Tune:
- n_neighbors (locality vs. globality)
- min_dist (cluster tightness)
Larger n_neighbors → smoother manifold, better global separation.
Smaller min_dist → tighter local clusters.

Autoencoders

Tune:
- Bottleneck dimension (latent space size)
- Depth and width of encoder/decoder
- Learning rate, batch size, regularization

7.4 Evaluation Metrics

How do you know if your dimensionality reduction method is effective?

Linear Methods

PCA, SVD: Look at explained variance ratio.
LDA: Evaluate classification performance using projected data.

Autoencoders

Reconstruction Error:
\[\mathcal{L}(x, \hat{x}) = \|x - \hat{x}\|^2\]
Lower error = better compression fidelity.
Compare errors across models with different latent sizes.

Manifold Methods (t-SNE, UMAP, LLE)

Trustworthiness and Continuity: Metrics that quantify how well neighborhoods are preserved between high- and low-dimensional spaces.
Visual Coherence: Are clusters clearly separated? Is structure meaningful?

7.5 Scalability and Performance

Large-scale datasets pose real challenges for many DR algorithms.

Incremental PCA

Works well with streaming data or datasets that don’t fit into memory.

Uses batch-wise computation:

from sklearn.decomposition import IncrementalPCA
ipca = IncrementalPCA(n_components=50, batch_size=200)

Truncated SVD

Efficient for sparse matrices (e.g., TF-IDF in NLP).
Doesn’t require centering—saves time and memory.

UMAP

Can handle millions of samples.
GPU-accelerated implementations available via Rapids.ai (cuml.UMAP).

Autoencoders

Train on GPU for speed and scalability.
Use data generators for large datasets.
Can be embedded in model pipelines (e.g., compress before feeding to classifier).

In practice, successful dimensionality reduction requires balancing interpretability, computational cost, fidelity, and downstream utility. There’s no one-size-fits-all. But with these guiding principles, you’ll be well-equipped to reduce, visualize, and model high-dimensional data in your workflows.

8. Challenges and Pitfalls

While dimensionality reduction is a powerful tool in any data scientist’s arsenal, it comes with its own set of challenges and pitfalls. Failing to account for them can lead to misleading insights, degraded model performance, or unjustified complexity. Let’s unpack the key caveats.

8.1 Overfitting in High Dimensions

High-dimensional datasets often suffer from the curse of dimensionality:

Distance metrics become less meaningful.
Sparsity increases, degrading model generalization.
Models can overfit noise, especially when the number of features far exceeds the number of samples.

Dimensionality reduction mitigates this by projecting data into a lower-dimensional space, removing noise and redundant features, thus improving generalization.

For example, PCA identifies orthogonal directions of maximum variance, compressing the dataset to its most informative components, while autoencoders filter representations through a bottleneck that acts as a natural regularizer.

8.2 Loss of Interpretability

Techniques like PCA, UMAP, or autoencoders create new latent features, which are abstract transformations of the original variables.

In PCA, principal components are linear combinations:
\[\text{PC}_1 = a_1 x_1 + a_2 x_2 + \dots + a_d x_d\]
But these axes are difficult to interpret semantically.
In non-linear methods like t-SNE or UMAP, axes have no inherent meaning at all.

This loss of interpretability may be acceptable in exploratory data analysis but problematic in regulated industries (e.g., healthcare, finance), where explainability is non-negotiable.

8.3 Hyperparameter Sensitivity

Many DR techniques are highly sensitive to hyperparameter tuning:

t-SNE: Small changes in perplexity or learning rate can drastically alter the structure of the output.
UMAP: The n_neighbors and min_dist parameters significantly impact the balance between local and global structure.
Autoencoders: The number of layers, bottleneck size, and optimizer settings can affect reconstruction and embedding quality.

Poor tuning can result in:

Over-clustered or overly dispersed visualizations.
Loss of important structure or variance.
Artifacts in embeddings that don’t reflect real data patterns.

8.4 Computational Cost

PCA is efficient for small-to-medium datasets, but struggles with large, dense matrices.
t-SNE is O(n²) in complexity—prohibitively slow on large datasets.
Autoencoders require GPU acceleration, especially for image or sequence data.
Incremental PCA and Truncated SVD offer scalable alternatives, but may lose some variance capture or precision.

Always weigh speed vs. accuracy depending on whether your use case is exploratory, production-level, or real-time.

9. Best Practices and Guidelines

To get the most out of dimensionality reduction—and avoid the above pitfalls—follow these time-tested best practices.

9.1 When to Use Each Technique

Goal	Recommended Technique
Linearly structured data	PCA, Truncated SVD
Sparse high-dim matrices	Truncated SVD (e.g., TF-IDF)
Class separation needed	LDA
Visualization	t-SNE, UMAP
Deep feature extraction	Autoencoders
Interpretable models	Feature selection, Lasso, L0

Choose methods based on data structure, task goal, interpretability needs, and scalability constraints.

9.2 Avoiding Common Mistakes

❌ Skipping Standardization for PCA: PCA assumes zero-centered and scaled features. Skipping this step skews the component directions toward features with larger scales.
❌ Using t-SNE for Downstream Modeling: t-SNE is non-parametric and stochastic; you can’t project new test data easily. It’s strictly for visualization.
❌ Applying DR Before Cleaning: Outliers and missing values distort results. Always impute, scale, and sanitize your data first.
❌ Over-compressing: Reducing to too few dimensions may discard important signals. Evaluate explained variance or reconstruction error.

9.3 Workflow Integration

Integrate dimensionality reduction into your ML pipeline using tools like sklearn.pipeline.Pipeline. This ensures:

Reproducibility across train/test splits.
Avoidance of data leakage.
Modular experimentation.

Example:

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from sklearn.ensemble import RandomForestClassifier

pipeline = Pipeline([
    ('scaling', StandardScaler()),
    ('pca', PCA(n_components=20)),
    ('clf', RandomForestClassifier())
])

9.4 Reporting Results

Good reporting ensures transparency and trust in your dimensionality reduction process.

Visualize reduced dimensions using scatter plots, especially for t-SNE, UMAP, or LDA.
Report explained variance for PCA/SVD:
\[\text{Cumulative Explained Variance} = \sum_{i=1}^k \frac{\lambda_i}{\sum_j \lambda_j}\]

Log reconstruction error for autoencoders:

mse = np.mean(np.square(X_original - X_reconstructed))

Annotate plots with class labels or cluster assignments where relevant.

Wrapping Up

Dimensionality reduction is a critical step in modern data workflows—not for aesthetic compression, but for achieving better model generalization, improved training speed, and interpretability where feasible.

As we’ve seen, no single technique fits all use cases. Linear methods like PCA and SVD are well-suited for structured data and fast modeling pipelines. Non-linear methods such as t-SNE and UMAP provide meaningful visualizations when exploring complex relationships. Autoencoders offer flexibility for non-linear compression in deep learning contexts, while feature selection techniques preserve interpretability and can enhance model stability.

Choosing the right approach depends on multiple factors: data shape, sparsity, downstream task, interpretability needs, and computational constraints. Tuning hyperparameters, preprocessing correctly, and validating results are essential to avoid misleading reductions.

In practice, dimensionality reduction should be treated as an iterative, goal-driven process—one that aligns with your broader modeling or analysis objectives. Whether used for visualization, noise removal, feature compression, or pipeline optimization, its impact on both performance and insight can be substantial when applied thoughtfully.

1. Introduction

1.1 Definition and Importance

1.2 The Curse of Dimensionality

1.3 Goals of Dimensionality Reduction

1.4 Applications of Dimensionality Reduction

2. Theoretical Foundations

2.1 Linear Algebra Basics

Covariance Matrix

Eigen Decomposition

Singular Value Decomposition (SVD)

2.2 Manifold Learning

2.3 Distance Metrics in High Dimensions

Euclidean Distance

Manhattan Distance

Cosine Similarity

Curse of Dimensionality

2.4 Variance and Information Retention

Explained Variance

Bias–Variance Trade-off

3. Linear Dimensionality Reduction Techniques

3.1 Principal Component Analysis (PCA)

Core Concepts

Eigen Decomposition of the Covariance Matrix

Projection and Variance

Step-by-Step Process

Step 1: Standardize the Data

Step 2: Compute Covariance Matrix

Step 3: Eigen Decomposition

Step 4: Project Data

Applications

Limitations

Python Implementation

Variants of PCA

Incremental PCA

Kernel PCA

3.2 Truncated Singular Value Decomposition (SVD)

Core Concepts

PCA vs. Truncated SVD

Applications

Python Implementation on Sparse Text Data

Advantages

Limitations

3.3 Linear Discriminant Analysis (LDA)

Core Concepts

Intuition

Applications

Python Implementation on a Classification Task

Limitations

4. Non-Linear Dimensionality Reduction Techniques

4.1 t-Distributed Stochastic Neighbor Embedding (t-SNE)

Core Concepts

Mathematical Intuition

Perplexity and Its Impact

Applications

Python Implementation

Limitations

Best Practices

4.2 Uniform Manifold Approximation and Projection (UMAP)

Core Concepts

Mathematical Foundations

Local and Global Structure

Applications

Python Implementation

Advantages

Limitations

4.3 Autoencoders

Core Concepts

Architecture Overview

Applications

Python Implementation (Keras Example on MNIST)

Visualizing Reconstructions

Variants of Autoencoders

Limitations

5. Feature Selection as Dimensionality Reduction

5.1 L0-Based Feature Selection

Core Concepts

Applications

Python Implementation (with l0bnb)

Advantages

Limitations

Python Implementation (with `l0bnb`)