k-means++ অ্যালগরিদম

k-means++ clustering ব্যাবহার করে আমরা বেশিরভাগ unsupervised learning এর ক্ষেত্রে k-means clustering এর তুলনায় বেশি দ্রুত এবং অধিকতর নিকট সমাধান পেতে পারি। যেহেতু unsupervised learning এর ক্ষেত্রে কোনও সুনির্দিষ্ট সমাধান থাকে না, তাই যেকোনো unsupervised learning এই আমরা চেষ্টা করি cost কমানোর যেটি k-means++ খুবই দক্ষতার সাথে করে।

David Arthur এবং Sergei Vassilvitskii ২০০৭ সালে k-means++ অ্যালগরিদমটির প্রস্তাব দেন standard k-means থেকে clustering এর NP-hard সমাধান হিসাবে।

Standard k-means algorithm এর অপূর্ণতা

k-means++ শেখার আগে আমাদের জেনে নেওয়া ভাল standard k-means algorithm এর ত্রুটি এবং এর অপূর্ণতাগুলি।

১/ কিছু ক্ষেত্রে k-means বহুবার iterated হয় যা algorithm টাকে ধীর করে দেয়।

২/ k-means কেমন কাজ করবে তা বেশিরভাগটাই নির্ভর করে আমরা প্রাথমিক ভাবে যে cluster center গুলো এলোমেলোভাবে নির্বাচন করেছি তার উপর। এটির কারণেই কখনো কখনো k-means একই cluster এ দুটি cluster center নির্বাচন করে ফেলে। এটি উপযুক্ত উদাহরণ দিয়ে বোঝা যাক।

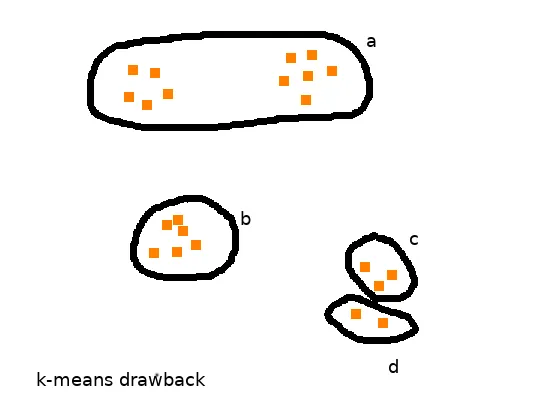
এক্ষেত্রে ‘a’ cluster এ বাস্তবে 2 টি cluster থাকলেও k-means তা নির্ধারণ করতে অক্ষম। একইসাথে এটি ‘c’ ও ‘d’ cluster কে আলাদা বললেও তা আসলে একটিই cluster। এভাবেই k-means কখনো কখনো local optimum এই সীমাবদ্ধ থেকে যায় এবং তা bad cluster সৃষ্টি করে।

k-means++ algorithm

এবার আসা যাক k-means++ algorithm এ এবং এটি কেমন কার্যকরী ভাবে clustering করে।

কোনো data set থেকে আমরা নিম্নোক্ত উপায়ে clustering করতে পারি।

১ক/ প্রথমেই আমরা randomly একটি cluster center নির্ধারণ করি data set থেকে। (uniform and random choice)

১খ/ এখন data set এর থেকে পরবর্তী center টি নির্ধারণ করতে আমরা furthest point strategy ব্যাবহার করি।

এই পদ্ধতিতে আমরা কোনো point কে তখনি একটি cluster center নির্বাচন করি যখন সেটি পূর্ব নির্ধারিত cluster center থেকে সবথেকে বেশি দুরে অবস্থান করে।

এটি গাণিতিকভাবে নির্ণয় করতে আমরা একটি নতুন চল ধরব D(x) যা হল কোনো data point থেকে ইতিমধ্যে নির্বাচিত cluster center গুলোর দূরত্ব গুলোর মধ্যে নিম্নতমটি (min c∈C abs(x − c))। এখন পরবর্তী cluster center নির্ধারণ করার সময় আমরা data point গুলোর মধ্যে সেটিকে নির্বাচন করব যার ক্ষেত্রে D(x)²/ΣD(x)² এই সম্ভাবনা টা বেশি। (furthest point strategy)

নীচে একটি উদাহারণ দিলে বিষয়টি আরও পরিষ্কার হয়ে যাবে। (ক্রমশ)

২/ আমরা এই ভাবে cluster center নির্বাচন করব যতক্ষণ আমাদের কাছে k টি cluster center আসে।

৩/ এভাবে cluster center initialisation এর পর আমরা প্রত্যেক data point কে তার নিকটতম cluster center এর সংশ্লিষ্ট cluster এ অন্তর্ভুক্ত করবো, যেমন ভাবে আমরা k-means algorithm এ করে থাকি।

আমরা এই data points allocation ততক্ষণ করবো যতক্ষণ না cluster center গুলো অপরিবর্তিত থাকছে।

উদাহরণ

এবার একটি 1 dimensional data points নিয়ে k-means++ algorithm টি ঝালিয়ে নেওয়া যাক।

ধরা যাক আমাদের কাছে data points আছে {0, 1, 2, 5, 6} এবং আমরা ২ টি cluster এই data points থেকে পেতে চাই। (k = 2)

প্রথম cluster center C1 হল 0। C1 = 0 (প্রথম cluster center টি আমরা অনির্দিষ্ট ভাবে প্রথম data point টাকে নেব)

এখন দ্বিতীয় cluster center নির্বাচনের ক্ষেত্রে আমরা D(x)²/ΣD(x)² এই সম্ভাবনা টা প্রতিটি data point এর জন্য নির্ণয় করবো।

P(C2=1) = ((1–0)²)f = 1f নিকটতম cluster center, C1=0

P(C2=2) = ((2–0)²)f = 4f নিকটতম cluster center, C1=0

P(C2=5) = ((5–0)²)f = 25f নিকটতম cluster center, C1=0

P(C2=6) = ((6–0)²)f = 36f নিকটতম cluster center, C1=0

এখানে f = (1+4+25+36)

দেখা যাচ্ছে P(C2=6) সবথেকে বেশি, তাই k-means++ 6 কে C2 হিসাবে নির্বাচন করবে। C2 = 6

এরপর আমরা data point গুলোকে সবথেকে কাছের সংশ্লিষ্ট cluster center এর সাথে যুক্ত করলেই দুটি cluster পেয়ে যাব {(0, 1, 2)(5, 6)} ।

অন্য একটি উদাহরণ নিয়ে দেখা যাক।

ধরা যাক আমাদের কাছে data points আছে

{0, 1, 2, 5, 6, 9, 10} এবং আমরা ৩ টি cluster এই data points থেকে পেতে চাই। (k = 3)

প্রথম cluster center C1 হল 0। C1 = 0

দ্বিতীয় cluster center নির্বাচনের ক্ষেত্রে প্রথম উদাহরণের মতই আমরা furthest point 10 কে C2 হিসাবে নির্বাচন করবো। C2 = 10

এখন তৃতীয় cluster center এর জন্য আমাদেরকে সংশ্লিষ্ট সম্ভাবনা গুলো নির্ণয় করতে হবে প্রতিটি data point এর জন্য।

P(C3=1) = ((1–0)²)f = 1f নিকটতম cluster center, C1=0

P(C3=2) = ((2–0)²)f = 4f নিকটতম cluster center, C1=0

P(C3=5) = ((5–0)²)f = 25f নিকটতম cluster center, C1=0

P(C3=6) = ((6–10)²)f = 16f নিকটতম cluster center, C2=10

P(C3=9) = ((9–10)²)f = 1f নিকটতম cluster center, C2=10

এখানে f = (1+4+25+16+1)

দেখা যাচ্ছে P(C3=5) সবথেকে বেশি, তাই k-means++ 5 কে C3 হিসাবে নির্বাচন করবে। C3 = 5

এরপর আমরা data point গুলোকে সবথেকে কাছের সংশ্লিষ্ট cluster center এর সাথে সংযুক্ত করলেই তিনটি cluster পেয়ে যাব। {(0, 1, 2)(5, 6)(9, 10)}

এভাবেই 2 dimensional বা উচ্চতর dimension এ আমরা k-means++ ব্যাবহার করে clustering করতে পারি। তথ্যগতভাবে বলা যেতে পারে k-means এবং k-means++ এর মধ্যে cluster center initialisation এরই শুধু পার্থক্য রয়েছে, বাকি প্রক্রিয়া দুক্ষেত্রেই এক।

k-means++ algorithm এর কার্যকারিতা

এখন k-means algorithm এর থেকে k-means++ কতটা কার্যকর তা দেখা যাক।

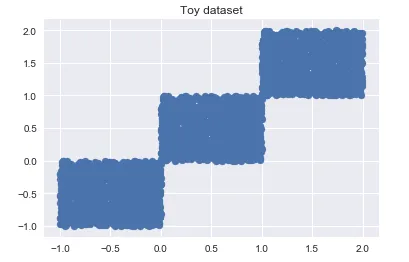
এখানে একটি dataset এর scatter plot দেওয়া হল

এবার k-means এবং k-means++ এর জন্য cluster center initialisation এর 2 dimensional histogram দেখা যাক

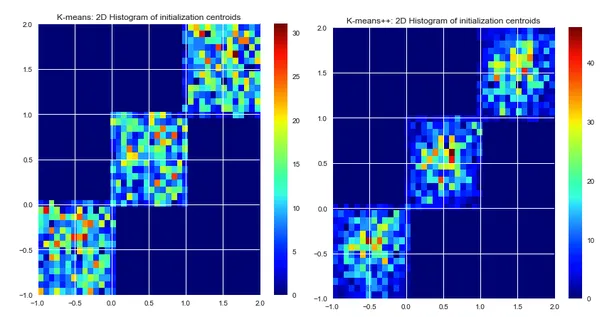
এর থেকে পরিষ্কার ভাবে বোঝা যায় k-means++ cluster গুলোর মধ্যভাগে বেশি initialise করেছে যা বেশিরভাগ dataset এর জন্য দ্রুত হবে এবং অধিকতর সঠিক cluster বানাতে সক্ষম হবে।

k-means++ এর অপূর্ণতা

K-means++ সম্পর্কে আলোচনা শেষ করার পূর্বে এটির কিছু ত্রুটি দেখে নেওয়া দরকার যা বাস্তব data set গুলোতে ব্যাবহারের ক্ষেত্রে দেখা দিতে পারে।

১/ k-means++ বিচ্ছিন্ন data point এর ক্ষেত্রে খুবই সংবেদনশীল (sensitive to outliers)। কারণ k-means++ সবসময় furthest point strategy ব্যাবহার করে cluster center গুলো নির্বাচন করে, যা করতে গিয়ে কিছুক্ষেত্রে তা বিচ্ছিন্ন একটি point কে cluster center নির্বাচন করে ফেলে যা কোন cluster সৃষ্টি করতে তেমন কোন গুরুত্ব রাখে না।

২/ ধরা যাক কোন Game Developer Company তাদের game খেলে, এমন যত gamer আছে, তাদের পছন্দের game genre(List of video game genres — Wikipedia) গুলো দিয়ে clustering করতে আগ্রহী। এখন game genre এর সংখ্যা অনেক বেশি হওয়ায় k-means++ cluster center initialisation এর জন্য ঠিক ততবারই data point গুলোর মধ্যে algorithm টিকে pass করাবে। সেক্ষেত্রে প্রক্রিয়াটি মন্থর হয়ে যাবে। k-means++ k সংখ্যক বার data point pass করার জন্য যেখানে k একটি অনেক বড় সংখ্যা তখন দ্রুত কাজ করে না। এটি অতিক্রম করতে আমরা oversampling এর সাহায্য নিই এবং এর থেকে k-means এর অন্য একটি ভিন্নতা — parallel k-means এর উৎপত্তি (http://theory.stanford.edu/~sergei/papers/vldb12-kmpar.pdf)।

এসব সত্ত্বেও বেশিরভাগ data set এর জন্য k-means++ তথাকথিত k-means algorithm এর থেকে বেশি সফল ভাবে clustering করতে সক্ষম।