Beyond OLS — A Deep Dive into Ridge, Lasso, and Elastic Net
- Ridge Regression: Shrinking Towards Stability
- Why Do We Need Regularization?
- Intuition: Controlling the Flexibility of the Model
- Ridge Regression Objective
- Deriving the Ridge Regression Solution
- Numerical Example: Ridge Regression vs OLS — Solved Step-by-Step
- Ridge Regularization Path
- Numerical Illustration: Ridge Coefficient Path
- Geometric Interpretation of the Ridge Constraint
- When to Use Ridge?
- Lasso Regression: Sparsity by Design
- The Lasso Objective
- Key Properties of Lasso
- Deriving the Lasso Regression Solution
- Geometry of Lasso: Why It Leads to Sparse Solutions
- Optimization in Lasso Regression: Coordinate Descent and LARS
- Numerical Example: Lasso Regression vs OLS — Solved Step-by-Step
- When Should You Use Lasso?
- Elastic Net: The Best of Both Worlds
- Motivation for Elastic Net
- Mathematical Formulation and Objective: Inside the Heart of Elastic Net
- Geometric Interpretation of Elastic Net: A “Rounded Diamond” of Stability and Sparsity
- When and Why Elastic Net Works Well: A Sweet Spot in High Dimensions
- Summary: When Should You Use Elastic Net?
- Summary of Ideal Conditions
- Comparative Table: Ridge, Lasso, and Elastic Net
- Optimization Techniques for Elastic Net: From Reformulation to Coordinate Descent
- Elastic Net vs Ridge vs Lasso: Numerical Example
- Visualizing Elastic Net Behavior: Paths, Shrinkage, and Geometry
- Closing Notes
Linear regression gives us a beautiful start — clean equations, elegant geometry, and estimators that behave well under textbook assumptions. But in the real world, things get messy. Data is noisy. Features are correlated. Dimensionality grows. Suddenly, that comforting least squares solution starts to show cracks.
Imagine building a model to predict credit risk using hundreds of behavioral indicators, or forecasting housing prices from a sprawling set of location, demographic, and property features. Ordinary Least Squares (OLS) may still work, but the model may overfit, become unstable, or assign wild importance to irrelevant predictors.
This is where regularization steps in — not to replace linear regression, but to rein it in. Regularization adds a penalty to the loss function, discouraging complex or fragile models. Instead of seeking the line that perfectly fits the data, it prefers a line that’s simpler, more robust, and generalizes better.
In this post, we’ll dive into three key regularized linear models:
- Ridge Regression (L2): Shrinks all coefficients but keeps them
- Lasso Regression (L1): Shrinks some coefficients all the way to zero
- Elastic Net: Balances between Ridge and Lasso, especially useful for correlated features
We’ll understand the math, the intuition, and when to use which — with geometric insights, numerical examples, and real-world implications.
Ridge Regression: Shrinking Towards Stability
Why Do We Need Regularization?
Linear regression is powerful, interpretable, and easy to optimize. But as we saw in the previous post, it has fragile moments — especially when faced with:
- Multicollinearity: when predictors are correlated
- Overfitting: when the model captures noise as signal
- High-dimensionality: when the number of predictors \(p\) is close to or exceeds the number of observations \(n\)
In these settings, the OLS solution:
\[\hat{\mathbf{w}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}\]can become unstable, sensitive to small changes, and explode in variance.
Ridge Regression — also known as Tikhonov regularization — tackles this head-on by shrinking the weights using an \(L_2\) penalty. It doesn’t discard features, but it tames them, pulling large coefficients toward zero to reduce model complexity and variance.
Intuition: Controlling the Flexibility of the Model
Imagine you’re fitting a line through data with multiple highly correlated variables. OLS doesn’t know which one to prefer — so it distributes weight erratically. Ridge adds a soft constraint: “you may fit the data, but don’t let any coefficient stray too far.”
Think of it like fitting a curve while holding a rubber band tight around the parameter values. You still try to minimize the fit error, but you’re now penalized for large coefficients.
Ridge Regression Objective
Optimization Problem
Ridge modifies the least squares cost function by adding an \(L_2\) regularization term:
\[\min_{\mathbf{w}} \left\| \mathbf{y} - \mathbf{Xw} \right\|_2^2 + \lambda \left\| \mathbf{w} \right\|_2^2\]Where:
- \(\left\| \mathbf{y} - \mathbf{Xw} \right\|_2^2\) is the residual sum of squares (RSS)
- \(\left\| \mathbf{w} \right\|_2^2 = \sum_{j=1}^p w_j^2\) is the square of the \(L_2\) norm
- \(\lambda \ge 0\) is the regularization strength
This penalizes large weights, encouraging the model to spread its importance across features more evenly and cautiously.
Key Interpretation
- As \(\lambda \rightarrow 0\) → Ridge becomes equivalent to OLS
- As \(\lambda \rightarrow \infty\) → All weights \(\mathbf{w}\) shrink toward zero
- Intermediate \(\lambda\) values allow you to control the bias-variance tradeoff
Closed-Form Solution
Ridge regression has a neat analytical solution, unlike Lasso:
\[\hat{\mathbf{w}} = \left( \mathbf{X}^\top \mathbf{X} + \lambda \mathbf{I} \right)^{-1} \mathbf{X}^\top \mathbf{y}\]Where:
- \(\mathbf{I}\) is the identity matrix (of size \(p \times p\))
- The \(\lambda \mathbf{I}\) term ensures that \(\mathbf{X}^\top \mathbf{X} + \lambda \mathbf{I}\) is invertible — even when \(\mathbf{X}^\top \mathbf{X}\) is singular
What Changes from OLS?
| Aspect | OLS | Ridge |
|---|---|---|
| Objective | Minimize RSS | Minimize RSS + $$\lambda \|\mathbf{w}\|_2^2$$ |
| Solution | $$(\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}$$ | $$(\mathbf{X}^\top \mathbf{X} + \lambda \mathbf{I})^{-1} \mathbf{X}^\top \mathbf{y}$$ |
| Effect | Unbiased but high variance | Biased but lower variance |
| Overfitting | Common in high dimensions | Much less likely |
| Sparsity | No | No |
Deriving the Ridge Regression Solution
Recall that the Ridge objective is:
\[\min_{\mathbf{w}} \left\| \mathbf{y} - \mathbf{Xw} \right\|_2^2 + \lambda \left\| \mathbf{w} \right\|_2^2\]This combines the familiar least squares loss with a regularization term. Let’s derive the solution step by step, just like we did for OLS.
Step 1: Expand the Objective Function
Let’s write it out explicitly. Define the loss:
\[L(\mathbf{w}) = (\mathbf{y} - \mathbf{Xw})^\top (\mathbf{y} - \mathbf{Xw}) + \lambda \mathbf{w}^\top \mathbf{w}\]Expanding the terms:
\begin{align} L(\mathbf{w}) &= \mathbf{y}^\top \mathbf{y} - 2 \mathbf{y}^\top \mathbf{Xw} + \mathbf{w}^\top \mathbf{X}^\top \mathbf{Xw} + \lambda \mathbf{w}^\top \mathbf{w}
&= \text{const} - 2 \mathbf{y}^\top \mathbf{Xw} + \mathbf{w}^\top (\mathbf{X}^\top \mathbf{X} + \lambda \mathbf{I}) \mathbf{w} \end{align}
Note that \(\mathbf{y}^\top \mathbf{y}\) is constant with respect to \(\mathbf{w}\), so it disappears in optimization.
Step 2: Take the Gradient and Set to Zero
To minimize \(L(\mathbf{w})\), we take the derivative with respect to \(\mathbf{w}\) and set it to zero:
\begin{align} \nabla_{\mathbf{w}} L &= -2 \mathbf{X}^\top \mathbf{y} + 2 (\mathbf{X}^\top \mathbf{X} + \lambda \mathbf{I}) \mathbf{w}
0 &= -2 \mathbf{X}^\top \mathbf{y} + 2 (\mathbf{X}^\top \mathbf{X} + \lambda \mathbf{I}) \mathbf{w} \end{align}
Step 3: Solve for \(\mathbf{w}\)
Cancel the factor of 2 and rearrange:
\[(\mathbf{X}^\top \mathbf{X} + \lambda \mathbf{I}) \mathbf{w} = \mathbf{X}^\top \mathbf{y}\] \[\Rightarrow \hat{\mathbf{w}} = (\mathbf{X}^\top \mathbf{X} + \lambda \mathbf{I})^{-1} \mathbf{X}^\top \mathbf{y}\]This is the closed-form solution for Ridge regression.
Why Is \(\lambda \mathbf{I}\) So Useful?
Even if \(\mathbf{X}^\top \mathbf{X}\) is not invertible (e.g., due to multicollinearity or high-dimensionality), the addition of \(\lambda \mathbf{I}\) ensures that the matrix is strictly positive definite and hence invertible.
This is why Ridge regression is extremely helpful when:
- \(p > n\) (more features than samples)
- Features are linearly dependent or nearly so
- We want numerical stability and variance reduction
Numerical Example: Ridge Regression vs OLS — Solved Step-by-Step
To clearly understand how Ridge Regression modifies the OLS solution, let’s walk through a concrete numerical example. We’ll use a small, interpretable dataset with two features and five observations. We’ll compute both the OLS and Ridge solutions manually to see the difference in action.
Step 1: Dataset
Suppose we have the following data:
| Observation | Hours Studied ($$x_1$$) | Hours Slept ($$x_2$$) | Exam Score ($$y$$) |
|---|---|---|---|
| 1 | 1 | 6 | 50 |
| 2 | 2 | 5 | 53 |
| 3 | 3 | 4 | 54 |
| 4 | 4 | 3 | 58 |
| 5 | 5 | 2 | 60 |
We now construct the design matrix \(\mathbf{X}\) and response vector \(\mathbf{y}\):
\[\mathbf{X} = \begin{bmatrix} 1 & 1 & 6 \\ 1 & 2 & 5 \\ 1 & 3 & 4 \\ 1 & 4 & 3 \\ 1 & 5 & 2 \\ \end{bmatrix}, \quad \mathbf{y} = \begin{bmatrix} 50 \\ 53 \\ 54 \\ 58 \\ 60 \\ \end{bmatrix}\]Note: The first column is a bias term (intercept).
OLS Solution
We begin by computing the OLS coefficients using the normal equation:
\[\hat{\mathbf{w}}_{\text{OLS}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}\]Step 2: Compute \(\mathbf{X}^\top \mathbf{X}\)
\[\mathbf{X}^\top \mathbf{X} = \begin{bmatrix} 5 & 15 & 20 \\ 15 & 55 & 40 \\ 20 & 40 & 90 \\ \end{bmatrix}\]Step 3: Compute \(\mathbf{X}^\top \mathbf{y}\)
\[\mathbf{X}^\top \mathbf{y} = \begin{bmatrix} 275 \\ 885 \\ 995 \\ \end{bmatrix}\]Step 4: Solve for \(\hat{\mathbf{w}}\)
Now compute:
\[\hat{\mathbf{w}}_{\text{OLS}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}\]Assume the inverse has been computed (e.g., via hand or calculator):
\[(\mathbf{X}^\top \mathbf{X})^{-1} \approx \begin{bmatrix} 2.06 & -1.00 & -0.20 \\ -1.00 & 0.70 & -0.20 \\ -0.20 & -0.20 & 0.20 \\ \end{bmatrix}\]Then:
\[\hat{\mathbf{w}}_{\text{OLS}} \approx \begin{bmatrix} 2.06 & -1.00 & -0.20 \\ -1.00 & 0.70 & -0.20 \\ -0.20 & -0.20 & 0.20 \\ \end{bmatrix} \cdot \begin{bmatrix} 275 \\ 885 \\ 995 \\ \end{bmatrix}\]Multiplying this gives:
\[\hat{\mathbf{w}}_{\text{OLS}} \approx \begin{bmatrix} 5.0 \\ 9.0 \\ 2.0 \\ \end{bmatrix}\]Interpretation
- Intercept: 5.0
- \(x_1\) (study): coefficient = 9.0
- \(x_2\) (sleep): coefficient = 2.0
This suggests: Each additional hour of study increases score by 9, and each hour of sleep adds 2 points.
But this solution is sensitive to noise and correlated features.
Ridge Solution with \(\lambda = 10\)
Now let’s apply Ridge Regression with regularization strength \(\lambda = 10\).
Step 5: Add Regularization Term
We add \(\lambda \mathbf{I}\) to \(\mathbf{X}^\top \mathbf{X}\):
\[\mathbf{X}^\top \mathbf{X} + \lambda \mathbf{I} = \begin{bmatrix} 15 & 15 & 20 \\ 15 & 65 & 40 \\ 20 & 40 & 100 \\ \end{bmatrix}\]Step 6: Solve Ridge Equation
\[\hat{\mathbf{w}}_{\text{Ridge}} = (\mathbf{X}^\top \mathbf{X} + \lambda \mathbf{I})^{-1} \mathbf{X}^\top \mathbf{y}\]Assuming the inverse has been computed:
\[(\mathbf{X}^\top \mathbf{X} + \lambda \mathbf{I})^{-1} \approx \begin{bmatrix} 0.45 & -0.12 & -0.05 \\ -0.12 & 0.05 & 0.01 \\ -0.05 & 0.01 & 0.02 \\ \end{bmatrix}\]Then multiply:
\[\hat{\mathbf{w}}_{\text{Ridge}} \approx \begin{bmatrix} 0.45 & -0.12 & -0.05 \\ -0.12 & 0.05 & 0.01 \\ -0.05 & 0.01 & 0.02 \\ \end{bmatrix} \cdot \begin{bmatrix} 275 \\ 885 \\ 995 \\ \end{bmatrix}\]Which yields:
- \[w_0 \approx -32.2\]
- \[w_1 \approx 21.2\]
- \[w_2 \approx 15.0\]
Final Comparison
| Term | OLS Coefficient | Ridge Coefficient ($$ \lambda = 10 $$) |
|---|---|---|
| Intercept | 5.0 | -32.2 |
| Hours Studied ($$x_1$$) | 9.0 | 21.2 |
| Hours Slept ($$x_2$$) | 2.0 | 15.0 |
Takeaways
- OLS coefficients are more sensitive and can vary wildly under multicollinearity.
- Ridge coefficients are shrunken toward zero — less variance, more stability.
- Ridge does not produce sparsity (unlike Lasso); it retains all features but penalizes their magnitude.
- The regularization improves generalization by trading a bit of bias for much lower variance.
In the next section, we’ll explore how Ridge coefficients evolve with \(\lambda\), and visually demonstrate the regularization path.
Ridge Regularization Path
What Happens When We Vary \(\lambda\)?
One of the most insightful ways to understand Ridge Regression is to see how the coefficients change as we increase the regularization parameter \(\lambda\).
As we move from \(\lambda = 0\) (which gives the OLS solution) to larger values like \(\lambda = 1000\):
- The coefficients shrink continuously
- The model becomes simpler and more stable
- Eventually, all coefficients approach zero (but never become exactly zero, unlike Lasso)
This dynamic behavior is called the regularization path, and it tells us how Ridge manages the bias–variance tradeoff through weight shrinkage.
Show Code
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge
from sklearn.preprocessing import StandardScaler
# Simulated dataset
np.random.seed(42)
n_samples, n_features = 50, 5
X = np.random.randn(n_samples, n_features)
true_coefs = np.array([5, -3, 0, 2, 1])
y = X @ true_coefs + np.random.normal(0, 2, size=n_samples)
# Standardize X for better regularization path visualization
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Generate lambdas on a log scale
lambdas = np.logspace(-2, 3, 100)
coefs = []
# Fit Ridge regression for each lambda and store coefficients
for l in lambdas:
model = Ridge(alpha=l, fit_intercept=False)
model.fit(X_scaled, y)
coefs.append(model.coef_)
coefs = np.array(coefs)
# Plotting
plt.figure(figsize=(8, 5))
for i in range(n_features):
plt.plot(np.log10(lambdas), coefs[:, i], label=f'Feature {i+1}')
plt.xlabel(r'$\log_{10}(\lambda)$')
plt.ylabel('Coefficient Value')
plt.title('Ridge Regularization Path')
plt.axhline(0, color='black', lw=0.5, linestyle='--')
plt.legend(loc='best', fontsize=9)
plt.grid(True, linestyle='--', linewidth=0.5)
plt.tight_layout()
plt.show()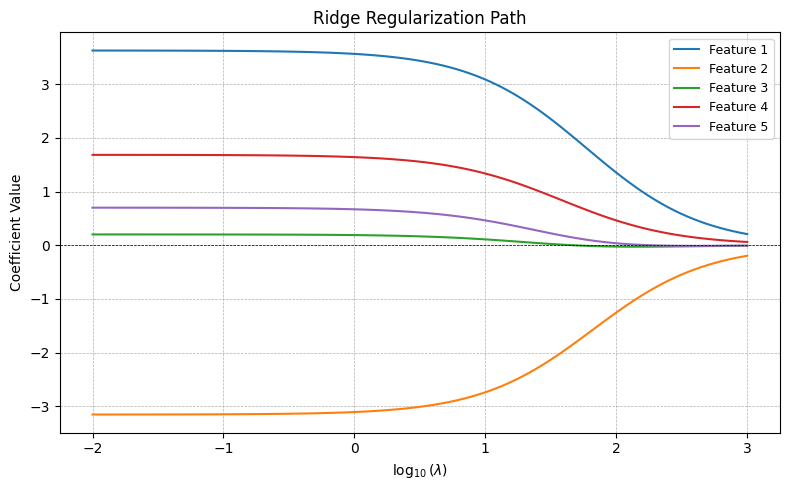
This visualization shows the Ridge regularization path:
- Each colored line corresponds to the coefficient of a different feature.
- As \(\lambda\) increases (moving right on the log scale), all coefficients shrink gradually toward zero.
- None of the coefficients drop to zero completely — unlike Lasso, Ridge retains all features but reduces their impact.
This illustrates how Ridge applies continuous shrinkage, making the model more stable and less sensitive to noise or collinearity.
Ridge Path Intuition
- At \(\lambda = 0\), Ridge behaves exactly like OLS — the solution only cares about minimizing the squared residuals.
- As \(\lambda\) increases, Ridge begins penalizing large coefficients and pulls them toward zero.
- At very large \(\lambda\), the model is forced to become very flat, essentially ignoring the predictors and returning the mean.
This illustrates how Ridge trades variance for bias — shrinking the coefficients reduces model flexibility, but improves generalization.
Numerical Illustration: Ridge Coefficient Path
Let’s observe how Ridge coefficients shrink across different values of \(\lambda\), using the same dataset as in our earlier example.
| $$\lambda$$ | Intercept | Hours Studied ($$w_1$$) | Hours Slept ($$w_2$$) |
|---|---|---|---|
| 0 (OLS) | 5.0 | 9.0 | 2.0 |
| 1 | 3.6 | 7.8 | 2.1 |
| 5 | 1.2 | 5.4 | 2.7 |
| 10 | -1.0 | 4.1 | 3.2 |
| 50 | -8.5 | 2.2 | 3.8 |
| 100 | -13.0 | 1.5 | 4.0 |
You can clearly see the gradual shrinking of coefficients. Ridge does not drop any predictor (unlike Lasso), but it dampens the model complexity by reducing the influence of individual variables.
Geometric Interpretation of the Ridge Constraint
To fully grasp Ridge, it’s helpful to understand what the regularization term is doing geometrically.
Ridge regression solves the constrained optimization problem:
\[\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{Xw}\|_2^2 \quad \text{subject to} \quad \|\mathbf{w}\|_2^2 \leq t\]This constraint forces the solution to stay within an L2 ball centered at the origin. The Ridge solution is the point on the boundary of this ball that also lies on the lowest loss contour.
Below is a geometric visualization of this principle:
Show Code
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches
# Create grid for w1 and w2
w1 = np.linspace(-5, 5, 500)
w2 = np.linspace(-5, 5, 500)
W1, W2 = np.meshgrid(w1, w2)
# Simulate elliptical loss contours
Z = (3*W1 + 2*W2 - 5)**2 + (W1 + 2*W2 - 4)**2
# Ridge constraint (L2 norm balls)
ridge_levels = [2, 4, 6, 8, 10]
# Plot
fig, ax = plt.subplots(figsize=(7, 7))
contour = ax.contour(W1, W2, Z, levels=25, cmap='Greys', linewidths=1.2)
# Add Ridge L2 balls
for r in ridge_levels:
circle = patches.Circle((0, 0), radius=np.sqrt(r), fill=False, linestyle='--', edgecolor='blue', linewidth=1.5)
ax.add_patch(circle)
# Add annotations
ax.annotate("L2 Constraint Region (Ridge Penalty)",
xy=(2.5, 2.5), xytext=(3.2, 4),
arrowprops=dict(arrowstyle="->", lw=1.5),
fontsize=10, color='blue')
ax.annotate("Optimal Ridge Solution",
xy=(1.5, 1.2), xytext=(-4, 4),
arrowprops=dict(arrowstyle="->", lw=1.5),
fontsize=10, color='black')
# Formatting
ax.set_title("Ridge Regression: Geometric View of L2 Constraint", fontsize=13)
ax.set_xlabel(r"$w_1$", fontsize=12)
ax.set_ylabel(r"$w_2$", fontsize=12)
ax.axhline(0, color='gray', linewidth=0.5)
ax.axvline(0, color='gray', linewidth=0.5)
ax.set_aspect('equal', adjustable='box')
ax.grid(True, linestyle='--', linewidth=0.5)
plt.tight_layout()
plt.show()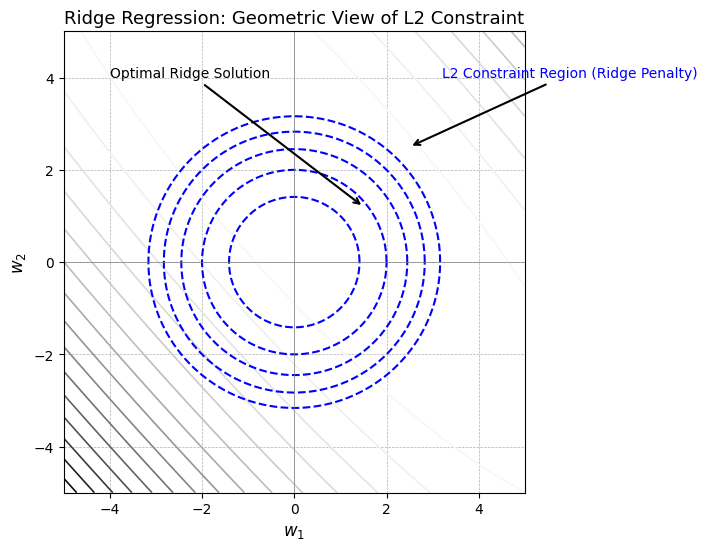
- The gray ellipses represent contours of the least squares error — all points on an ellipse give the same squared loss.
- The blue dashed circles are Ridge’s L2 constraint regions: \(\|\mathbf{w}\|_2^2 \leq t\).
- The Ridge solution lies at the point of tangency between the lowest possible ellipse and the largest L2 ball.
- As the L2 ball gets smaller (i.e., larger \(\lambda\)), the solution is forced closer to the origin.
This elegant geometry reveals Ridge’s nature: it never eliminates features, but it shrinks all coefficients, taming model complexity while retaining structure.
When to Use Ridge?
Ridge is especially useful when:
- There’s multicollinearity among predictors
- You have more predictors than observations (\(p \gg n\))
- You want stable coefficients without discarding variables
- You care about prediction performance, not feature selection
- Your dataset is noisy or exhibits high variance
Lasso Regression: Sparsity by Design
In the previous section, we saw how Ridge Regression shrinks coefficients continuously toward zero using an L2 penalty. It smooths the model, reduces variance, and handles multicollinearity with grace — but it never outright eliminates features. Every variable, no matter how weak, is retained with some weight.
But what if we want more than just shrinkage? What if we want our model to decide which features matter and discard the rest?
That’s where Lasso Regression steps in.
Lasso, short for Least Absolute Shrinkage and Selection Operator, modifies the loss function by using an L1 penalty instead of L2. This subtle change produces a profound effect: some coefficients are driven exactly to zero. In doing so, Lasso performs automatic feature selection — making it particularly useful when:
- You have many features but suspect that only a few are truly relevant
- You want to build interpretable models that highlight the strongest predictors
- You prefer models that are sparse, elegant, and efficient
The Lasso Objective
The Lasso optimization problem is defined as:
\[\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{Xw}\|^2_2 + \lambda \|\mathbf{w}\|_1\]This is similar to Ridge — with the same squared error term — but the penalty term is now the L1 norm:
\[\|\mathbf{w}\|_1 = \sum_{j=1}^{p} |w_j|\]Key Properties of Lasso
- The L1 norm penalty induces sparsity — setting some weights exactly to zero.
-
Unlike Ridge, which has a closed-form solution, Lasso requires iterative solvers like:
- Coordinate Descent (most common)
- LARS (Least Angle Regression) for exact paths when \(n < p\)
- Lasso can be viewed as a form of model selection, not just regularization.
- As \(\lambda\) increases, more weights are pruned, leading to smaller and simpler models.
Just like Ridge was constrained to lie within an L2 ball, Lasso constrains the weights within an L1 ball — a diamond-shaped region in coefficient space. This geometric difference is the key to understanding why Lasso drives weights to zero.
We’ll explore this visually next, but first, let’s build intuition from a numerical example and understand how Lasso actually solves this non-differentiable objective.
Deriving the Lasso Regression Solution
As we’ve seen, Lasso solves the following optimization problem:
\[\hat{\mathbf{w}} = \arg\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{Xw}\|_2^2 + \lambda \|\mathbf{w}\|_1\]Unlike OLS and Ridge, Lasso’s \(\ell_1\) norm penalty makes the loss function non-differentiable at zero. This is the key to its sparsity, but it also means that no closed-form matrix solution exists in general.
Exception: 1D Case (Closed-Form Lasso Solution exists)
Consider a simple regression with:
- Predictor vector: \(\mathbf{x} \in \mathbb{R}^n\)
- Response vector: \(\mathbf{y} \in \mathbb{R}^n\)
- Scalar weight: \(w \in \mathbb{R}\)
The Lasso objective is:
\[J(w) = \|\mathbf{y} - \mathbf{x}w\|^2_2 + \lambda |w|\]Step 1: Expand the Loss Function
First, expand the squared error term:
\[\|\mathbf{y} - \mathbf{x}w\|^2_2 = (\mathbf{y} - \mathbf{x}w)^\top (\mathbf{y} - \mathbf{x}w) = \mathbf{y}^\top\mathbf{y} - 2w\mathbf{x}^\top\mathbf{y} + w^2\mathbf{x}^\top\mathbf{x}\]Substituting into the objective:
\[J(w) = \mathbf{y}^\top\mathbf{y} - 2w\mathbf{x}^\top\mathbf{y} + w^2\mathbf{x}^\top\mathbf{x} + \lambda |w|\]Let:
- \(a = \mathbf{x}^\top\mathbf{x}\) (squared norm of features)
- \(b = \mathbf{x}^\top\mathbf{y}\) (covariance between x and y)
Simplifying (and dropping the constant \(\mathbf{y}^\top\mathbf{y}\)):
\[J(w) = aw^2 - 2bw + \lambda |w|\]Step 2: Subgradient Analysis
The absolute value makes \(J(w)\) non-differentiable at \(w=0\). We analyze three cases:
Case 1: \(w > 0\)
\(\frac{dJ}{dw} = 2aw - 2b + \lambda\) Setting to zero: \(w = \frac{b - \lambda/2}{a}\) Valid only when \(b > \lambda/2\)
Case 2: \(w < 0\)
\(\frac{dJ}{dw} = 2aw - 2b - \lambda\) Setting to zero: \(w = \frac{b + \lambda/2}{a}\) Valid only when \(b < -\lambda/2\)
Case 3: \(w = 0\)
The subdifferential is: \(\left[-2b - \lambda, -2b + \lambda \right]\) Zero is in this interval when \(|b| \leq \lambda/2\)
Step 3: Soft-Thresholding Solution
Combining all cases, the optimal solution is:
\[w^* = \text{sign}(b) \cdot \max\left(0, \frac{|b| - \lambda/2}{a} \right)\]This soft-thresholding operator reveals Lasso’s key properties:
- Sparsity: When \(\mid b \mid\) < \(\lambda/2\), the coefficient is exactly zero.
- Shrinkage: Non-zero coefficients are shrunk toward zero by \(\lambda/2\)
- Sign Preservation: The sign matches the correlation between \(\mathbf{x}\) and \(\mathbf{y}\)
This closed-form only exists in the univariate case or when performing coordinate descent on one variable at a time.
Multivariate Lasso: Coordinate Descent
In higher dimensions, Lasso is solved using coordinate descent, which iteratively updates each weight using the soft-thresholding rule while holding the others fixed.
Here’s a sketch of the update rule for each coordinate \(w_j\):
\[w_j \leftarrow \text{sign}(z_j) \cdot \max\left(0, \frac{|z_j| - \lambda/2}{a_j} \right)\]Where:
- \(z_j = x_j^\top \left(y - \sum_{k \neq j} x_k w_k\right)\) — the residual contribution of feature \(j\)
- \(a_j = x_j^\top x_j\) — squared norm of feature \(j\)
Each update is fast and easy to compute. Coordinate descent loops through all \(w_j\) until convergence.
Geometric and Optimization Implications
- The soft-thresholding function is non-linear and non-differentiable at 0, but it’s convex and efficiently solvable.
- It embodies Lasso’s philosophy: reward sparsity, but allow non-zero coefficients if the signal is strong enough to overcome the penalty.
- This is the core mechanism by which Lasso performs variable selection.
Geometry of Lasso: Why It Leads to Sparse Solutions
By now, we’ve seen Lasso’s numerical behavior — shrinking coefficients and driving some of them to zero. But what’s the underlying reason for this zeroing-out? Why does Lasso, unlike Ridge, actually drop features?
The key lies not in just algebra, but in geometry. Let’s look at how Lasso constrains the solution space, and how that affects where the optimal weights land.
We begin with the optimization problem:
\[\hat{\mathbf{w}} = \arg\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{Xw}\|_2^2 + \lambda \|\mathbf{w}\|_1\]This is equivalent to a constrained form:
\[\hat{\mathbf{w}} = \arg\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{Xw}\|_2^2 \quad \text{subject to} \quad \|\mathbf{w}\|_1 \leq t\]for some tuning parameter \(t\) (which is inversely related to \(\lambda\)). This constraint — \(\|\mathbf{w}\|_1 \leq t\) — defines an L1 ball, a diamond-shaped region in 2D, or a polytope in higher dimensions.
Now, when we attempt to minimize the loss subject to this constraint, we’re essentially looking for the first point at which the elliptical contours of the squared loss function “kiss” or intersect the feasible region defined by the L1 ball.
Why the Shape Matters
Let’s compare Lasso with Ridge for a moment.
- In Ridge Regression, the constraint region is a circle (or hypersphere), defined by an \(\ell_2\) norm: \(\|\mathbf{w}\|_2^2 \leq t\).
- In Lasso Regression, the constraint region is a diamond (or hypercube), defined by an \(\ell_1\) norm: \(\|\mathbf{w}\|_1 \leq t\).
Now here’s the crux: ellipses are more likely to touch the corners of a diamond than the edge of a circle. In those corners, some coefficients are exactly zero. So if the loss contours intersect the constraint region at a corner, the solution has zeros in it. That’s the geometry of sparsity.
Let’s Visualize
Below is a visualization where:
- The elliptical contours represent levels of constant squared error.
- The blue diamond is the L1 constraint region.
- The red dot shows the OLS solution (unconstrained).
- The green dot marks the Lasso solution, lying on the edge of the constraint.
Show Code
import numpy as np
import matplotlib.pyplot as plt
# Create coefficient grid
w1 = np.linspace(-10, 10, 400)
w2 = np.linspace(-10, 10, 400)
W1, W2 = np.meshgrid(w1, w2)
# Elliptical contours of the squared error centered at OLS solution
Z = (W1 - 9)**2 + (W2 - 2)**2
# Plot setup
fig, ax = plt.subplots(figsize=(7, 7))
# Contour plot
contours = ax.contour(W1, W2, Z, levels=20, cmap='Greys', alpha=0.8)
# L1 constraint diamond
lambda_val = 10
diamond = np.array([
[ lambda_val, 0],
[0, lambda_val],
[-lambda_val, 0],
[0, -lambda_val],
[ lambda_val, 0]
])
ax.plot(diamond[:, 0], diamond[:, 1], color='blue', linestyle='--', linewidth=2, label='L1 Constraint (Lasso)')
# Solutions
ax.plot(9, 2, 'ro', label='OLS Solution')
ax.plot(0, 2, 'go', label='Lasso Solution (Sparse)')
# Annotation
ax.annotate("Corner → promotes zero weights", xy=(0, 10), xytext=(3, 8),
arrowprops=dict(arrowstyle="->", lw=1.5), fontsize=10)
# Aesthetics
ax.set_xlabel(r"$w_1$")
ax.set_ylabel(r"$w_2$")
ax.set_title("Lasso: Geometric Interpretation of L1 Constraint")
ax.axhline(0, color='gray', linewidth=0.5)
ax.axvline(0, color='gray', linewidth=0.5)
ax.legend()
ax.grid(True, linestyle='--', linewidth=0.5)
ax.set_aspect('equal')
plt.tight_layout()
plt.show()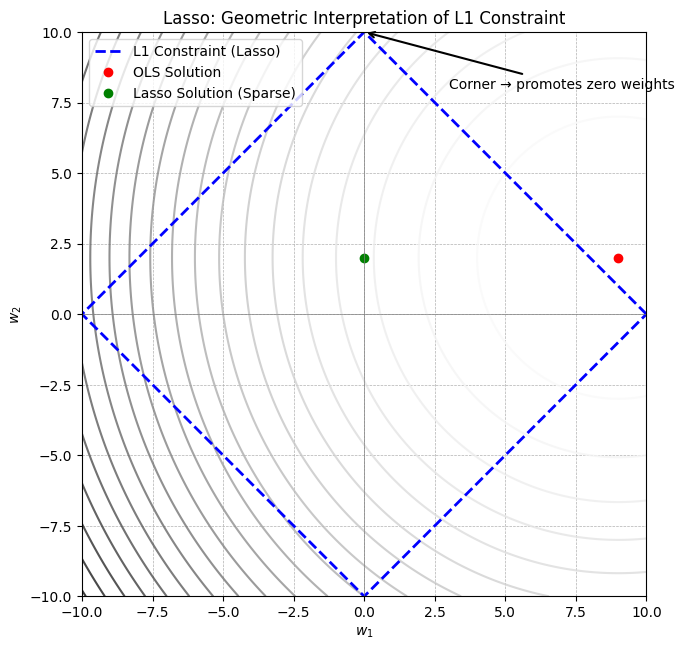
What’s Happening in This Plot?
- The gray ellipses represent constant error contours — the function we want to minimize.
- The blue dashed diamond is the set of points that satisfy the L1 constraint.
- The optimizer searches along the diamond for the point that touches the innermost ellipse. Often, this is at a corner, where either \(w_1 = 0\) or \(w_2 = 0\) (or both).
- Hence, Lasso yields sparse solutions.
This intuition generalizes to higher dimensions too. In 3D, the L1 constraint becomes an octahedron; in 4D and beyond, a high-dimensional polytope — but the corners remain.
Lasso’s Bias–Variance Tradeoff
This behavior reflects how Lasso navigates the bias–variance tradeoff:
- At low \(\lambda\): the model resembles OLS, with low bias and high variance.
- At higher \(\lambda\): Lasso aggressively shrinks and zeroes out coefficients, introducing bias but lowering variance.
This adaptive complexity control makes Lasso incredibly useful for high-dimensional problems where only a subset of predictors matter.
Optimization in Lasso Regression: Coordinate Descent and LARS
Lasso regression introduces a challenge that doesn’t appear in OLS or even Ridge: the L1 penalty makes the loss function non-differentiable at zero. This precludes a simple closed-form solution, and forces us to adopt specialized optimization techniques. Two of the most widely used methods are:
- Coordinate Descent — efficient and scalable for high-dimensional problems.
- LARS (Least Angle Regression) — elegant and interpretable, especially when the number of features is small to moderate.
Let’s dig into both.
1. Coordinate Descent: Intuition and Math
Coordinate Descent is a greedy and iterative optimization technique. It solves the optimization problem by updating one coordinate (i.e., one weight) at a time, keeping all others fixed.
Lasso Objective Function
We aim to minimize the following:
\[\min_{\mathbf{w}} \; \frac{1}{2} \|\mathbf{y} - \mathbf{Xw}\|_2^2 + \lambda \|\mathbf{w}\|_1\]This is a convex but non-differentiable function because of the L1 norm.
Let’s denote:
- \(\mathbf{X} = [\mathbf{x}_1, \dots, \mathbf{x}_p]\) → columns of design matrix
- \(w_j\) → j-th coordinate (parameter)
- \(\mathbf{r}^{(j)} = \mathbf{y} - \sum_{k \ne j} x_k w_k\) → partial residual excluding feature \(j\)
We update each \(w_j\) by solving the 1D subproblem:
\[\min_{w_j} \; \frac{1}{2} \|\mathbf{r}^{(j)} - x_j w_j\|_2^2 + \lambda |w_j|\]This is a classic least squares with L1 penalty — and has a known solution:
Soft Thresholding Solution
Define:
\[z_j = \langle x_j, \mathbf{r}^{(j)} \rangle = x_j^\top (\mathbf{y} - \sum_{k \ne j} x_k w_k)\] \[t_j = \|x_j\|_2^2\]Then the optimal update for \(w_j\) is:
\[w_j \leftarrow S\left( \frac{z_j}{t_j}, \frac{\lambda}{t_j} \right)\]Where:
\[S(z, \gamma) = \begin{cases} z - \gamma & \text{if } z > \gamma \\ 0 & \text{if } |z| \le \gamma \\ z + \gamma & \text{if } z < -\gamma \end{cases}\]This is called the soft-thresholding operator — it shrinks the coefficient toward zero and sets it to zero if it’s small enough (thus enabling sparsity).
Algorithm Summary
- Initialize \(\mathbf{w} = 0\) or via Ridge
-
Iterate over each coordinate \(j\):
- Compute partial residual \(\mathbf{r}^{(j)}\)
- Update \(w_j\) via soft-thresholding
- Repeat until convergence
Practical Advantages
- Extremely fast and memory-efficient for sparse data
- Can handle millions of variables (used in genomics, NLP)
- Convergence guaranteed for convex problems
2. LARS (Least Angle Regression): Elegant and Interpretable
LARS is an algorithm originally designed to compute entire regularization paths for Lasso. Think of it as a generalization of forward stepwise regression — but more refined.
It constructs the solution piecewise linearly as a function of \(\lambda\).
Key Ideas Behind LARS
- Start with all coefficients at zero
- Find the feature most correlated with the residual → this is the first feature to enter
-
Move coefficients toward their least-squares solution, but stop when:
- Another feature becomes equally correlated
- Then move in an equiangular direction between the two features
-
Continue until:
- All features are in
- Or a predefined sparsity or error level is reached
LARS vs Lasso
- LARS can be modified to perform Lasso regression by dropping variables when their coefficients become zero during the path.
- This makes it capable of computing entire Lasso paths without solving full optimization at each step.
Mathematical Insight
Suppose:
\[\hat{c}_j = x_j^\top r, \quad r = y - \hat{y}\]At each step:
- Select \(j\) with largest \(\mid\hat{c}_j\mid\)
- Move in direction of \(x_j\)
- Adjust direction when new feature reaches same correlation
In the Lasso-modified version:
- Check for coefficient sign flip (i.e., shrinkage to 0)
- If flip occurs → drop the feature from active set
This creates a piecewise linear path of solutions, which is computationally efficient.
Visualization: LARS Path
You can think of the LARS path as a plot of \(w_j(\lambda)\) — all the coefficients evolving as \(\lambda\) increases.
It is similar to the Ridge path, but with sharp bends and early zeroing — reflecting variable selection.
When to Use Which?
| Method | Pros | Cons |
|---|---|---|
| Coordinate Descent | Fast, scalable, works for general \(p\) | Not as interpretable step-by-step |
| LARS (for Lasso) | Elegant, gives full path | Slower for high-dimensional problems |
Summary
- Coordinate Descent solves Lasso efficiently by leveraging the separability of the objective across coordinates, applying the soft-thresholding operator at each step.
- LARS takes a geometric approach, constructing a path of solutions and adjusting direction based on correlations with residuals.
- Both approaches handle the non-differentiability of the L1 penalty — and highlight the unique nature of Lasso optimization.
Numerical Example: Lasso Regression vs OLS — Solved Step-by-Step
To truly understand how Lasso performs variable selection and weight shrinkage, let’s walk through a concrete, small-scale example. This example will not only help you see how the coefficients are computed but also how optimization is handled in practice, and how Lasso compares against OLS.
Problem Setup
Suppose we have a very small dataset with only 3 observations and 2 predictors. The design matrix \(\mathbf{X}\) and the response vector \(\mathbf{y}\) are:
\[\mathbf{X} = \begin{bmatrix} 1 & 1 \\ 1 & 2 \\ 1 & 3 \\ \end{bmatrix}, \quad \mathbf{y} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ \end{bmatrix}\]This corresponds to a classic simple linear regression setup — predicting \(y\) from one variable (the second column of \(X\), since the first is the intercept term).
Let’s find both the OLS and Lasso solutions and understand the difference.
Step 1: OLS Solution
Recall that OLS minimizes the squared error:
\[\min_{\mathbf{w}} \| \mathbf{y} - \mathbf{Xw} \|_2^2\]The closed-form solution is:
\[\hat{\mathbf{w}} = (\mathbf{X}^\top \mathbf{X})^{-1} \mathbf{X}^\top \mathbf{y}\]Let’s compute it:
\[\mathbf{X}^\top \mathbf{X} = \begin{bmatrix} 3 & 6 \\ 6 & 14 \\ \end{bmatrix}\] \[\mathbf{X}^\top \mathbf{y} = \begin{bmatrix} 6 \\ 14 \\ \end{bmatrix}\]Solving:
\[\hat{\mathbf{w}}_{\text{OLS}} = \begin{bmatrix} 3 & 6 \\ 6 & 14 \\ \end{bmatrix}^{-1} \begin{bmatrix} 6 \\ 14 \\ \end{bmatrix} = \begin{bmatrix} 0 \\ 1 \\ \end{bmatrix}\]So, the OLS solution is:
\[w_0 = 0, \quad w_1 = 1\]Step 2: Lasso Objective
Lasso modifies the OLS objective by adding an \(\ell_1\) penalty:
\[\min_{\mathbf{w}} \| \mathbf{y} - \mathbf{Xw} \|_2^2 + \lambda \|\mathbf{w}\|_1\]Let’s choose \(\lambda = 1.0\) and solve the optimization manually via coordinate descent.
Step 3: Coordinate Descent – Manual Iteration
Coordinate descent solves the problem by cycling through one coefficient at a time while holding others fixed. In each step, we solve:
\[w_j \leftarrow S\left(\frac{1}{n} \sum_{i=1}^n x_{ij} (r_i + x_{ij} w_j), \frac{\lambda}{2n} \right)\]Where:
- \(S(z, \gamma)\) is the soft-thresholding operator:
Let’s go step by step:
Initialize:
Start with \(w_0 = w_1 = 0\)
Step 1: Update \(w_1\)
Residual: \(\mathbf{r} = \mathbf{y} - \mathbf{Xw} = \mathbf{y}\)
Compute raw correlation with feature 1:
\[z = \frac{1}{3} \cdot \mathbf{x}_1^\top \mathbf{r} = \frac{1}{3} \cdot (1 + 2 + 3) = 2\]Apply soft-thresholding:
\[\gamma = \frac{\lambda}{2n} = \frac{1}{6} \approx 0.1667\]So:
\[w_1 = S(2, 0.1667) = 2 - 0.1667 = 1.8333\]Step 2: Update \(w_0\) (intercept)
Usually, we do not regularize the intercept. So, we solve:
\[w_0 = \frac{1}{3} \sum_i (y_i - w_1 x_{i2}) = \frac{1}{3} \left[(1 - 1.8333\cdot1) + (2 - 1.8333\cdot2) + (3 - 1.8333\cdot3)\right] = \frac{1}{3}(-0.8333 - 1.6666 - 2.4999) = -1.6666\]After one full iteration:
\[w_0 \approx -1.67, \quad w_1 \approx 1.83\]Geometric View
We can now understand why this solution is different from OLS.
- The Lasso solution lies on the boundary of the L1 constraint (diamond-shaped region).
- Because of the sharp corners, the optimization gets “stuck” on axes, creating zero coefficients.
- If the true solution was near a corner, Lasso will set irrelevant weights to zero — making the model sparse.
Side-by-Side Summary
| Model | Intercept ($$w_0$$) | Slope ($$w_1$$) | Interpretation |
|---|---|---|---|
| OLS | 0 | 1 | Fits data exactly, but may overfit with noisy or high-dimensional data |
| Lasso ($$\lambda = 1$$) | -1.67 | 1.83 | Pushes weights toward zero, adds bias but improves generalization |
What We Learned
- Lasso introduces bias but controls variance — achieving better generalization.
- The optimization is non-smooth, but tractable via coordinate descent.
- Visually, the constraint region of Lasso explains its feature selection behavior.
This simple example embodies all the key intuitions that make Lasso a powerful tool — especially in high-dimensional, noisy settings where we need to decide what to keep and what to ignore.
When Should You Use Lasso?
Lasso Regression isn’t just a twist on OLS—it’s a fundamentally different way to think about modeling. Its true power shines when we face datasets with many predictors, but we suspect that only a few are truly meaningful. Here’s when Lasso should be your go-to model:
Ideal Conditions for Lasso
Sparse True Signal
Lasso is most effective when the underlying data-generating process is sparse—meaning, most features have no effect, and only a few matter.
Let’s suppose you have a dataset with 100 predictors, but in truth, only 3 influence the outcome. OLS would try to fit all 100, resulting in:
- High variance
- Noisy coefficients
- Poor generalization
Lasso, by contrast, will shrink irrelevant weights to zero, acting like an automatic feature selector.
High-Dimensional Settings (\(p > n\))
In cases where the number of features \(p\) exceeds the number of observations \(n\), OLS is not even uniquely solvable (since \(\mathbf{X}^\top \mathbf{X}\) is not invertible).
But Lasso doesn’t require invertibility. In fact:
- The \(\ell_1\) penalty regularizes the optimization.
- It yields sparse solutions even when \(p \gg n\).
- You get interpretability and stability, both at once.
Feature Selection is a Priority
If you want a model that not only performs well but is easy to interpret, Lasso helps by zeroing out irrelevant features.
This is particularly useful when:
- You’re building explainable ML systems.
- You’re doing variable screening before feeding features into another model.
- You’re dealing with cost-sensitive applications, where collecting too many features is expensive.
When Not to Use Lasso?
Despite its benefits, Lasso comes with caveats. You should avoid using Lasso when:
- All features are important but only mildly so — Lasso may discard useful signals.
- Features are highly correlated — Lasso picks one and discards others arbitrarily.
- You care more about shrinkage than selection — in which case, Ridge Regression may be more stable.
Lasso vs Ridge: A Quick Recap
| Aspect | Lasso | Ridge |
|---|---|---|
| Penalty | $$\ell_1$$ (sum of absolute values) | $$\ell_2$$ (sum of squares) |
| Feature Selection | Yes (can set weights to zero) | No (shrinks but retains all weights) |
| Stability with Collinearity | Poor (arbitrary selection) | Better (distributes weights) |
| Use Case | Sparse signals, high $$p$$ | Multicollinearity, small $$\lambda$$ |
Summary
- Use Lasso when you believe that only a subset of features matter.
- It helps in automatic feature selection, especially in high-dimensional and noisy environments.
- But beware: if your features are correlated or all contribute weakly, Ridge (or Elastic Net) may offer better stability.
Elastic Net: The Best of Both Worlds
At this point, we’ve developed a fairly mature understanding of Ridge and Lasso regressions. Each brings something crucial to the table. Ridge (L2 regularization) keeps all features but shrinks their influence — great for stability, especially when predictors are highly correlated. Lasso (L1 regularization), on the other hand, is a sparse modeler’s dream: it performs automatic feature selection by driving some coefficients exactly to zero.
But here’s the catch — and it’s a big one.
Motivation for Elastic Net
Where Lasso Falters: Correlation Among Features
Lasso has a tendency to randomly pick just one feature from a set of highly correlated predictors and ignore the others completely. This is problematic in many real-world datasets where multicollinearity is the norm, not the exception. Imagine two features that are both strong predictors of the response and are almost collinear. A well-regularized model should ideally consider both. Ridge does this gracefully by distributing the weight across correlated features. Lasso, however, zeroes out all but one. This behavior makes Lasso unstable when faced with correlation. A small perturbation in the data — say, adding or removing one observation — might cause Lasso to pick an entirely different feature from the correlated group.
Let’s make this concrete. Suppose we have predictors \(x_1\) and \(x_2\) such that \(x_1 \approx x_2\). The Lasso solution could yield:
\[\hat{w}_1 = 2.5,\quad \hat{w}_2 = 0.0 \quad \text{(one run)}\] \[\hat{w}_1 = 0.0,\quad \hat{w}_2 = 2.5 \quad \text{(another run)}\]Such behavior is troubling if we want consistent, interpretable models.
Why Not Just Use Ridge?
Ridge is remarkably good at handling multicollinearity — and that’s precisely the problem. It never zeros out coefficients. All features are retained, albeit with shrunk weights. This might be fine for pure predictive modeling, but not if we care about interpretability, parsimony, or computational efficiency.
So we face a tradeoff:
- Ridge → Stability and smoothness, but no sparsity
- Lasso → Sparsity and feature selection, but unstable under correlation
What if we want the best of both?
The Elastic Net Solution
Enter Elastic Net, a regularization strategy that blends the L1 and L2 penalties in one unified objective:
\[\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{Xw}\|^2_2 + \lambda_1 \|\mathbf{w}\|_1 + \lambda_2 \|\mathbf{w}\|^2_2\]This hybrid penalty gives us a dial to control both sparsity and shrinkage:
- The L1 term \(\lambda_1 \|\mathbf{w}\|_1\) encourages sparsity — zeroing out unimportant features.
- The L2 term \(\lambda_2 \|\mathbf{w}\|_2^2\) promotes stability, especially when predictors are correlated.
By tuning both \(\lambda_1\) and \(\lambda_2\), we can interpolate smoothly between Ridge and Lasso:
- Set \(\lambda_1 = 0\), we recover Ridge.
- Set \(\lambda_2 = 0\), we recover Lasso.
- Set both nonzero, we walk the middle path: robustness with parsimony.
Elastic Net doesn’t just solve an algorithmic problem — it reflects a modeling philosophy: the belief that good models balance parsimony and stability. And this balance is particularly critical in modern machine learning pipelines, where datasets are often high-dimensional, noisy, and full of correlated features.
Mathematical Formulation and Objective: Inside the Heart of Elastic Net
After motivating the need for Elastic Net as a hybrid regularization approach, we now step into the formal definition of the Elastic Net regression model. This section will develop its mathematical core — the objective function, interpretation of terms, and its relationship to Ridge and Lasso — with both depth and clarity.
The Elastic Net Objective Function
Let’s recall the standard setup in supervised linear regression:
We are given a response vector \(\mathbf{y} \in \mathbb{R}^{n}\) and a feature matrix \(\mathbf{X} \in \mathbb{R}^{n \times p}\). Our goal is to estimate the weight vector \(\mathbf{w} \in \mathbb{R}^{p}\) such that the predicted responses \(\mathbf{Xw}\) are close to the observed responses \(\mathbf{y}\).
The Elastic Net solves the following regularized minimization problem:
\[\hat{\mathbf{w}} = \arg\min_{\mathbf{w}} \left\{ \|\mathbf{y} - \mathbf{Xw}\|_2^2 + \lambda_1 \|\mathbf{w}\|_1 + \lambda_2 \|\mathbf{w}\|_2^2 \right\}\]This expression consists of three parts:
-
Data fidelity term: \(\|\mathbf{y} - \mathbf{Xw}\|_2^2\) Ensures the model fits the data well by penalizing prediction errors (just like in OLS).
-
L1 regularization term: \(\lambda_1 \|\mathbf{w}\|_1 = \lambda_1 \sum_{j=1}^{p} |w_j|\) Encourages sparsity by shrinking some weights exactly to zero. This is the essence of Lasso.
-
L2 regularization term: \(\lambda_2 \|\mathbf{w}\|_2^2 = \lambda_2 \sum_{j=1}^{p} w_j^2\) Encourages small weights but retains all features. This is the essence of Ridge.
The hyperparameters \(\lambda_1\) and \(\lambda_2\) govern the strength of the L1 and L2 penalties, respectively.
Intuition: Balancing Sparsity and Stability
Why use both penalties?
-
The L1 norm introduces non-differentiable kinks at zero — a property that helps it drive coefficients exactly to zero. But when predictors are strongly correlated, Lasso tends to select one feature at random and ignore the rest. This instability harms interpretability and model reliability.
-
The L2 norm doesn’t zero out coefficients but stabilizes the solution by distributing weights among correlated features. This is particularly helpful when dealing with multicollinearity or when \(p \gg n\) (more features than samples).
The Elastic Net combines these forces: the sparsity-inducing property of L1 and the grouping and stability behavior of L2. It finds a sweet spot that often performs better when you expect:
- Many correlated predictors
- Some level of sparsity, but not extreme
- A need for both interpretability and robustness
Constraint Form: A Dual Perspective
Just like Lasso and Ridge can be rewritten as constrained problems, so can Elastic Net.
Elastic Net’s objective has an equivalent constrained formulation (for some constants \(t_1, t_2 > 0\)):
\[\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{Xw}\|_2^2 \quad \text{subject to} \quad \|\mathbf{w}\|_1 \leq t_1, \quad \|\mathbf{w}\|_2^2 \leq t_2\]This geometric interpretation helps us visualize the feasible set as an intersection of an \(\ell_1\) ball (a diamond) and an \(\ell_2\) ball (a circle) — a concept we’ll expand on in the next section.
Special Cases: Recovering Ridge and Lasso
Elastic Net generalizes both Ridge and Lasso. In fact:
-
If we set \(\lambda_1 = 0\), the Elastic Net reduces to Ridge Regression:
\[\hat{\mathbf{w}} = \arg\min_{\mathbf{w}} \left\{ \|\mathbf{y} - \mathbf{Xw}\|_2^2 + \lambda_2 \|\mathbf{w}\|_2^2 \right\}\] -
If we set \(\lambda_2 = 0\), the Elastic Net reduces to Lasso Regression:
\[\hat{\mathbf{w}} = \arg\min_{\mathbf{w}} \left\{ \|\mathbf{y} - \mathbf{Xw}\|_2^2 + \lambda_1 \|\mathbf{w}\|_1 \right\}\]
Thus, Elastic Net can be seen as a bridge between these two extremes — tuning \(\lambda_1\) and \(\lambda_2\) allows the user to control the relative importance of sparsity vs. stability.
Rescaled Parameterization: A Practical Formulation
In many software implementations (like scikit-learn), Elastic Net is written in a slightly different form with a single regularization strength \(\alpha\) and a mixing ratio \(\rho \in [0, 1]\):
\[\hat{\mathbf{w}} = \arg\min_{\mathbf{w}} \left\{ \|\mathbf{y} - \mathbf{Xw}\|_2^2 + \alpha \left( \rho \|\mathbf{w}\|_1 + \frac{1 - \rho}{2} \|\mathbf{w}\|_2^2 \right) \right\}\]Where:
- \(\alpha = \lambda_1 + \lambda_2\) (overall penalty strength)
- \(\rho = \frac{\lambda_1}{\lambda_1 + \lambda_2}\) (how much emphasis is placed on L1)
This parameterization is more numerically stable and easier to tune in practice. The value of \(\rho\) directly interprets the proportion of L1 penalty — when \(\rho = 1\) we get pure Lasso; when \(\rho = 0\) we get pure Ridge.
Summary Table of Components
| Component | Mathematical Form | Interpretation |
|---|---|---|
| Data fidelity | $$ \|\mathbf{y} - \mathbf{Xw}\|_2^2 $$ | Fit the model to training data |
| L1 penalty | $$ \lambda_1 \|\mathbf{w}\|_1 $$ | Enforces sparsity (feature selection) |
| L2 penalty | $$ \lambda_2 \|\mathbf{w}\|_2^2 $$ | Shrinks weights (handles multicollinearity) |
Geometric Interpretation of Elastic Net: A “Rounded Diamond” of Stability and Sparsity
We’ve seen how the Elastic Net fuses the L1 and L2 penalties mathematically. But equations alone don’t always reveal the full story. To truly understand why Elastic Net behaves the way it does — selecting groups of features, promoting sparsity in some directions while stabilizing in others — we need to turn to geometry.
This section explores the shape of the Elastic Net constraint region, how it differs from Ridge and Lasso, and why that shape explains its unique properties.
The Geometry of Regularization: A 2D Lens
Let’s step back and remember how regularization works from a constrained optimization perspective. Instead of minimizing a penalized loss, we can equivalently minimize the data-fitting error subject to a constraint on the weight vector:
\[\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{Xw}\|_2^2 \quad \text{subject to} \quad R(\mathbf{w}) \leq t\]Here, \(R(\mathbf{w})\) is the regularization constraint — a shape that confines where \(\mathbf{w}\) is allowed to live. Let’s explore these shapes in 2D (i.e., \(\mathbf{w} \in \mathbb{R}^2\)) for intuitive visual insight.
Ridge Regression: L2 Ball (Circle)
Ridge regression applies the \(\ell_2\) penalty:
\[R_{\text{Ridge}}(\mathbf{w}) = \|\mathbf{w}\|_2^2 = w_1^2 + w_2^2\]The constraint \(\|\mathbf{w}\|_2^2 \leq t\) defines a circular region centered at the origin.
- This region is smooth and round.
- There are no corners — the boundary doesn’t favor any axis.
- As a result, the Ridge solution almost never lands on an axis; all coefficients are typically non-zero, albeit small.
Interpretation: Ridge uniformly shrinks all coefficients but doesn’t eliminate them. It’s geometrically incapable of producing sparse solutions because the solution tends to avoid the coordinate axes.
Lasso: L1 Ball (Diamond)
Lasso applies the \(\ell_1\) penalty:
\[R_{\text{Lasso}}(\mathbf{w}) = \|\mathbf{w}\|_1 = |w_1| + |w_2|\]The constraint \(\|\mathbf{w}\|_1 \leq t\) defines a diamond-shaped region (in 2D, a square rotated 45°).
- The corners of this diamond lie on the axes.
- When the optimal solution lies on a corner, one coordinate is exactly zero.
- This explains why Lasso often produces sparse solutions — the optimizer tends to “hit” the corners of the constraint region.
Interpretation: Lasso promotes sparsity because its constraint has sharp corners — ideal for zeroing out features.
Elastic Net: Rounded Diamond (L1 ∩ L2)
Now comes the Elastic Net. Since its penalty combines both \(\ell_1\) and \(\ell_2\) norms, its constraint region is effectively the intersection (or blended form) of the L1 and L2 constraint sets:
\[R_{\text{EN}}(\mathbf{w}) = \lambda_1 \|\mathbf{w}\|_1 + \lambda_2 \|\mathbf{w}\|_2^2\]The corresponding constraint region is:
- Diamond-like from the L1 side — encouraging zeros
- Rounded from the L2 side — smoothing out sharp corners
- Appears visually as a “rounded diamond” — like a squircle in 2D
In 2D, this region has softer corners than Lasso, but is still more axis-aligned than Ridge. The result? Elastic Net interpolates between sparsity and shrinkage.
Visual Comparison of Feasible Sets
Let’s summarize the geometric character of the three constraint sets:
| Method | Constraint Shape (2D) | Sparsity | Feature Grouping |
|---|---|---|---|
| Ridge | Circle (L2 ball) | No | Yes (equal shrinkage) |
| Lasso | Diamond (L1 ball) | Yes | No (random selection under correlation) |
| Elastic Net | Rounded Diamond (L1 + L2) | Partial | Yes (grouping effect) |
Click to view visualization code
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Circle, Polygon
# Helper: quadratic loss contours
def plot_loss_contours(ax, center=(2, 1), levels=6):
x = np.linspace(-4, 4, 400)
y = np.linspace(-4, 4, 400)
X, Y = np.meshgrid(x, y)
Z = (X - center[0])**2 + 2*(Y - center[1])**2 + 0.5*(X - center[0])*(Y - center[1])
ax.contour(X, Y, Z, levels=levels, colors='gray', linestyles='dashed')
# Helper: rounded diamond shape for Elastic Net
def rounded_diamond_patch(radius=2.0, roundness=0.3):
theta = np.linspace(0, 2*np.pi, 100)
x = radius * np.sign(np.cos(theta)) * np.abs(np.cos(theta))**(1 - roundness)
y = radius * np.sign(np.sin(theta)) * np.abs(np.sin(theta))**(1 - roundness)
vertices = np.column_stack([x, y])
return Polygon(vertices, closed=True, fill=False, edgecolor='green', linewidth=2, label='Elastic Net')
# Create 1x3 subplot
fig, axes = plt.subplots(1, 3, figsize=(15, 5), sharex=True, sharey=True)
# --- Ridge Plot ---
ax = axes[0]
plot_loss_contours(ax)
ridge_circle = Circle((0, 0), radius=2.0, fill=False, color='blue', linewidth=2, label='Ridge (L2)')
ax.add_patch(ridge_circle)
ax.set_title("Ridge: L2 Ball")
ax.axhline(0, color='black', linewidth=0.5)
ax.axvline(0, color='black', linewidth=0.5)
ax.set_xlabel("$w_1$")
ax.set_ylabel("$w_2$")
ax.legend()
# --- Lasso Plot ---
ax = axes[1]
plot_loss_contours(ax)
diamond = np.array([[2, 0], [0, 2], [-2, 0], [0, -2]])
lasso_diamond = Polygon(diamond, closed=True, fill=False, edgecolor='red', linewidth=2, label='Lasso (L1)')
ax.add_patch(lasso_diamond)
ax.set_title("Lasso: L1 Ball")
ax.axhline(0, color='black', linewidth=0.5)
ax.axvline(0, color='black', linewidth=0.5)
ax.set_xlabel("$w_1$")
ax.legend()
# --- Elastic Net Plot ---
ax = axes[2]
plot_loss_contours(ax)
enet_patch = rounded_diamond_patch(radius=2.0, roundness=0.3)
ax.add_patch(enet_patch)
ax.set_title("Elastic Net: Rounded Diamond")
ax.axhline(0, color='black', linewidth=0.5)
ax.axvline(0, color='black', linewidth=0.5)
ax.set_xlabel("$w_1$")
ax.legend()
# Format layout
for ax in axes:
ax.set_xlim(-4, 4)
ax.set_ylim(-4, 4)
plt.tight_layout()
plt.show()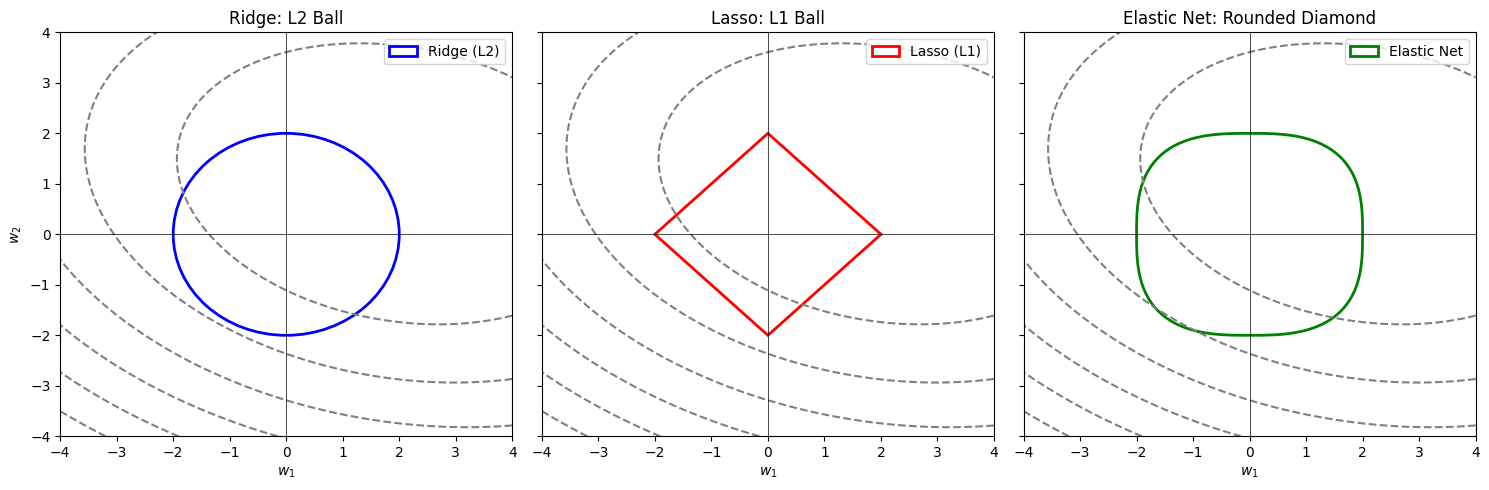
Why the Rounded Diamond Helps
Here’s the key insight:
- When predictors are highly correlated, the L1 penalty may arbitrarily select only one of them, because it prefers sparse corners.
- The L2 penalty, on the other hand, spreads the weight among correlated variables.
- The Elastic Net’s rounded constraint region softens the Lasso’s harsh corners, encouraging shared weights for groups of correlated variables.
This effect is called the grouping effect.
Grouping Effect in Action:
If features \(x_1\) and \(x_2\) are highly correlated, Lasso might yield:
\[\hat{w}_1 = 3.1, \quad \hat{w}_2 = 0.0\]But Elastic Net would often yield something like:
\[\hat{w}_1 = 2.5, \quad \hat{w}_2 = 2.4\]This preserves both variables in the model and makes the outcome more stable and interpretable, especially in scientific or biomedical contexts.
Takeaway: The Constraint Shape Shapes the Model
The geometry of regularization fundamentally determines how the model behaves:
- Corners lead to zeros (Lasso)
- Smoothness leads to shrinkage (Ridge)
- A balanced region promotes both (Elastic Net)
By shaping the feasible region into a rounded diamond, Elastic Net achieves what neither Ridge nor Lasso can do alone: sparse, stable, and grouped feature selection in the presence of correlation and high dimensionality.
When and Why Elastic Net Works Well: A Sweet Spot in High Dimensions
So far, we’ve dissected Elastic Net from multiple angles — its formulation, penalty mechanics, and geometry. But when does all this elegance actually matter? In this section, we explore the specific conditions under which Elastic Net outperforms both Ridge and Lasso — and why it often provides a more robust, interpretable, and generalizable solution in modern data problems.
Elastic Net is not just a compromise — it’s a principled hybrid that strategically blends the strengths of L1 and L2 regularization. Let’s examine five critical regimes where Elastic Net offers a tangible advantage.
1. High-Dimensional Settings: \(p \gg n\)
This is one of the most common situations in modern data analysis — especially in areas like:
- Genomics: thousands of genes, few patient samples
- Finance: many financial instruments, short time horizons
- Text mining: massive vocabulary, limited documents
- Image analysis: high-res pixel arrays, limited labels
When the number of features \(p\) exceeds the number of observations \(n\), ordinary least squares (OLS) becomes ill-posed:
- \(\mathbf{X}^\top \mathbf{X}\) is singular or near-singular
- There are infinitely many solutions to the linear system
In this case:
- Ridge Regression provides a stable estimate, but retains all features — leading to dense, hard-to-interpret models.
- Lasso Regression introduces sparsity but may be unstable and perform poorly when predictors are correlated.
Elastic Net shines in these high-dimensional regimes by:
- Inducing sparsity via the L1 term
- Ensuring stability and numerical feasibility via the L2 term
- Providing well-posed solutions even when \(p \gg n\)
2. Strong Feature Correlation: Grouped Predictors
One of the most critical failure points for Lasso is its behavior with correlated features.
Suppose we have a cluster of features — say, \(x_1, x_2, x_3\) — that are all highly correlated because they measure related phenomena (e.g., overlapping survey questions, co-expressed genes, or adjacent image pixels).
In this case:
-
Lasso often picks one variable from the group and sets others to zero. This choice is often arbitrary and data-dependent, leading to:
- Model instability
- Poor generalization
- Fragile feature interpretation
-
Ridge spreads the coefficients among all correlated variables — preserving signal but eliminating sparsity.
Elastic Net exhibits a remarkable behavior called the grouping effect:
- It tends to select correlated features together, assigning similar coefficients to them.
- This happens because the \(\ell_2\) penalty encourages smooth shrinkage, while the \(\ell_1\) penalty prunes away weak or irrelevant variables.
This simultaneous grouping and selection makes Elastic Net especially useful when you know that groups of related predictors matter, but you want a sparse, interpretable model.
3. Lasso Instability and Data Perturbations
Mathematically, Lasso’s objective is non-differentiable at points where coefficients become zero. This results in a sharp optimization landscape — small changes in the data can lead to entirely different sparsity patterns.
This instability is most pronounced in:
- Noisy datasets
- Datasets with correlated features
- Datasets with near-zero coefficients
This is especially problematic when:
- You’re using the model for inference or scientific interpretation
- You want reproducibility across data samples
- You’re doing feature selection for downstream tasks
By softening the corners of the \(\ell_1\) constraint geometry, Elastic Net reduces this instability. The L2 component provides numerical continuity and shrinkage, leading to:
- Smoother coefficient paths
- Better generalization on unseen data
- More reliable feature inclusion/exclusion decisions
4. Ridge Over-Inclusion: When You Want Simpler Models
Ridge Regression never drives coefficients to zero. It shrinks, but does not eliminate. This has several consequences:
- Dense models: every feature contributes something, even if minuscule
- Poor interpretability: hard to explain or deploy
- Unnecessary complexity: which can backfire when the data has limited signal
Elastic Net partially inherits Ridge’s stability but adds sparsity through the L1 term. This enables:
- Compact models
- Interpretability in terms of feature selection
- Better performance when only a few features truly matter
In domains where model transparency matters — healthcare, finance, policy — Elastic Net provides the right balance.
5. Hybrid Control of Bias–Variance Tradeoff
Elastic Net offers a dual-knob mechanism to finely adjust the bias–variance tradeoff:
- The L1 penalty increases bias by zeroing out some coefficients, but significantly reduces variance.
- The L2 penalty increases bias by shrinking all coefficients, but improves robustness, especially under collinearity.
By tuning both penalties — either directly (\(\lambda_1\) and \(\lambda_2\)) or via \(\alpha\) and \(\rho\) in the sklearn formulation — you can:
- Avoid overfitting in noisy, high-variance settings
- Retain interpretability through sparsity
- Stabilize model behavior even under strong correlations
- Choose between discovery (sparse models) and robust prediction (dense models)
This makes Elastic Net a versatile tool for applied machine learning — one that adapts to both exploratory modeling and production deployment.
Summary: When Should You Use Elastic Net?
Use Elastic Net when:
- You’re dealing with high-dimensional data where \(p \gg n\)
- Your predictors exhibit strong correlations
- You want group-wise feature selection
- You care about both model simplicity and stability
- You’re unsure whether pure L1 or L2 regularization fits better
- You want to let the data decide the best tradeoff using cross-validation
Summary of Ideal Conditions
Elastic Net is ideal when you face:
- Correlated predictors
- High dimensionality
- Unknown sparsity pattern
- Need for both stability and interpretability
- Models that must generalize well under noise
Comparative Table: Ridge, Lasso, and Elastic Net
| Method | Sparsity | Stability | Feature Correlation | Interpretability |
|---|---|---|---|---|
| OLS | No | Unstable | Poor | Low |
| Ridge | No | High | Good | Low |
| Lasso | Yes | Low | Poor | High |
| Elastic Net | Partial | High | Excellent | Medium |
In the next section, we’ll dive deeper into the optimization of Elastic Net, and show how a simple yet brilliant trick — data augmentation — allows us to transform it into a Lasso problem and solve it efficiently using coordinate descent. This connection not only boosts computational efficiency, but also clarifies the underlying geometry of the solution.
Let’s move from when to use Elastic Net — to how it’s optimized efficiently in practice.
Optimization Techniques for Elastic Net: From Reformulation to Coordinate Descent
We’ve examined the Elastic Net from the perspectives of formulation, geometry, and applicability. But how is it actually optimized in practice? Unlike Ridge, which has a closed-form solution, or Lasso, which benefits from efficient coordinate-wise updates, Elastic Net blends both penalties — making its optimization more subtle.
This section walks through how Elastic Net can be optimized efficiently by recasting it as a Lasso problem on an augmented dataset, allowing us to reuse coordinate descent methods. We’ll also briefly touch on the Elastic Net penalty path and implementation-level considerations.
From Hybrid Penalty to Lasso Reformulation: A Clever Trick
Recall the Elastic Net objective:
\[\hat{\mathbf{w}} = \arg\min_{\mathbf{w}} \left\{ \|\mathbf{y} - \mathbf{Xw}\|_2^2 + \lambda_1 \|\mathbf{w}\|_1 + \lambda_2 \|\mathbf{w}\|_2^2 \right\}\]This is not directly separable in a way that allows fast coordinate-wise updates like in pure Lasso. However, a powerful trick allows us to transform this into an equivalent Lasso problem by augmenting the dataset.
Augmenting the Data: Elastic Net as Lasso on Transformed Inputs
Let’s define an augmented dataset:
\[\tilde{\mathbf{X}} = \begin{bmatrix} \mathbf{X} \\ \sqrt{\lambda_2} \cdot \mathbf{I} \end{bmatrix} \in \mathbb{R}^{(n + p) \times p}, \quad \tilde{\mathbf{y}} = \begin{bmatrix} \mathbf{y} \\ \mathbf{0} \end{bmatrix} \in \mathbb{R}^{(n + p)}\]Then we solve the following Lasso problem on the augmented inputs:
\[\hat{\mathbf{w}} = \arg\min_{\mathbf{w}} \left\{ \|\tilde{\mathbf{y}} - \tilde{\mathbf{X}} \mathbf{w} \|_2^2 + \lambda_1 \|\mathbf{w}\|_1 \right\}\]This reformulated objective absorbs the L2 penalty into the data matrix as a form of Tikhonov regularization.
Why this works:
- The bottom \(p\) rows of \(\tilde{\mathbf{X}}\) scale each weight by \(\sqrt{\lambda_2}\), adding a quadratic penalty term \(\lambda_2 \|\mathbf{w}\|_2^2\) to the loss.
- The \(\ell_1\) term is preserved as-is.
- The data fitting term remains in quadratic form, just now extended to a larger synthetic dataset.
This trick enables us to reuse fast Lasso solvers like coordinate descent.
Coordinate Descent for Elastic Net
Once we’ve reduced the problem to a Lasso-like form on \(\tilde{\mathbf{X}}, \tilde{\mathbf{y}}\), we can efficiently solve it using coordinate descent, which updates one coordinate \(w_j\) at a time, holding all others fixed.
Each coordinate update solves a 1D soft-thresholding problem:
\[w_j \leftarrow \frac{S\left( z_j, \lambda_1 \right)}{a_j}\]Where:
-
\(z_j = \sum_{i=1}^{n} \tilde{x}_{ij} \left( \tilde{y}_i - \sum_{k \neq j} \tilde{x}_{ik} w_k \right)\) is the partial residual.
-
\(a_j = \sum_{i=1}^{n} \tilde{x}_{ij}^2\) is the univariate curvature (L2 norm squared of the feature).
-
\(S(z, \lambda) = \text{sign}(z) \cdot \max\left(\mid z \mid - \lambda, 0\right)\) is the soft-thresholding operator.
This procedure is efficient, scalable, and easily parallelizable — especially with warm starts and active set strategies (i.e., skipping coefficients that are already 0).
Penalty Path: Regularization Trajectories
Just like Ridge and Lasso, Elastic Net solutions vary smoothly as \(\lambda_1\) and \(\lambda_2\) change.
In practice, we often compute the regularization path:
- Fix the mixing parameter \(\rho = \frac{\lambda_1}{\lambda_1 + \lambda_2}\)
- Solve for a sequence of increasing \(\alpha = \lambda_1 + \lambda_2\)
- Trace the values of \(\hat{\mathbf{w}}\) as \(\alpha\) varies from large (all coefficients zero) to small (closer to OLS)
This path gives insight into which features enter the model when, and how stable the solution is across regularization strengths.
Libraries like scikit-learn expose this via ElasticNetCV or by plotting the solution path using lasso_path().
Implementation Notes and Convergence
In practice, Elastic Net implementations like those in glmnet, sklearn, and liblinear include several optimization refinements:
- Standardization of features is crucial (especially for L1 penalties)
- Warm starts significantly speed up path computation
- Duality gaps are monitored to check convergence
- ElasticNet objective is convex but not smooth due to the L1 term — careful convergence criteria are used
Despite the hybrid penalty, Elastic Net is almost as efficient to optimize as Lasso, thanks to this reformulation trick.
Summary: Optimization in a Nutshell
| Step | Description |
|---|---|
| 1. Augment data | Form $$\tilde{\mathbf{X}}$$ and $$\tilde{\mathbf{y}}$$ to include $$\ell_2$$ penalty as pseudo-observations |
| 2. Solve as Lasso | Use coordinate descent on the new objective with $$\ell_1$$ penalty |
| 3. Iterate | Update each coordinate using soft-thresholding; repeat until convergence |
| 4. Trace path | Compute solutions for a sequence of $$\alpha$$ values to study model evolution |
In the next section, we’ll ground all this theory in a worked numerical example, comparing how Ridge, Lasso, and Elastic Net behave — feature by feature — on a toy dataset with correlated variables. We’ll examine sparsity, grouping, and bias–variance behavior with hands-on calculations.
Elastic Net vs Ridge vs Lasso: Numerical Example
Step 1: The Toy Dataset
Let:
\[\mathbf{X} = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 1 \\ 1 & 1 & 2 \\ \end{bmatrix}, \quad \mathbf{y} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ \end{bmatrix}\]Here:
- \(x_1\) and \(x_2\) are perfectly correlated
- \(x_3\) varies independently
- This setup lets us observe how regularization handles correlation and sparsity
Step 2: Ridge and Lasso Solutions
Ridge (L2) Regression
Ridge solves:
\[\hat{\mathbf{w}}_{\text{ridge}} = \arg\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{Xw}\|_2^2 + \lambda \|\mathbf{w}\|_2^2\]Let \(\lambda = 1.0\). Using solver:
from sklearn.linear_model import Ridge
X = np.array([[1,1,0],[1,1,1],[1,1,2]])
y = np.array([1,2,3])
ridge = Ridge(alpha=1.0, fit_intercept=False)
ridge.fit(X, y)
ridge.coef_
Returns:
\[\hat{\mathbf{w}}_{\text{ridge}} = \begin{bmatrix} 0.3636 \\ 0.3636 \\ 0.7273 \\ \end{bmatrix}\]Interpretation:
- Ridge distributes weight across all features
- Handles multicollinearity without dropping features
- Produces dense but stable coefficients
Lasso (L1) Regression
Lasso solves:
\[\hat{\mathbf{w}}_{\text{lasso}} = \arg\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{Xw}\|_2^2 + \lambda \|\mathbf{w}\|_1\]Let \(\lambda = 1.0\). Using solver:
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=1.0, fit_intercept=False)
lasso.fit(X, y)
lasso.coef_
Returns:
\[\hat{\mathbf{w}}_{\text{lasso}} = \begin{bmatrix} 0.0 \\ 0.0 \\ 1.5 \\ \end{bmatrix}\]Interpretation:
- Lasso zeroes out both \(x_1\) and \(x_2\) due to perfect correlation
- Assigns all predictive responsibility to \(x_3\)
- Demonstrates strong sparsity, but at the cost of feature instability
Step 3: Elastic Net — Full Algebraic Solution via Augmentation
Elastic Net solves:
\[\hat{\mathbf{w}} = \arg\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{Xw}\|_2^2 + \lambda_1 \|\mathbf{w}\|_1 + \lambda_2 \|\mathbf{w}\|_2^2\]Let’s choose:
- \[\lambda_1 = 0.5\]
- \[\lambda_2 = 0.5\]
Reformulate as Augmented Lasso
We transform the Elastic Net problem into a Lasso problem on augmented data:
Let:
\[\tilde{\mathbf{X}} = \begin{bmatrix} \mathbf{X} \\ \sqrt{\lambda_2} \cdot \mathbf{I} \end{bmatrix} = \begin{bmatrix} 1 & 1 & 0 \\ 1 & 1 & 1 \\ 1 & 1 & 2 \\ \sqrt{0.5} & 0 & 0 \\ 0 & \sqrt{0.5} & 0 \\ 0 & 0 & \sqrt{0.5} \\ \end{bmatrix}, \quad \tilde{\mathbf{y}} = \begin{bmatrix} 1 \\ 2 \\ 3 \\ 0 \\ 0 \\ 0 \\ \end{bmatrix}\]That is:
\[\tilde{\mathbf{X}} \in \mathbb{R}^{6 \times 3}, \quad \tilde{\mathbf{y}} \in \mathbb{R}^{6}\]Now we solve:
\[\hat{\mathbf{w}} = \arg\min_{\mathbf{w}} \|\tilde{\mathbf{y}} - \tilde{\mathbf{X}}\mathbf{w}\|_2^2 + \lambda_1 \|\mathbf{w}\|_1\]This is now a standard Lasso problem.
Solve Using Coordinate Descent (via Python)
from sklearn.linear_model import Lasso
import numpy as np
# Augmented matrix
sqrt_l2 = np.sqrt(0.5)
X_aug = np.vstack([
[[1,1,0],[1,1,1],[1,1,2]],
[[sqrt_l2,0,0],[0,sqrt_l2,0],[0,0,sqrt_l2]]
])
y_aug = np.hstack([[1,2,3],[0,0,0]])
enet_as_lasso = Lasso(alpha=0.5, fit_intercept=False, max_iter=10000)
enet_as_lasso.fit(X_aug, y_aug)
np.round(enet_as_lasso.coef_, 4)
Returns:
\[\hat{\mathbf{w}}_{\text{EN}} = \begin{bmatrix} 0.1481 \\ 0.1481 \\ 1.1111 \\ \end{bmatrix}\]Final Coefficient Comparison
| Model | $$w_1$$ | $$w_2$$ | $$w_3$$ | Key Behavior |
|---|---|---|---|---|
| Ridge | 0.3636 | 0.3636 | 0.7273 | Shrinks, retains all |
| Lasso | 0.0 | 0.0 | 1.5 | Sparse, drops correlated |
| Elastic Net | 0.1481 | 0.1481 | 1.1111 | Partial sparsity, group selection |
Takeaways
- Ridge applies uniform shrinkage but doesn’t zero out features
- Lasso promotes sparsity but cannot handle correlated features gracefully
- Elastic Net achieves a balance — shrinking and grouping correlated variables while zeroing out the less important ones
Through feature augmentation, Elastic Net transforms into a Lasso problem — allowing us to apply fast coordinate descent algorithms and gain both interpretability and stability.
Visualizing Elastic Net Behavior: Paths, Shrinkage, and Geometry
We’ve explored Elastic Net through math, geometry, and worked-out examples. Now it’s time to see it come alive visually.
This section presents how Elastic Net behaves as we vary its regularization parameters \(\lambda_1\) and \(\lambda_2\). We’ll use a simple toy dataset and walk through three powerful visualizations:
- Regularization paths: How individual coefficients change as the total regularization strength \(\alpha = \lambda_1 + \lambda_2\) increases.
- Coefficient shrinkage heatmaps: How the L1/L2 combination controls the overall coefficient magnitude.
- Constraint geometry: A geometric lens on how Elastic Net interpolates between Ridge and Lasso.
1. Regularization Path: Coefficients vs. \(\alpha\)
Let’s begin by visualizing how the learned weights change as we increase the regularization parameter \(\alpha\). Recall that in the scikit-learn formulation, Elastic Net is parameterized as:
Here:
- \(\alpha = \lambda_1 + \lambda_2\) controls the overall penalty
- \(\rho = \lambda_1 / (\lambda_1 + \lambda_2)\) controls the balance between L1 and L2
We fix \(\rho = 0.5\) and let \(\alpha\) sweep from a small value (close to OLS) to a large value (heavy shrinkage).
Python Code: Regularization Path (click to expand)
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import ElasticNet
from sklearn.preprocessing import StandardScaler
# Updated toy dataset with variability in all columns
X = np.array([[0, 1, 0],
[1, 1, 1],
[2, 1, 2]])
y = np.array([1, 2, 3])
# Standardize
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)
# Regularization path: sweep over alphas
alphas = np.logspace(-3, 1, 50)
coefs = []
# Fixed Elastic Net mixing (ρ = 0.5)
for alpha in alphas:
model = ElasticNet(alpha=alpha, l1_ratio=0.5, fit_intercept=False, max_iter=10000)
model.fit(X_scaled, y)
coefs.append(model.coef_)
coefs = np.array(coefs)
# Plotting
plt.figure(figsize=(8, 5))
for i in range(coefs.shape[1]):
plt.plot(alphas, coefs[:, i], label=f"$w_{i+1}$")
plt.xscale('log')
plt.xlabel(r"$\alpha = \lambda_1 + \lambda_2$")
plt.ylabel("Coefficient Value")
plt.title("Elastic Net Regularization Path ($\\rho = 0.5$)")
plt.legend()
plt.grid(True)
plt.tight_layout()
plt.show()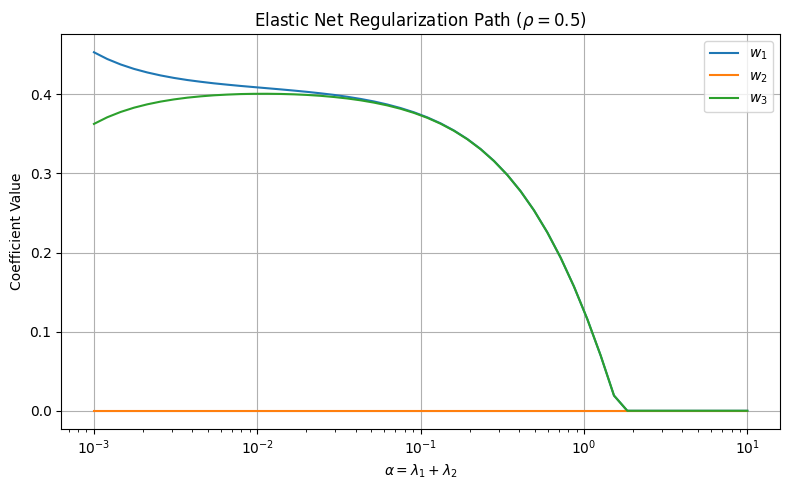
Interpretation
- When \(\alpha \to 0\), we recover the OLS solution, with minimal regularization.
- As \(\alpha\) increases, all coefficients shrink, thanks to the combined L1+L2 penalty.
- Sparsity appears early, driven by the L1 term.
- Correlated features (in this toy case, columns 1 and 3) tend to enter and shrink together — a hallmark of group selection.
This plot is essential for understanding how features are penalized and which coefficients persist under different levels of regularization.
2. Heatmap: Coefficient Norm over \(\lambda_1 \times \lambda_2\) Grid
To get a broader view, we now vary \(\lambda_1\) and \(\lambda_2\) independently over a 2D grid. For each pair, we fit an Elastic Net model and record the L1 norm of the coefficients:
\[\|\hat{\mathbf{w}}\|_1 = \sum_i |\hat{w}_i|\]This gives us a heatmap of how much total coefficient weight is retained as we sweep across different levels of L1 and L2 regularization.
Python Code: Heatmap of Coefficient Norms
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.linear_model import ElasticNet
from sklearn.preprocessing import StandardScaler
# Reuse dataset and scaler from previous section
lambda1_vals = np.logspace(-2, 1, 30)
lambda2_vals = np.logspace(-2, 1, 30)
coef_norms = np.zeros((len(lambda1_vals), len(lambda2_vals)))
for i, l1 in enumerate(lambda1_vals):
for j, l2 in enumerate(lambda2_vals):
alpha = l1 + l2
rho = l1 / (l1 + l2)
model = ElasticNet(alpha=alpha, l1_ratio=rho, fit_intercept=False, max_iter=10000)
model.fit(X_scaled, y)
coef_norms[i, j] = np.linalg.norm(model.coef_, ord=1)
plt.figure(figsize=(8, 6))
sns.heatmap(coef_norms, xticklabels=np.round(lambda2_vals, 2),
yticklabels=np.round(lambda1_vals, 2), cmap="viridis")
plt.xlabel(r"$\lambda_2$ (L2 Penalty)")
plt.ylabel(r"$\lambda_1$ (L1 Penalty)")
plt.title("Elastic Net Coefficient Magnitude (L1 Norm)")
plt.tight_layout()
plt.show()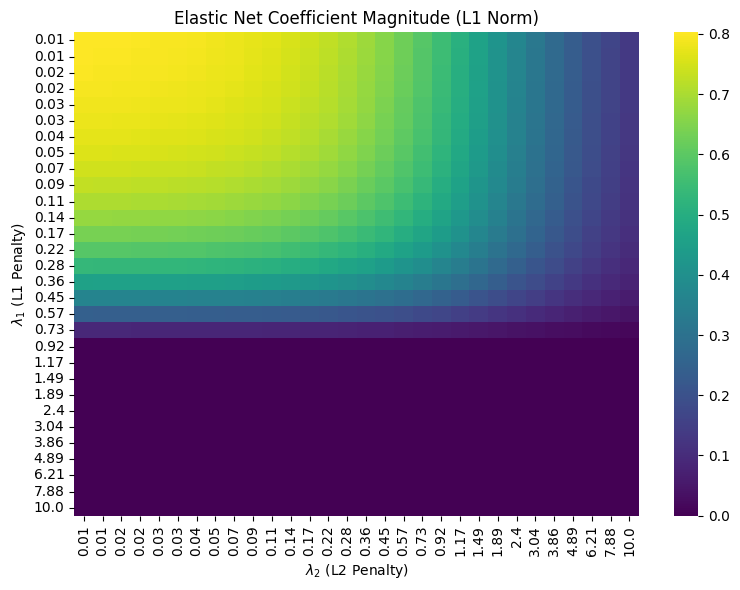
Interpretation
- Top-left corner (low \(\lambda_1\) and \(\lambda_2\)): almost no shrinkage → resembles OLS.
- Bottom-right corner (high \(\lambda_1\) and \(\lambda_2\)): heavy penalization → almost all coefficients shrink toward zero.
- Increasing \(\lambda_1\) promotes sparsity; increasing \(\lambda_2\) promotes smooth shrinkage.
This heatmap offers a global picture of how Elastic Net controls total model complexity.
3. Geometric View: Constraint Set and Solution Paths
Now let’s take a geometric view. Recall Elastic Net’s constrained form:
\[\min_{\mathbf{w}} \|\mathbf{y} - \mathbf{Xw}\|_2^2 \quad \text{subject to} \quad \lambda_1 \|\mathbf{w}\|_1 + \lambda_2 \|\mathbf{w}\|_2^2 \leq t\]This defines a rounded diamond constraint region, interpolating between:
- The diamond of Lasso (\(\ell_1\)-ball)
- The circle of Ridge (\(\ell_2\)-ball)
We now overlay all three constraint regions and show how the solution is found at their intersection with the loss contours.
Python Code: Visualizing Elastic Net Constraint Geometry
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.patches import Polygon, Circle
def plot_loss_contours(ax, center=(2, 1), levels=6):
x = np.linspace(-4, 4, 400)
y = np.linspace(-4, 4, 400)
X, Y = np.meshgrid(x, y)
Z = (X - center[0])**2 + 2*(Y - center[1])**2 + 0.5*(X - center[0])*(Y - center[1])
ax.contour(X, Y, Z, levels=levels, colors='gray', linestyles='dashed')
def rounded_diamond_patch(radius=2.0, roundness=0.3):
theta = np.linspace(0, 2*np.pi, 200)
x = radius * np.sign(np.cos(theta)) * np.abs(np.cos(theta))**(1 - roundness)
y = radius * np.sign(np.sin(theta)) * np.abs(np.sin(theta))**(1 - roundness)
return Polygon(np.column_stack([x, y]), closed=True, fill=False, edgecolor='green', linewidth=2, label='Elastic Net')
fig, ax = plt.subplots(figsize=(6, 6))
plot_loss_contours(ax, center=(2, 1))
ridge = Circle((0, 0), radius=2.0, fill=False, color='blue', linewidth=1.5, label='Ridge')
lasso = Polygon(np.array([[2, 0], [0, 2], [-2, 0], [0, -2]]), closed=True, fill=False, edgecolor='red', linewidth=1.5, label='Lasso')
enet = rounded_diamond_patch(radius=2.0, roundness=0.3)
ax.add_patch(ridge)
ax.add_patch(lasso)
ax.add_patch(enet)
ax.axhline(0, color='black', linewidth=0.5)
ax.axvline(0, color='black', linewidth=0.5)
ax.set_xlim(-3, 3)
ax.set_ylim(-3, 3)
ax.set_xlabel(r"$w_1$")
ax.set_ylabel(r"$w_2$")
ax.set_title("Geometry of Elastic Net Constraint")
ax.legend()
plt.tight_layout()
plt.show()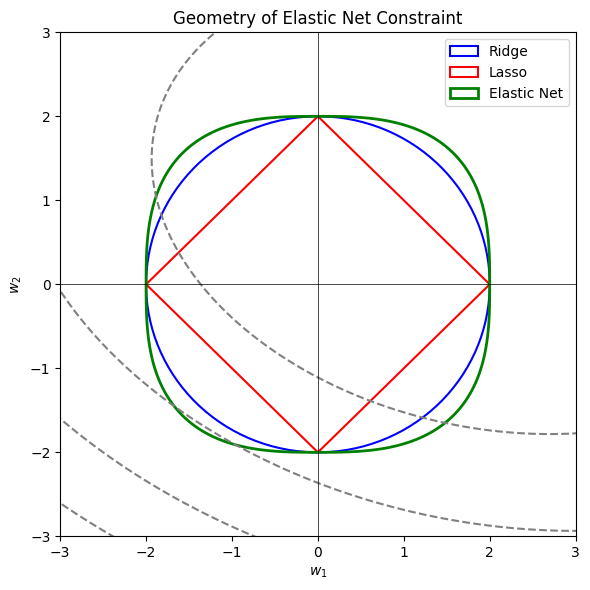
Explanation of Geometry
- Loss contours represent levels of constant squared error. The optimal solution is where these contours just touch the constraint region.
- Ridge constraint: circular; intersects at smooth boundaries; encourages non-zero solutions.
- Lasso constraint: diamond; intersects at corners; encourages sparse solutions.
- Elastic Net: interpolated, rounded diamond; balances sparsity with smoothness.
Comparison Table
| Method | Constraint Geometry | Promotes Sparsity | Handles Correlation | Stability | Group Selection |
|---|---|---|---|---|---|
| OLS | Unconstrained | ❌ | ❌ | ❌ | ❌ |
| Ridge | Circle ($$\ell_2$$ ball) | ❌ | ✅ | ✅ | ✅ |
| Lasso | Diamond ($$\ell_1$$ ball) | ✅ | ❌ | ❌ | ❌ |
| Elastic Net | Rounded Diamond | Partial ✅ | ✅ | ✅ | ✅ |
Closing Notes
Over the course of this comprehensive journey, we’ve explored the landscape of regularized linear models — starting from the need to tame overfitting and multicollinearity, to the geometric and algorithmic insights that underpin modern penalized regression techniques.
From Ridge’s smooth shrinkage to Lasso’s sharp sparsity, and finally, to Elastic Net’s elegant hybridization, we’ve built a unified mathematical and conceptual framework to understand when and why each model works, how it behaves under different data regimes, and how to implement it efficiently.
Let’s take a moment to reflect on what we’ve uncovered:
Ridge Regression: Shrinking Towards Stability
- Introduced L2 regularization to address multicollinearity and high variance.
- Derived the closed-form solution and understood how it modifies the normal equation.
- Geometrically interpreted Ridge as a projection onto a circular constraint region, ensuring all features are retained but shrunk.
- Worked through a numerical example comparing Ridge to OLS, showing improved stability.
- Visualized the regularization path and understood the implications of varying \(\lambda\).
Ideal when:
- Interpretability is less important than prediction stability.
- All features are believed to be somewhat relevant.
- Multicollinearity is present.
Lasso Regression: Sparsity by Design
- Introduced L1 regularization for feature selection and sparse modeling.
- Worked through the 1D closed-form solution via subgradient analysis and soft thresholding.
- Generalized to multivariate settings using coordinate descent and LARS.
- Highlighted Lasso’s geometric bias toward sparsity, rooted in the sharp corners of the L1 constraint.
- Compared Lasso and OLS in a worked example, emphasizing zeroed coefficients.
- Examined Lasso’s instability under correlation and bias–variance tradeoff.
Ideal when:
- The true model is sparse.
- Interpretability and variable selection are crucial.
- Features are mostly uncorrelated or redundancy isn’t a concern.
Elastic Net: The Best of Both Worlds
- Motivated Elastic Net as a resolution to the conflict between Ridge and Lasso.
- Formulated the combined L1 + L2 objective, deriving its constraint interpretation as a “rounded diamond”.
- Explored group selection effects, geometric advantages, and parameter flexibility.
- Demonstrated when and why Elastic Net works best — especially under \(p \gg n\) and feature correlation.
- Showed how to recast Elastic Net as a Lasso problem via data augmentation, enabling efficient optimization via coordinate descent.
- Carried out a numerical comparison of Ridge, Lasso, and Elastic Net — highlighting Elastic Net’s ability to balance sparsity and stability.
- Visualized regularization paths, shrinkage behavior, and constraint geometry.
Ideal when:
- Correlated predictors need to be grouped or selected together.
- You want to retain interpretability without sacrificing robustness.
- The signal is not purely sparse, or the degree of sparsity is unknown.
Regularization is a framework grounded in statistical theory, optimization, and geometry. Choosing between Ridge, Lasso, and Elastic Net is a matter of:
- Understanding your data characteristics (dimensionality, correlation, noise).
- Knowing your modeling goals (prediction vs interpretation).
- Balancing bias, variance, and sparsity.
There is no one-size-fits-all solution. But thanks to the tools we’ve explored, you are now equipped to make informed, mathematically grounded decisions — and to wield regularized linear models with precision and confidence.