1. Introduction to Non-Parametric Models
2. K-Nearest Neighbors (KNN): The Starting Point
- 2.1 Core Principles of KNN
- 2.2 Why KNN Breaks Down — And What Comes Next
3. Decision Trees: The Building Blocks
Conclusion
- Motivation for Ensemble Methods

Most machine learning workflows today involve some form of ensemble learning—whether it’s a random forest powering a fraud detection pipeline, a gradient boosting model ranking search results, or a stacked model optimizing recommendation systems. But ensemble methods don’t appear out of nowhere. They are built on top of core, foundational algorithms—most notably decision trees.

Before diving into ensembles themselves, it’s essential to understand the models they assemble. This first post begins by grounding the series in the non-parametric learning paradigm: a class of models that avoid strong assumptions about the underlying data distribution, and instead learn patterns directly from data with flexible, adaptive complexity. These models are often where practitioners first encounter data-dependent model structures, local reasoning, and sensitivity to distance or feature partitioning.

We’ll begin with K-Nearest Neighbors (KNN), a classic example of instance-based learning that performs surprisingly well in certain regimes despite its simplicity. Its strengths and weaknesses naturally lead us to decision trees, which bring both structure and interpretability to non-parametric learning. Trees introduce important ideas—recursive partitioning, impurity measures, overfitting via deep branching, and the need for pruning—that will later resurface when we discuss bagging, boosting, and stacking.

This post is not a surface-level overview. We’ll go through how non-parametric models differ from parametric ones in theory and practice, walk through KNN’s design choices and scaling issues, and analyze how decision trees split data, how they fail, and how they form the building blocks of more sophisticated ensembles.

The goal is simple: to establish a strong conceptual foundation so that when we start assembling models in future posts—combining trees into forests or optimizing sequences of learners—we do so with a clear understanding of the components involved and the trade-offs they carry.

Let’s begin with the non-parametric mindset.

1. Introduction to Non-Parametric Models

1.1 Why Non-Parametric Models?

In classical machine learning, we often differentiate models based on whether they make strict assumptions about the underlying data-generating process. Parametric models, such as linear regression or logistic regression, assume a fixed functional form defined by a finite set of parameters. For instance, linear regression assumes the target variable is a linear function of input features. While these assumptions offer simplicity and interpretability, they can be overly restrictive in real-world settings where data relationships are complex, noisy, or unknown.

In contrast, non-parametric models do not assume a fixed structure. Instead, they adapt their complexity to the dataset at hand. As more data becomes available, they can learn increasingly intricate patterns without being constrained by a predefined model form. This is particularly useful in domains where the relationship between features and target variables is highly non-linear, or where multiple modes, interactions, or thresholds exist in the data.

Key Strengths of Non-Parametric Models:

Flexibility: They can model arbitrary functions given enough data.
Minimal assumptions: No need to specify the form of the function beforehand.
Data-adaptive: Their effective complexity grows with the size of the dataset.

However, this flexibility comes at a cost. Without proper controls (e.g., regularization, pruning, cross-validation), non-parametric models are prone to overfitting—capturing noise in the training data instead of generalizable patterns. This necessitates careful validation and tuning strategies to ensure robust performance on unseen data.

When Flexibility Matters:

Consider a scenario in fraud detection where fraudulent behavior patterns evolve rapidly and vary across different regions and user segments. A parametric model like logistic regression may struggle to capture these shifts due to its fixed form. A non-parametric model, such as a decision tree or ensemble of trees, can dynamically partition the feature space to isolate such irregularities.

1.2 Parametric vs. Non-Parametric: A Comparative View

Let’s distill the key differences between these two model families:

Model Type	Assumptions	Flexibility	Risk	Key Trade-Off
Parametric	Strong (e.g., linear)	Low	Underfitting	High bias, low variance
Non-Parametric	Minimal	High	Overfitting	Low bias, high variance

The bias–variance trade-off is central here. Parametric models have high bias (they may oversimplify complex relationships) but low variance (small changes in data don’t affect them much). Non-parametric models, on the other hand, have the potential for low bias but may exhibit high variance unless controlled carefully.

1.3 Examples of Non-Parametric Models

Here are some prominent non-parametric models widely used in machine learning:

K-Nearest Neighbors (KNN): A lazy learning algorithm that makes predictions based on the majority class or mean outcome of the k closest training samples. It is completely instance-based and adapts fully to the shape of the data.
Decision Trees: Tree-structured models that recursively split the input space based on feature thresholds. They do not assume linearity and are naturally suited for mixed data types.
Support Vector Machines (SVMs): While the linear form of SVM is parametric, SVMs with kernels (e.g., RBF, polynomial) are considered non-parametric as the model complexity is driven by support vectors rather than fixed parameters.
Gaussian Processes (GPs): Probabilistic models that define a distribution over functions. GPs provide a flexible Bayesian framework with uncertainty estimates and adapt their complexity as more data is observed.

Each of these models offers different strengths depending on the dataset size, feature dimensionality, and modeling objective. Later sections of this blog series will dive into these models individually, starting with KNN and Decision Trees.

1.4 Use Cases and Applications

Non-parametric models are especially useful in domains where the structure of the data is unknown or inherently complex. Their ability to adapt to the data makes them powerful tools in real-world applications:

Domain	Problem Type	Why Non-Parametric Models Help
Healthcare	Predicting patient risk	Captures non-linear interactions among lab results, demographics, and symptoms
Marketing	Customer segmentation	Adapts to varying behavior patterns across regions, channels, or age groups
Finance	Fraud detection	Flexible enough to capture rare but complex patterns in transactional data
Computer Vision	Image classification	Avoids fixed assumptions, relies on local neighborhood or learned structure

These applications reflect the versatility of non-parametric methods in both structured and unstructured data contexts. Whether the task involves tabular risk modeling, spatial classification, or dynamic segmentation, non-parametric approaches often offer superior adaptability.

1.5 When to Prefer Non-Parametric Approaches

Knowing when to reach for a non-parametric model is crucial. Here are some key scenarios where they typically outperform parametric alternatives:

Presence of non-linear relationships: When relationships among features and targets are not linearly separable or cannot be modeled through simple transformations.
Complex or unknown distributions: When the data is noisy, multimodal, or doesn’t conform to standard statistical distributions.
Mixed or categorical data: Decision trees and their ensembles handle categorical and numerical features with minimal preprocessing.
Limited prior domain knowledge: In exploratory modeling phases, non-parametric models can serve as powerful baselines due to their ability to discover hidden structures.
Large datasets: Since non-parametric models can grow in complexity with more data, they often perform better in data-rich environments where parametric models might underfit.

However, they may not be ideal when:

Data is scarce (risk of overfitting),
Real-time inference is critical (some non-parametric models are computationally heavy),
Interpretability is paramount (though some like trees are interpretable, others like SVMs with RBF kernel or GPs are less so).

In practice, it’s often beneficial to compare both model types. Start simple with parametric baselines, then move to non-parametric models if performance, flexibility, or structure discovery becomes a priority.

2. K-Nearest Neighbors (KNN): The Starting Point

2.1 Core Principles of KNN

The K-Nearest Neighbors (KNN) algorithm is often the first model introduced in machine learning courses—and for good reason. It embodies the simplest non-parametric learning strategy, requiring virtually no assumptions about the underlying data distribution. Despite its simplicity, KNN is surprisingly effective in many real-world tasks and serves as an important conceptual anchor for understanding more complex models, particularly those grounded in the idea of local decision-making. Let’s unpack the core principles that define how KNN learns and predicts.

2.1.1 Instance-Based Learning

KNN belongs to the broader family of instance-based or memory-based learning algorithms. These models defer generalization until prediction time, rather than compressing the training data into a parameterized model. That means KNN does not attempt to form a summary or abstraction of the data during training. Instead, it retains the entire training dataset as its “model.”

When a new test input $\mathbf{x}$ arrives, KNN performs a similarity search: it identifies the $k$ training points closest to $\mathbf{x}$ in feature space and uses them to determine the output. This behavior is fundamentally different from parametric models like logistic regression, which learn a fixed set of coefficients and discard the training data post-training.

The instance-based nature of KNN makes it:

Flexible, since it can model complex and nonlinear decision boundaries.
Simple to update, because new training examples can be immediately incorporated by appending them to the stored dataset.
Sensitive to data quality, because irrelevant or noisy instances can influence predictions directly.

KNN’s reliance on storing examples means it can be viewed as a form of rote memorization. This is not necessarily a flaw—it’s a design choice that trades storage and computation for flexibility and ease of use.

2.1.2 Distance-Based Decision-Making

At its core, KNN operates under a simple inductive bias:

Nearby points in feature space are likely to have similar outputs.

To implement this principle, KNN uses a distance metric to determine the closeness between points. The most commonly used metrics are:

Euclidean Distance (L2 norm):
\[d(\mathbf{x}, \mathbf{x}') = \sqrt{\sum_{j=1}^{d} (x_j - x_j')^2}\]
Manhattan Distance (L1 norm):
\[d(\mathbf{x}, \mathbf{x}') = \sum_{j=1}^{d} |x_j - x_j'|\]
Minkowski Distance (Generalization):
\[d(\mathbf{x}, \mathbf{x}') = \left( \sum_{j=1}^{d} |x_j - x_j'|^p \right)^{1/p}\]
Cosine Distance: Often used when direction matters more than magnitude (e.g., in text classification).
Mahalanobis Distance: Takes into account feature correlations and scale.

KNN predicts the label for a test instance by aggregating the labels of its $k$ nearest neighbors. In classification, this typically means taking a majority vote; in regression, it means averaging the numerical labels.

Formally, for a test point $\mathbf{x}_{\text{test}}$,

KNN identifies a set $S \subset \mathcal{D}_{\text{train}}$ of $k$ training points such that:

\[S = \text{argmin}_S \sum_{\mathbf{x}_i \in S} d(\mathbf{x}_{\text{test}}, \mathbf{x}_i)\]

Then the predicted output is:

For classification: the mode of the labels in $S$
For regression: the mean of the labels in $S$

This mechanism emphasizes the local structure of the data: the prediction is derived from the neighborhood immediately surrounding the test point.

2.1.3 Lazy Learning: No Explicit Training Phase

Unlike many ML models, KNN does not involve a separate training process in the traditional sense. There is no fitting of weights, no gradient descent, no objective function to minimize. Instead, the algorithm simply memorizes the training data.

This learning style is known as lazy learning. All the work is pushed to the prediction phase, where the algorithm must search through the entire training set to identify the nearest neighbors to a given query. As a result, prediction latency can be high, particularly with large datasets.

Here’s a contrast between lazy and eager learning:

Characteristic	Lazy Learning (e.g., KNN)	Eager Learning (e.g., Logistic Regression)
Training phase	Just stores the training data	Fits a model using optimization
Prediction phase	High cost: computes distances from scratch	Fast: evaluates a trained function
Flexibility	High: no assumptions about model form	Lower: constrained by model class
Data addition	Easy: append to stored set	Harder: may require retraining
Memory usage	High	Low

This makes KNN ideal in low-latency training, high-latency inference settings, such as online learning or interactive systems where new data constantly arrives and training must be nearly instantaneous.

However, this also means KNN scales poorly as the number of training samples grows—both in terms of memory and prediction time. Specialized data structures such as KD-Trees, Ball Trees, or Approximate Nearest Neighbor techniques can mitigate some of these issues, especially in low to moderate dimensions.

In summary, KNN’s learning strategy is defined by three core principles:

Instance-based learning: The algorithm learns by storing and referencing examples rather than abstracting them into a model.
Distance-based prediction: Similarity in feature space determines prediction; this makes feature scaling and distance metric choice critical.
Lazy learning: No training cost, but potentially expensive predictions due to real-time neighbor search.

These features make KNN simple to implement and valuable as a baseline, particularly in settings where the decision boundaries are complex or poorly understood. However, they also foreshadow some of KNN’s limitations, especially in terms of scalability and sensitivity to irrelevant or redundant features—topics we will explore in upcoming sections.

2.2 Why KNN Breaks Down — And What Comes Next

While K-Nearest Neighbors (KNN) offers a refreshingly simple approach to classification and regression—no training phase, minimal assumptions, and intuitive behavior—its practicality fades as datasets grow in size, complexity, or dimensionality. In this section, we critically examine KNN’s key limitations and why they compel us to move toward more structured, scalable models like decision trees, especially in modern data science workflows.

2.2.1 The Curse of Dimensionality

One of the most profound limitations of K-Nearest Neighbors lies in its vulnerability to the curse of dimensionality. At its core, KNN assumes that similar instances lie close to each other in the feature space. But as dimensionality increases, the geometry of high-dimensional spaces undermines this assumption in both theoretical and practical ways.

Sparsity in High Dimensions

In low dimensions, data points can be densely packed. For example, a simple 1D interval $[0, 1]$ can be covered adequately with 100 points. However, to achieve the same resolution in 10 dimensions, you would require:

\[100^{10} = 10^{20}\]

points—an astronomical number.

This exponential blow-up of volume causes high-dimensional spaces to become extremely sparse. As a result, every point becomes far from every other point, and the traditional notion of “closeness” used by KNN breaks down. In fact, the distances between the nearest and farthest neighbors converge:

\[\lim_{d \to \infty} \frac{\lVert \mathbf{x}_{\text{nearest}} - \mathbf{x} \rVert}{\lVert \mathbf{x}_{\text{farthest}} - \mathbf{x} \rVert} \to 1\]

Volume-Based Intuition: Neighborhood Size Grows

Suppose you have a dataset of $n$ points uniformly distributed in the unit hypercube $[0,1]^d$. For a test point, you want to find the smallest cube around it (centered at the test point) that contains its $k$-nearest neighbors.

Let:

$\ell^d$ be the volume of that cube (since all sides have length $\ell$),
and $k/n$ be the fraction of the total dataset you want to enclose.

So, to capture $k$ out of $n$ points, you want the volume of your cube to be approximately:

\[\ell^d = \frac{k}{n}\]

Solving for $\ell$:

\[\ell = \left( \frac{k}{n} \right)^{1/d}\]

Why This Gets Bad as $d$ Increases

Let’s say you fix $k/n = 0.01$, meaning you want to capture the closest 1% of your dataset. That seems reasonable — KNN shouldn’t use the entire dataset for one prediction.

Now observe what happens to $\ell$ as $d$ increases:

Let’s fix:

$k/n = 0.01$

Then:

$d = 2 \Rightarrow \ell = (0.01)^{1/2} \approx 0.1$
$d = 10 \Rightarrow \ell = (0.01)^{1/10} \approx 0.63$
$d = 100 \Rightarrow \ell = (0.01)^{1/100} \approx 0.955$
$d = 1000 \Rightarrow \ell = (0.01)^{1/1000} \approx 0.9954$

As you can see, the required neighborhood edge length grows rapidly — approaching 1. That means the neighborhood must expand to cover nearly the entire feature space just to capture 1% of the data!

The visualization below illustrates how the edge length ($\ell$) of a neighborhood cube must expand as the dimensionality ($d$) of the feature space increases—even when we fix the proportion of neighbors to just 1% of the dataset.

Each inner colored cube corresponds to a different value of $d$:

Blue for $d = 2$: $\ell \approx 0.1$
Green for $d = 10$: $\ell \approx 0.63$
Red for $d = 100$: $\ell \approx 0.955$

The gray outer cube is the full unit cube $[0, 1]^3$ used for reference. As you increase $d$, the inner cube grows rapidly in size and nearly fills the entire unit cube. This demonstrates how, in high-dimensional spaces, you must include most of the dataset just to define a local neighborhood.

Such geometric expansion undermines the core principle of KNN—that nearby points are meaningfully similar—because in high dimensions, there’s no meaningful “nearby” anymore.

This tells us that in high dimensions:

To capture a small fraction of the dataset, your “local” neighborhood must cover almost the whole space.
But if you include nearly everything, the model is no longer local.
And that defeats the core logic of KNN — that local proximity implies label similarity.

Thus, even when you try to shrink the number of neighbors $k$, you’re forced to increase the geometric size $\ell$ of your neighborhood. And that destroys the granularity and discriminative power of distance-based methods.

To estimate the edge length $\ell$ of the neighborhood cube that encloses $k$ out of $n$ points in $d$-dimensions:

\[\ell = \left( \frac{k}{n} \right)^{1/d}\]

As $d \to \infty$, $\ell \to 1$, even for small $k/n$. This shows why high-dimensional KNN neighborhoods become huge, forcing the algorithm to average over large, irrelevant regions of space.

Distance Concentration and Theoretical Collapse

Not only do neighborhoods expand, but distances between points concentrate. As dimensionality increases, most pairwise distances fall within a narrow range. When every point is approximately the same distance from every other, selecting the “nearest” neighbor becomes meaningless.

Moreover, shrinking the neighborhood to retain locality becomes infeasible. The number of training points required to keep the neighborhood size fixed shrinks as:

\[n \approx k \cdot \left(\frac{1}{\ell}\right)^d\]

Trying to shrink $\ell$ to just 0.1 in 100 dimensions would require:

\[n = k \cdot 10^{100}\]

points—completely intractable.

Classifier Boundaries and Adversarial Fragility

While pairwise distances grow and concentrate, the distance to a decision hyperplane remains unchanged, as orthogonal dimensions don’t affect the perpendicular projection. This leads to a strange situation:

Points are far from each other.
Yet they lie close to decision boundaries.

This geometric quirk makes high-dimensional models like SVMs susceptible to adversarial attacks and instability near hyperplanes.

Computational Burden of KNN in High Dimensions

KNN also becomes expensive to compute in high-dimensional regimes:

Prediction time is $O(n)$, since all distances must be computed.
Storage cost grows linearly with the size of the dataset.
Approximation techniques (e.g., KD-Trees, Ball Trees) fail beyond 20–30 dimensions.

Without aggressive dimensionality reduction, KNN becomes both computationally and statistically infeasible.

Practical Mitigations and When KNN Still Works

There are strategies to reduce the impact of high dimensionality:

Feature Scaling: Ensure uniform scaling across features to avoid bias in distance computation.
Dimensionality Reduction: PCA, UMAP, or t-SNE can uncover low-dimensional structure.
Metric Selection: Use Mahalanobis or Hamming distance where appropriate.

Moreover, many real-world datasets live on low-dimensional manifolds even if embedded in a high-dimensional ambient space. When this is true, and the intrinsic dimensionality is low, KNN can still work well.

Summary

The curse of dimensionality undermines the foundation of KNN by:

Making all points nearly equidistant.
Expanding neighborhood volumes.
Breaking assumptions of locality and similarity.
Exponentially increasing data and compute requirements.

KNN remains useful for low to moderate dimensional problems or when careful preprocessing reduces dimensionality. But beyond that, its effectiveness collapses—motivating our next transition to tree-based models, which partition space hierarchically instead of relying on raw distance.

2.2.2 Strengths and Weaknesses of KNN

To summarize KNN’s behavior across practical axes:

Aspect	KNN Strengths	KNN Weaknesses
Model Assumptions	None—purely data-driven	No inductive bias → prone to overfitting
Implementation	Trivial to code and understand	Prediction is slow for large datasets
Flexibility	Can model arbitrarily complex boundaries	Very sensitive to noise and irrelevant features
Memory Usage	None during training	High—must store full dataset
Interpretability	Transparent local reasoning (via neighbor inspection)	Hard to explain why a prediction was made globally
Scalability	Reasonable for small, low-dimensional datasets	Poor for big, high-dimensional data

2.2.3 Why KNN Isn’t Enough — Enter Tree-Based Models

Given these limitations, it’s natural to ask: Can we do better without losing the flexibility of non-parametric learning?

KNN offers a view of local structure but lacks:

Global model abstraction
Fast inference
Robustness to high-dimensionality
Model interpretability

This motivates a move toward decision trees, which preserve KNN’s non-parametric spirit but impose explicit hierarchical structure on the input space. Trees split the feature space into axis-aligned regions and associate labels or outputs with each region. Unlike KNN, which evaluates the entire training set for every query, trees pre-partition the space, enabling:

Faster predictions
More interpretable decision paths
Built-in feature selection via splits
Regularization via pruning

Moreover, decision trees serve as the foundational units in ensemble methods like Random Forests and Gradient Boosting, which overcome the instability of individual trees and offer state-of-the-art performance in many practical tasks.

Natural Pivot: What’s Next?

Having seen how KNN models decision boundaries using instance similarity, we now explore how decision trees achieve similar goals—but with model-based structure that improves speed, interpretability, and scalability. The next section builds the core understanding of how trees recursively partition the input space and make decisions through learned rules.

Let’s begin with the anatomy of a decision tree: nodes, branches, splits—and the criteria that guide them.

3. Decision Trees: The Building Blocks

3.1 Structure and Terminology

Decision trees are arguably the most intuitive models in the machine learning toolkit. They mirror human decision-making, breaking down complex decisions into a sequence of simple, interpretable rules. But to work effectively with them—whether for model building or interpretation—we must be clear on the anatomy of a tree.

Let’s walk through the foundational terms and concepts that define a decision tree.

The Anatomy of a Decision Tree

At a high level, a decision tree consists of:

Root Node
Internal Nodes
Leaf Nodes
Branches
Paths

Each part plays a specific role in how the tree ingests data and makes predictions.

Root Node

The topmost node of the tree.
Represents the entire dataset before any splitting.
Splits based on the best decision rule (e.g., maximizing information gain or minimizing Gini impurity).
This is where the recursive partitioning begins.

For example, in a dataset of customer churn, the root node might split first on “Tenure < 12 months”.

Internal Nodes (Decision Nodes)

Nodes that represent a decision point based on one of the input features.
Each internal node applies a test (e.g., “Age < 45”, “Income > 80000”).
Leads to two or more branches depending on the number of classes or outcomes in classification, or binary in most scikit-learn trees.

These nodes implement the core logic of the decision tree.

Leaf Nodes (Terminal Nodes)

Nodes that do not split further.
Represent the final prediction:
- In classification, this might be a class label (e.g., “Churn = Yes”).
- In regression, it’s a real value (e.g., predicted house price).

Leaf nodes also store information such as:

Number of samples falling into that node.
Class proportions (for classification).
Mean target value (for regression).

Branches

Directed edges connecting parent and child nodes.
Represent the outcome of a decision rule.
- E.g., if the node tests “Age < 45”, one branch might be labeled “True”, the other “False”.

Branches reflect the flow of logic from question to outcome.

Decision Paths

A path from the root node to a leaf node.
Represents a unique set of rules that a sample follows to reach its final prediction.
Can be interpreted as an if-else rule chain.

For instance:

IF Income > 80000 AND Age < 35 AND Tenure > 24 months THEN Churn = No

These rule chains make decision trees highly interpretable and useful for stakeholder explanations.

Visualizing Trees for Interpretability

Visual representations of decision trees are essential to understand the structure, interpret decision logic, identify overfitting, and communicate insights to stakeholders. A well-rendered tree shows not just what the model predicts, but why.

In this section, we generate and visualize a large, realistic decision tree trained on a synthetic employee attrition dataset. The tree learns from patterns such as salary, experience, department, distance from work, and overtime hours.

Tree Visualization from a Dataset

We trained a decision tree classifier on a dataset of 300 synthetic employee records. Each record includes features like:

Age, Experience, Education Level
Salary, Distance to Office
Department (HR, Tech, Sales, Admin, Legal)
Overtime Status
Work-Life Balance Score

Categorical variables were one-hot encoded, and the tree was grown with high depth (max_depth=10) and minimal pruning (min_samples_split=2, min_samples_leaf=1).

The result is a deep and expressive tree that mirrors how complex real-world patterns influence employee attrition.

Click to view visualization code

import pandas as pd
import numpy as np
from sklearn.tree import DecisionTreeClassifier, plot_tree
import matplotlib.pyplot as plt

# Generate larger dataset
np.random.seed(42)
n = 300  # Increased from 50 to 300

df = pd.DataFrame({
    'Age': np.random.randint(22, 60, size=n),
    'Experience': np.random.randint(0, 35, size=n),
    'Education_Level': np.random.choice([1, 2, 3], size=n, p=[0.3, 0.4, 0.3]),
    'Salary': np.random.randint(20000, 200000, size=n),
    'Department': np.random.choice(['HR', 'Tech', 'Sales', 'Admin', 'Legal'], size=n),
    'Overtime': np.random.choice(['Yes', 'No'], size=n, p=[0.4, 0.6]),
    'Distance': np.random.randint(1, 60, size=n),
    'WorkLifeBalance': np.random.randint(1, 5, size=n)
})

# One-hot encode categorical variables
df = pd.get_dummies(df, columns=['Department', 'Overtime'], drop_first=True)

# Simulate target variable with some hidden logic + noise
df['Attrition'] = (
    ((df['Experience'] < 3) & (df['Overtime_Yes'] == 1)) |
    ((df['Salary'] < 50000) & (df['Education_Level'] == 1)) |
    ((df['Distance'] > 40) & (df['WorkLifeBalance'] <= 2))
).astype(int)

# Feature set
X = df.drop(columns=['Attrition'])
y = df['Attrition']

# Fit a deeper tree
clf = DecisionTreeClassifier(
    max_depth=10, 
    min_samples_split=2, 
    min_samples_leaf=1, 
    random_state=42
)
clf.fit(X, y)

# Visualize the tree
plt.figure(figsize=(24, 14))
plot_tree(
    clf,
    feature_names=X.columns,
    class_names=['Stayed', 'Left'],
    filled=True,
    rounded=True,
    max_depth=5  # Show only top 5 levels for readability
)
plt.show()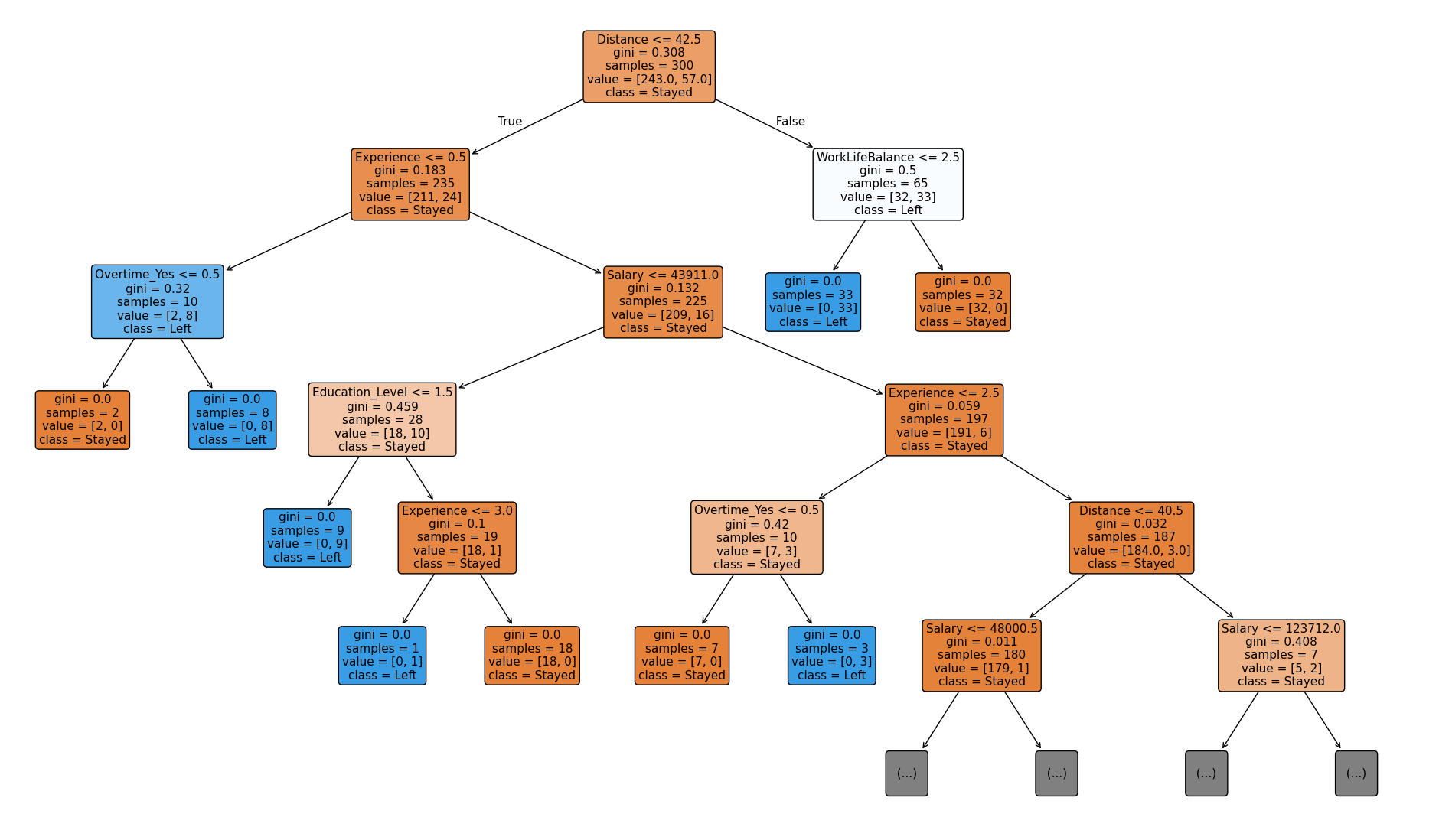

Interpreting the Tree Structure

Here’s what we observe from the top levels of the tree:

1. Primary Split: Experience < 3

The root node almost always splits on experience, separating junior employees from the rest. This reflects the intuitive pattern: new hires or interns are more prone to leave early.

2. Second-Level Splits: Overtime and Salary

For employees with low experience, the model checks if:

They are working overtime (a strong indicator of burnout),
And whether they have a low salary (dissatisfaction driver).

This leads to leaves that confidently predict attrition when all three conditions are met.

Example rule path:

IF Experience < 3 AND Overtime = Yes AND Salary < 50000 THEN Attrition = 1 (Left)

3. Stable Employees: Seniority + Balance

On the other branch, the tree captures experienced employees (e.g., >10 years of experience), further splitting them based on:

Work-Life Balance
Distance to Office
Education Level

A typical rule might look like:

IF Experience ≥ 10 AND WorkLifeBalance ≥ 3 AND Distance ≤ 20 THEN Attrition = 0 (Stayed)

This captures a stable cohort: seasoned professionals, well-paid, with manageable commutes and good balance.

4. Role-Specific Patterns

The tree branches also learn that:

Employees in Tech or Sales with high salaries are less likely to leave.
HR employees with poor work-life balance may be more vulnerable.

The presence of multiple one-hot-encoded department features ensures that department-based patterns are learned independently.

Visual Insights

The tree clearly visualizes:

Thresholds (e.g., Salary < 48000, Distance > 30)
Dominant features like Experience, Overtime, Salary
Class distributions in the leaves, highlighting whether most samples in a node are “Stayed” or “Left”

Each node shows:

The splitting rule
Gini impurity (or other criterion)
Number of samples reaching the node
Class distribution
Predicted class

This interpretability is the key strength of decision trees, especially in domains like HR analytics, healthcare, and credit risk.

Component	Description
Root Node	First node representing the full dataset
Internal Nodes	Feature-based decision points
Leaf Nodes	Output predictions (class or regression value)
Branches	Outcomes of feature-based decisions (edges)
Decision Paths	Complete rule chains from root to leaf
Visualization	Crucial for interpretability; tools like `plot_tree` and Graphviz help with rendering

In the next section, we’ll dive deeper into How Trees Learn to Split — covering the core algorithms (CART, ID3), and splitting criteria like Gini Impurity, Entropy, and MSE, with visualizations and decision boundaries.

3.2 Splitting Criteria: The Engine of Decision Trees

At the core of every decision tree lies the process of splitting—the mechanism that recursively partitions data into increasingly homogeneous subsets. This process is driven by a greedy algorithm that evaluates potential splits based on a chosen criterion, aiming to maximize the “purity” of resulting nodes. While finding the globally optimal tree structure is NP-hard, greedy splitting strategies, guided by carefully designed criteria, deliver robust and practical results. In this section, we’ll dive deep into the primary splitting criteria used in decision trees, covering their mathematical foundations, practical considerations, and trade-offs. Whether you’re an undergrad, an early-career data scientist, or an applied ML practitioner, this guide will equip you with the intuition and rigor to understand and apply these concepts effectively.

We’ll explore the following splitting criteria:

Gini Impurity (used in CART for classification)
Entropy and Information Gain (used in ID3/C4.5 for classification)
Gain Ratio (an enhancement in C4.5)
Variance Reduction (used in CART for regression)
Chi-Square (used in CHAID for statistical splitting)

We’ll also discuss their computational properties, biases, practical use cases, implementation tips, and additional considerations like handling continuous features, multiway splits, and stopping criteria, with mathematical derivations and real-world examples to ground the theory.

3.2.1 Gini Impurity (CART)

3.2.1.1 Definition

Gini impurity is a computationally efficient measure of node impurity used in the Classification and Regression Trees (CART) algorithm for classification tasks. It quantifies the probability of misclassifying a randomly chosen sample from a node if labeled according to the node’s class distribution. Unlike the Gini coefficient used in economics, Gini impurity is specifically designed for decision trees to measure node purity.

Given a dataset $S = \{(x_1, y_1), \ldots, (x_n, y_n)\}$ where $y_i \in \{1, \ldots, c\}$ and $c$ is the number of classes, let $S_k \subseteq S$ denote the subset of samples with label $k$, i.e., $S_k = \{(x, y) \in S : y = k\}$. The dataset is partitioned such that $S = S_1 \cup \cdots \cup S_c$. Define the proportion of samples in class $k$ as:

\[p_k = \frac{|S_k|}{|S|}\]

The Gini impurity of a node $S$ is defined as:

\[G(S) = \sum_{k=1}^c p_k (1 - p_k)\]

This can be rewritten using the identity $p_k (1 - p_k) = p_k - p_k^2$:

\[G(S) = \sum_{k=1}^c (p_k - p_k^2) = \sum_{k=1}^c p_k - \sum_{k=1}^c p_k^2 = 1 - \sum_{k=1}^c p_k^2\]

Range: $G \in [0, 1]$
- $G = 0$: Perfectly pure node (all samples belong to one class, i.e., $p_k = 1$ for one class and $p_k = 0$ for others).
- $G = 0.5$: Maximum impurity for two classes (e.g., $p_1 = p_2 = 0.5$).
- $G = 1 - \frac{1}{c}$: Maximum impurity for $c$ equally distributed classes (e.g., $p_k = \frac{1}{c}$ for all $k$).

3.2.1.2 Geometric Interpretation

Gini impurity represents the expected error if a sample is labeled randomly according to the node’s class distribution. For a two-class problem, the function $G(p) = p(1-p)$ forms a parabolic curve, reaching its maximum at $p = 0.5$, where classes are evenly split, indicating maximum uncertainty. This intuitive interpretation makes Gini a popular choice for assessing node purity.

3.2.1.3 Splitting Criterion

For a binary split creating left and right subsets $S_L$ and $S_R$ such that $S = S_L \cup S_R$ and $S_L \cap S_R = \emptyset$, with $n_L = |S_L|$ and $n_R = |S_R|$ samples respectively, the weighted Gini impurity of the tree after the split is:

\[G_T(S) = \frac{|S_L|}{|S|} G(S_L) + \frac{|S_R|}{|S|} G(S_R)\]

The split is chosen to minimize $G_T(S)$, or equivalently, to maximize the Gini reduction:

\[\Delta G = G(S) - G_T(S)\]

3.2.1.4 Example

Consider a node with 10 red (positive) and 5 blue (negative) samples ($|S| = 15$):

Parent Gini: $p_{\text{red}} = \frac{10}{15} = \frac{2}{3}, \quad p_{\text{blue}} = \frac{5}{15} = \frac{1}{3}$ $G(S) = 1 - \left( \left(\frac{2}{3}\right)^2 + \left(\frac{1}{3}\right)^2 \right) = 1 - \left( \frac{4}{9} + \frac{1}{9} \right) = 1 - \frac{5}{9} = 0.444$

Alternatively, using the Wikipedia formulation: $G(S) = p_{\text{red}}(1 - p_{\text{red}}) + p_{\text{blue}}(1 - p_{\text{blue}}) = \frac{2}{3} \cdot \frac{1}{3} + \frac{1}{3} \cdot \frac{2}{3} = \frac{2}{9} + \frac{2}{9} = \frac{4}{9} = 0.444$

Candidate Split:
- Left node: 8 red, 0 blue ($\mid S_L\mid = 8$)
- Right node: 2 red, 5 blue ($\mid S_R\mid = 7$)
Left Gini: $p_{\text{red}} = \frac{8}{8} = 1, \quad p_{\text{blue}} = \frac{0}{8} = 0$ $G(S_L) = 1 - (1^2 + 0^2) = 0$
Right Gini: $p_{\text{red}} = \frac{2}{7}, \quad p_{\text{blue}} = \frac{5}{7}$ $G(S_R) = 1 - \left( \left(\frac{2}{7}\right)^2 + \left(\frac{5}{7}\right)^2 \right) = 1 - \left( \frac{4}{49} + \frac{25}{49} \right) = 1 - \frac{29}{49} = \frac{20}{49} \approx 0.408$
Weighted Gini: $G_T(S) = \frac{8}{15} \cdot 0 + \frac{7}{15} \cdot 0.408 = 0 + 0.1904 = 0.1904$
Gini Reduction: $\Delta G = 0.444 - 0.1904 = 0.2536$

This split significantly reduces impurity, making it a strong candidate.

3.2.1.5 Properties

Computational Efficiency: Gini avoids logarithms, making it faster than entropy-based measures, as it only requires squaring and summing probabilities.
Bias: Slightly favors splits that create pure nodes for the majority class, which can be advantageous in imbalanced datasets but may overlook minority classes.
Use Case: Default in CART implementations (e.g., scikit-learn) due to speed and simplicity.
Relation to Variance: For binary classification, Gini impurity is equivalent to twice the variance of the class indicator variable, scaled by the node size, providing a probabilistic interpretation.
Practical Insight: Gini is less sensitive to class imbalance than entropy, often leading to similar splits in practice but with lower computational cost.

3.2.2 Entropy and Information Gain (ID3/C4.5)

3.2.2.1 Definition

Entropy, rooted in information theory, measures the uncertainty or randomness in a node’s class distribution. It quantifies how much information is needed to predict the class of a randomly chosen sample. For a dataset $S = \{(x_1, y_1), \ldots, (x_n, y_n)\}$ with $y_i \in \{1, \ldots, c\}$ and $c$ classes, let $p_k = \frac{|S_k|}{|S|}$ be the proportion of samples in class $k$, where $S_k = \{(x, y) \in S : y = k\}$. The entropy of a node $S$ is:

\[H(S) = - \sum_{k=1}^c p_k \log_2(p_k)\]

Range: $H \in [0, \log_2(c)]$
- $H = 0$: Perfectly pure node (all samples belong to one class, e.g., $p_k = 1$ for one $k$).
- $H = \log_2(c)$: Maximum entropy when classes are equally distributed ($p_k = \frac{1}{c}$ for all $k$), resembling a uniform distribution.

The base-2 logarithm ensures entropy is measured in bits, reflecting the information content required to encode the class distribution.

3.2.2.2 Connection to KL-Divergence

Entropy can be derived as a measure of how close the node’s class distribution $p = (p_1, \ldots, p_c)$ is to the uniform distribution $q = (q_1, \ldots, q_c)$, where $q_k = \frac{1}{c}$ for all $k$. The uniform distribution represents the worst-case scenario for classification, where each class is equally likely, and prediction reduces to random guessing. The Kullback-Leibler (KL) divergence between $p$ and $q$ quantifies this “closeness”:

\[KL(p||q) = \sum_{k=1}^c p_k \log \left( \frac{p_k}{q_k} \right)\]

Since $q_k = \frac{1}{c}$:

\[KL(p||q) = \sum_{k=1}^c p_k \log \left( \frac{p_k}{\frac{1}{c}} \right) = \sum_{k=1}^c p_k \log(p_k) - \sum_{k=1}^c p_k \log \left( \frac{1}{c} \right)\] \[= \sum_{k=1}^c p_k \log(p_k) + \sum_{k=1}^c p_k \log(c)\] \[= \sum_{k=1}^c p_k \log(p_k) + \log(c) \sum_{k=1}^c p_k\]

Since $\sum_{k=1}^c p_k = 1$:

\[KL(p||q) = \sum_{k=1}^c p_k \log(p_k) + \log(c)\]

To minimize the distance to the uniform distribution (i.e., maximize purity), we minimize $KL(p \mid \mid q)$. The term $\log(c)$ is constant, so:

$\arg\max_p KL(p||q) = \arg\max_p \sum_{k=1}^c p_k \log(p_k)$ $= \arg\min_p \left( - \sum_{k=1}^c p_k \log(p_k) \right) = \arg\min_p H(S)$

Thus, minimizing entropy $H(S)$ corresponds to maximizing the divergence from the uniform distribution, achieving a purer node.

3.2.2.3 Information Gain

Information Gain (IG) measures the reduction in entropy after a split on feature $A$:

\[IG(S, A) = H(S) - \sum_{v \in \text{values}(A)} \frac{|S_v|}{|S|} H(S_v)\]

where $S_v$ is the subset of samples with feature $A = v$, and $H(S_v)$ is the entropy of that subset. For a binary split into $S_L$ and $S_R$, the entropy of the tree is:

\[H_T(S) = \frac{|S_L|}{|S|} H(S_L) + \frac{|S_R|}{|S|} H(S_R)\]

The split maximizing $IG(S, A) = H(S) - H_T(S)$ is chosen, as it reduces uncertainty the most.

3.2.2.4 Example

Using the same node with 10 red (positive) and 5 blue (negative) samples ($|S| = 15$):

Parent Entropy: $p_{\text{red}} = \frac{2}{3}, \quad p_{\text{blue}} = \frac{1}{3}$ $H(S) = - \left( \frac{2}{3} \log_2 \left(\frac{2}{3}\right) + \frac{1}{3} \log_2 \left(\frac{1}{3}\right) \right)$ $\approx - \left( \frac{2}{3} \cdot (-0.585) + \frac{1}{3} \cdot (-1.585) \right) \approx 0.918$
Candidate Split:
- Left node: 8 red, 0 blue ($\mid S_L\mid = 8$)
- Right node: 2 red, 5 blue ($\mid S_R\mid = 7$)
Left Entropy: $H(S_L) = - \left( 1 \cdot \log_2(1) + 0 \cdot \log_2(0) \right) = 0$
Right Entropy: $p_{\text{red}} = \frac{2}{7}, \quad p_{\text{blue}} = \frac{5}{7}$ $H(S_R) = - \left( \frac{2}{7} \log_2 \left(\frac{2}{7}\right) + \frac{5}{7} \log_2 \left(\frac{5}{7}\right) \right) \approx 0.863$
Weighted Entropy: $H_T(S) = \frac{8}{15} \cdot 0 + \frac{7}{15} \cdot 0.863 \approx 0.402$
Information Gain: $IG = 0.918 - 0.402 = 0.516$

3.2.2.5 Properties

Sensitivity: Entropy is more sensitive to class imbalance than Gini, as the logarithmic function heavily penalizes small probabilities, making it effective for datasets where minority classes are critical.
Computational Cost: The logarithm calculations make entropy slower than Gini, especially for large datasets.
Use Case: Preferred in ID3 and C4.5, particularly when interpretability is key or when modeling requires sensitivity to class distributions.
Bias: Favors features with many values, as they produce more partitions with lower entropy, potentially leading to overfitting.
KL-Divergence Insight: The connection to KL-divergence provides a theoretical foundation, showing that entropy minimization pushes the class distribution away from uniform randomness, enhancing predictive power.

3.2.3 Gain Ratio (C4.5)

3.2.3.1 Motivation

Imagine you’re a chef choosing ingredients for a soup, and you pick the one that adds the most flavor. Information Gain (Section 3.2.2) works similarly, selecting features that reduce entropy the most. However, it has a flaw: it loves features with many unique values, like a customer ID or a timestamp, because they can create tiny, pure subsets—think of chopping an onion into a hundred pieces to make each “perfectly” uniform, but uselessly small. This leads to overfitting, as the tree memorizes the training data instead of generalizing. Gain Ratio, introduced in C4.5, fixes this by normalizing Information Gain to penalize features that over-fragment the data, ensuring the tree picks splits that are both informative and balanced, like choosing just the right amount of seasoning for your soup.

3.2.3.2 Split Information

To balance Information Gain, C4.5 introduces Split Information, which measures how evenly a feature splits the data. It’s like checking if your soup ingredients are distributed sensibly across portions. For a dataset $S$ with $n$ samples and a feature $A$ with values $\{v_1, v_2, \ldots, v_k\}$, where $S_v$ is the subset of samples with value $v$, Split Information is defined as:

\[\text{SplitInfo}(S, A) = - \sum_{v \in \text{values}(A)} \frac{\mid S_v\mid }{n} \log_2 \left( \frac{\mid S_v\mid }{n} \right)\]

This is the entropy of the split itself, where $\frac{\mid S_v\mid }{n}$ is the proportion of samples in subset $S_v$. A feature with many small subsets (e.g., a unique ID) has high Split Information, as the proportions are tiny and spread out, increasing the sum of $-\frac{\mid S_v\mid }{n} \log_2 \left( \frac{\mid S_v\mid }{n} \right)$. A balanced split (e.g., two equal subsets) has lower Split Information, closer to 1.0, making it more desirable.

3.2.3.3 Gain Ratio

The Gain Ratio normalizes Information Gain by dividing it by Split Information:

\[GR(S, A) = \frac{IG(S, A)}{\text{SplitInfo}(S, A)}\]

where $IG(S, A) = H(S) - \sum_{v \in \text{values}(A)} \frac{\mid S_v\mid }{n} H(S_v)$ is the Information Gain (Section 3.2.2), and $H(S) = - \sum_{k=1}^c p_k \log_2(p_k)$ is the entropy of the parent node. By dividing by Split Information, Gain Ratio penalizes splits that create many small, fragmented subsets, favoring features that balance purity and simplicity. Think of it as choosing a recipe that’s flavorful (high Information Gain) but doesn’t require chopping a hundred ingredients (high Split Information).

3.2.3.4 Example

Let’s walk through a real-world example to make this concrete. Suppose you’re building a decision tree to predict whether customers will buy a product (Yes/No) based on their “City” feature, with 15 customers: 10 say “Yes” and 5 say “No.” The parent entropy is:

\[H(S) = - \left( \frac{10}{15} \log_2 \left( \frac{10}{15} \right) + \frac{5}{15} \log_2 \left( \frac{5}{15} \right) \right) = - \left( \frac{2}{3} \cdot (-0.585) + \frac{1}{3} \cdot (-1.585) \right) \approx 0.918\]

Now, consider a split on “City” with three values: {New York, Chicago, Miami}, creating subsets:

New York: 5 Yes, 0 No → $H(S_{\text{NY}}) = 0$ (pure)
Chicago: 3 Yes, 2 No → $H(S_{\text{Chicago}}) = - \left( \frac{3}{5} \log_2 \left( \frac{3}{5} \right) + \frac{2}{5} \log_2 \left( \frac{2}{5} \right) \right) \approx 0.971$
Miami: 2 Yes, 3 No → $H(S_{\text{Miami}}) \approx 0.971$

Information Gain:

Weighted child entropy: $\frac{5}{15} \cdot 0 + \frac{5}{15} \cdot 0.971 + \frac{5}{15} \cdot 0.971 = 0.647$
\[IG(S, \text{City}) = H(S) - \sum \frac{|S_v|}{n} H(S_v) = 0.918 - 0.647 \approx 0.271\]

Split Information:

Proportions: $\frac{\mid S_{\text{NY}}\mid }{n} = \frac{5}{15} = \frac{1}{3}$, similarly for Chicago and Miami.
\[\text{SplitInfo}(S, \text{City}) = - \left( \frac{5}{15} \log_2 \left( \frac{5}{15} \right) + \frac{5}{15} \log_2 \left( \frac{5}{15} \right) + \frac{5}{15} \log_2 \left( \frac{5}{15} \right) \right) = - 3 \cdot \frac{1}{3} \cdot (-1.585) \approx 1.585\]

Gain Ratio:

\[GR(S, \text{City}) = \frac{IG(S, \text{City})}{\text{SplitInfo}(S, \text{City})} = \frac{0.271}{1.585} \approx 0.171\]

Now, compare this to a high-cardinality feature like “Customer ID” with 15 unique values, each with one sample. Its Split Information would be:

\[\text{SplitInfo}(S, \text{ID}) = - \sum_{i=1}^{15} \frac{1}{15} \log_2 \left( \frac{1}{15} \right) = - 15 \cdot \frac{1}{15} \cdot (-3.907) \approx 3.907\]

Even if “Customer ID” yields a high Information Gain (e.g., 0.918 for pure leaves), its Gain Ratio is lower ($\frac{0.918}{3.907} \approx 0.235$), so “City” might be preferred if its Gain Ratio is competitive after evaluating other features.

3.2.3.5 Properties

Bias Correction: Gain Ratio reduces Information Gain’s bias toward high-cardinality features by penalizing splits with high Split Information, ensuring more generalizable trees.
Use Case: Essential in C4.5 for datasets with categorical features like customer demographics or product categories, where high-cardinality features are common.
Caveat: If Split Information is near zero (e.g., one subset contains almost all samples), Gain Ratio becomes unstable (division by near-zero). C4.5 includes guardrails, like minimum subset sizes, to prevent this.
Practical Tip: Use Gain Ratio when dealing with categorical features with varying numbers of values, but monitor for imbalanced splits and validate with cross-validation to ensure robust performance.

3.2.4 Variance Reduction (Regression Trees)

3.2.4.1 Definition

In regression trees, the goal is to predict a continuous target variable, like house prices or temperature, rather than a class label. Instead of minimizing impurity (e.g., Gini or entropy), we minimize the variance of the target values within each node, ensuring that samples in a leaf are as similar as possible. Think of it as grouping similar temperatures in a weather prediction model so each leaf predicts a tight range, like “around 75°F.” The variance of a node $S$ with target values $\{y_1, y_2, \ldots, y_n\}$ is:

\[\text{Var}(S) = \frac{1}{\mid S\mid } \sum_{i \in S} (y_i - \bar{y})^2\]

where $\bar{y} = \frac{1}{\mid S\mid } \sum_{i \in S} y_i$ is the mean target value in the node, and $\mid S\mid$ is the number of samples. This is the sample variance, measuring how spread out the target values are around their mean.

3.2.4.2 Variance Reduction

When splitting a node into left and right children ($S_L$ and $S_R$), the tree selects the feature and threshold that maximize Variance Reduction, which measures how much the split reduces the overall variance. The formula is:

\[\Delta \text{Var}(S, A, t) = \text{Var}(S) - \left( \frac{\mid S_L\mid }{\mid S\mid } \text{Var}(S_L) + \frac{\mid S_R\mid }{\mid S\mid } \text{Var}(S_R) \right)\]

Here, $A$ is the feature, $t$ is the threshold (for continuous features) or category partition (for categorical), $S_L = \{i \in S : A_i \leq t\}$ (or $A_i \in \text{subset}_L$), and $S_R = S \setminus S_L$. The weighted average of the child variances accounts for the proportion of samples in each child, ensuring fair comparison across splits. A high $\Delta \text{Var}$ means the split creates children with tightly clustered target values, improving prediction accuracy.

3.2.4.3 Example

Let’s predict house prices based on square footage, with a node containing 5 houses: $y = [200, 220, 240, 260, 280]$ (in thousands of dollars). The mean is:

\[\bar{y} = \frac{200 + 220 + 240 + 260 + 280}{5} = 240\]

Parent Variance:

Deviations: $(200-240)^2 = 1600$, $(220-240)^2 = 400$, $(240-240)^2 = 0$, $(260-240)^2 = 400$, $(280-240)^2 = 1600$
\[\text{Var}(S) = \frac{1600 + 400 + 0 + 400 + 1600}{5} = \frac{4000}{5} = 800\]

Suppose we split on “Square Footage < 1500 sq ft,” creating:

Left Child ($S_L$): $[200, 220]$, mean $\bar{y}_L = \frac{200 + 220}{2} = 210$
Right Child ($S_R$): $[240, 260, 280]$, mean $\bar{y}_R = \frac{240 + 260 + 280}{3} = 260$

Left Variance:

Deviations: $(200-210)^2 = 100$, $(220-210)^2 = 100$
\[\text{Var}(S_L) = \frac{100 + 100}{2} = 100\]

Right Variance:

Deviations: $(240-260)^2 = 400$, $(260-260)^2 = 0$, $(280-260)^2 = 400$
\[\text{Var}(S_R) = \frac{400 + 0 + 400}{3} = \frac{800}{3} \approx 266.667\]

Weighted Child Variance:

Proportions: $\mid S_L\mid = 2$, $\mid S_R\mid = 3$, $\mid S\mid = 5$
\[\text{Var}_{\text{split}} = \frac{2}{5} \cdot 100 + \frac{3}{5} \cdot 266.667 = 40 + 160 \approx 200\]

Variance Reduction:

\[\Delta \text{Var} = 800 - 200 = 600\]

The tree evaluates all possible thresholds (e.g., Square Footage < 1400, 1600, etc.) and selects the one maximizing $\Delta \text{Var}$. In this case, a reduction of 600 indicates a strong split, as the child nodes have much tighter price ranges.

3.2.4.4 Properties

Intuitive: Variance Reduction minimizes the spread of target values, ensuring each leaf predicts a value close to its samples’ mean, like forecasting a consistent temperature for a region.
Use Case: Standard in CART for regression tasks, such as predicting prices, temperatures, or sales.
Relation to MSE: Minimizing weighted child variance is equivalent to minimizing the mean squared error (MSE) of predictions, since $\text{Var}(S) = \frac{1}{\mid S\mid } \sum_{i \in S} (y_i - \bar{y})^2$ is the MSE when predicting $\bar{y}$.
Limitation: Only applicable to continuous targets, not classification. For categorical targets, use Gini or entropy (Sections 3.2.1, 3.2.2).
Practical Tip: For regression tasks, monitor Variance Reduction during tree growth to ensure splits are meaningful. Use cross-validation to avoid overfitting by limiting tree depth (Section 3.5).

3.2.5 Chi-Square Splitting (CHAID)

3.2.5.1 Approach

Imagine you’re a marketing analyst segmenting customers into groups based on their purchase behavior. You want splits that create meaningful, statistically significant groups, not just random divisions. The Chi-Square Automatic Interaction Detector (CHAID) algorithm uses the chi-square test to evaluate whether a feature’s split produces subsets with significantly different class distributions. Unlike Gini or entropy, which focus on purity, CHAID ensures splits are statistically justified, making it ideal for interpretable applications like market research or social sciences, where you need to explain why a split matters (e.g., “Age groups differ significantly in buying patterns”).

3.2.5.2 Chi-Square Statistic

CHAID assesses splits using the chi-square test of independence, which checks if the class distribution in each subset differs significantly from what we’d expect if the feature and target were independent. For a feature $A$ with values $\{v_1, v_2, \ldots, v_k\}$ and classes $\{c_1, c_2, \ldots, c_m\}$, the chi-square statistic is:

\[\chi^2 = \sum_{k=1}^m \sum_{v=1}^k \frac{(O_{k,v} - E_{k,v})^2}{E_{k,v}}\]

where:

$O_{k,v}$: Observed count of class $k$ in subset $v$ (e.g., number of “Yes” customers in “New York”).
$E_{k,v}$: Expected count under independence, calculated as: $E_{k,v} = \frac{(\text{Total samples in subset } v) \cdot (\text{Total samples of class } k)}{\text{Total samples } n}$
The test compares observed and expected counts, yielding a p-value. A low p-value (e.g., < 0.05) indicates the split significantly separates classes.

CHAID also merges categories with similar class distributions (based on high p-values) before splitting, reducing the number of branches and enhancing interpretability.

3.2.5.3 Example

Suppose you’re predicting customer purchases (Yes/No) based on “Age Group” {Young, Middle, Senior} with 30 customers: 15 Yes, 15 No. The contingency table is:

Age Group	Yes	No	Total
Young	8	2	10
Middle	5	5	10
Senior	2	8	10
Total	15	15	30

Step 1: Compute Expected Counts:

For Young, Yes: $E_{\text{Young,Yes}} = \frac{10 \cdot 15}{30} = 5$
Similarly, $E_{\text{Young,No}} = 5$, $E_{\text{Middle,Yes}} = 5$, $E_{\text{Middle,No}} = 5$, $E_{\text{Senior,Yes}} = 5$, $E_{\text{Senior,No}} = 5$.

Step 2: Chi-Square Statistic:

For each cell: $\frac{(O_{k,v} - E_{k,v})^2}{E_{k,v}}$
- Young, Yes: $\frac{(8-5)^2}{5} = \frac{9}{5} = 1.8$
- Young, No: $\frac{(2-5)^2}{5} = \frac{9}{5} = 1.8$
- Middle, Yes: $\frac{(5-5)^2}{5} = 0$
- Middle, No: $\frac{(5-5)^2}{5} = 0$
- Senior, Yes: $\frac{(2-5)^2}{5} = \frac{9}{5} = 1.8$
- Senior, No: $\frac{(8-5)^2}{5} = \frac{9}{5} = 1.8$
Total: $\chi^2 = 1.8 + 1.8 + 0 + 0 + 1.8 + 1.8 = 7.2$

Step 3: Evaluate Significance:

With 2 degrees of freedom ($(3-1) \cdot (2-1) = 2$), a $\chi^2 = 7.2$ yields a p-value of approximately 0.027 (using a chi-square table), suggesting a significant split (p < 0.05).

Step 4: Merging:

If Middle and Senior had similar class distributions (e.g., both 5 Yes, 5 No), CHAID would test merging them (via another chi-square test) to reduce branches, creating a split like “Young vs. Middle/Senior.”

3.2.5.4 Properties

Advantages:
- Statistical Rigor: P-values ensure splits are meaningful, enhancing trust in fields like marketing or social sciences.
- Multiway Splits: Unlike CART’s binary splits, CHAID’s multiway splits (e.g., one branch per age group) are intuitive for categorical data.
- Interpretability: Merged categories and p-values make results easy to explain (e.g., “Young customers are significantly more likely to buy”).
Limitations:
- Sample Size: Chi-square tests require large samples for reliable p-values, limiting CHAID’s use with small datasets.
- Computational Cost: Calculating chi-square statistics and merging categories is more intensive than Gini or entropy.
- Categorical Focus: Continuous features must be binned, potentially losing information (Section 3.4.1).
Practical Tip: Use CHAID for interpretable tasks with categorical data and sufficient samples, like customer segmentation. Validate p-value thresholds (e.g., 0.05) to balance significance and tree size.

3.2.6 Handling Continuous Features

3.2.6.1 Thresholding Continuous Features

For continuous features, decision trees evaluate splits by selecting a threshold $t$ and partitioning the data into $\{ x_i \leq t \}$ and $\{ x_i > t \}$. To find the optimal threshold:

Sort the feature values: Arrange the feature’s values in ascending order.
Evaluate candidate thresholds: Typically, thresholds are chosen as midpoints between consecutive unique values to reduce computational cost.
Compute impurity reduction: For each candidate threshold, calculate the impurity (e.g., Gini, entropy) or variance reduction and select the threshold maximizing the reduction.

For a feature with $n$ unique values, evaluating all midpoints requires $O(n \log n)$ time for sorting and $O(n)$ for impurity calculations.

3.2.6.2 Example

For a continuous feature $x = [1.1, 1.5, 2.0, 2.5, 3.0]$ with corresponding labels $[0, 0, 1, 1, 1]$, possible thresholds are midpoints like $1.3, 1.75, 2.25, 2.75$. The algorithm evaluates the impurity reduction for each and selects the best.

3.2.7 Multiway Splits vs. Binary Splits

3.2.7.1 Multiway Splits

Algorithms like ID3 and CHAID allow multiway splits, where a categorical feature with $k$ values creates $k$ child nodes. This is intuitive for categorical data but can lead to:

Overly fragmented trees: Many small nodes increase overfitting risk.
High computational cost: Evaluating multiway splits is more expensive, especially for high-cardinality features.

3.2.7.2 Binary Splits

CART uses binary splits, even for categorical features, by grouping values into two subsets. This:

Simplifies tree structure.
Reduces computational complexity, as there are $2^{k-1} - 1$ possible binary partitions for $k$ categories, but efficient algorithms reduce this to $O(k)$.
May require multiple splits to achieve the same separation as a single multiway split.

3.2.7.3 Practical Choice

Use binary splits (CART) for computational efficiency.
Use multiway splits (CHAID, ID3) for interpretability or when categorical features suggest multiple branches.

3.2.8 Comparative Overview

Criterion	Use Case	Pros	Cons
Gini Impurity	Classification	Fast, default in CART, robust	Slightly favors majority class splits
Entropy/IG	Classification	Intuitive, sensitive to imbalance	Slower, biased toward high-cardinality
Gain Ratio	Classification	Corrects IG bias	Sensitive to imbalanced splits
Variance Reduction	Regression	Natural for continuous targets	Limited to numeric targets
Chi-Square	Classification	Statistical rigor, multiway splits	Requires large samples, computationally heavy

3.2.9 Practical Tips

Choose Gini for Speed: Use Gini for large datasets or when computational efficiency is critical (e.g., scikit-learn’s default).
Use Entropy for Interpretability: Entropy and Information Gain provide a clear information-theoretic perspective, ideal for teaching or explaining models.
Handle High-Cardinality Features: Use Gain Ratio in C4.5 for datasets with categorical features having many unique values.
Regression? Variance Reduction: Always use variance reduction for regression tasks—it’s intuitive and effective.
Statistical Rigor with CHAID: Opt for chi-square splits in domains requiring statistical significance.
Mitigate Overfitting: Use hyperparameters like min_samples_leaf, max_depth, or min_impurity_decrease. Post-pruning is also effective.
Combine with Ensembles: Decision trees are prone to high variance. Use Random Forests or Gradient Boosting for robustness.
Handle Continuous Features Efficiently: Sort feature values once per node to evaluate thresholds.
Consider Multiway Splits Sparingly: Reserve multiway splits for interpretable models or small datasets.

3.3 Classic Decision Tree Algorithms

Decision tree algorithms are the backbone of many machine learning applications, transforming raw data into interpretable, hierarchical models through recursive splitting. Each algorithm implements the splitting criteria discussed in Section 3.2 (e.g., Gini impurity, entropy, variance reduction) with unique characteristics, optimizations, and trade-offs. This section explores the four classic decision tree algorithms—ID3, C4.5, CART, and CHAID—detailing their mechanisms, mathematical foundations, strengths, limitations, and practical use cases. We’ll also analyze their computational complexity, scalability, and suitability for different data types, ensuring you have the knowledge to select the right algorithm for your task. Whether you’re building a model for classification, regression, or interpretable analytics, this guide will provide the rigor and intuition needed to navigate these algorithms effectively.

We’ll cover the following algorithms:

ID3 (Iterative Dichotomiser 3): Focuses on categorical data and information gain.
C4.5: Extends ID3 with continuous data handling, missing value strategies, and gain ratio.
CART (Classification and Regression Trees): Uses binary splits for both classification and regression.
CHAID (Chi-Square Automatic Interaction Detector): Employs chi-square tests for multiway splits.

We’ll conclude with a comparative analysis of their trade-offs in complexity, scalability, and use cases, enriched with practical examples and implementation tips.

3.3.1 ID3 (Iterative Dichotomiser 3)

3.3.1.1 Overview

Developed by Ross Quinlan, ID3 (Iterative Dichotomiser 3) is one of the earliest decision tree algorithms, designed primarily for classification tasks with categorical features. It uses information gain based on entropy to select splits, aiming to maximize the reduction in uncertainty at each node. While pioneering, ID3 is primarily a teaching tool today due to its limitations in handling continuous features, missing values, and overfitting.

3.3.1.2 Mechanism

ID3 operates by recursively partitioning the dataset $S = \{(x_1, y_1), \ldots, (x_n, y_n)\}$, where $y_i \in \{1, \ldots, c\}$ represents class labels, into homogeneous subsets. The algorithm follows these steps:

Base Cases:
- If all samples in $S$ have the same label, return a leaf node with that label.
- If no features remain or other stopping criteria are met (e.g., minimum node size), return a leaf with the majority class.
Split Selection:
- Compute the entropy of the current node: $H(S) = - \sum_{k=1}^c p_k \log_2(p_k), \quad p_k = \frac{|S_k|}{|S|}, \quad S_k = \{(x, y) \in S : y = k\}$
- For each feature $A$, compute the information gain: $IG(S, A) = H(S) - \sum_{v \in \text{values}(A)} \frac{|S_v|}{|S|} H(S_v)$
- Select the feature $A$ that maximizes $IG(S, A)$.
Recursion:
- Create a child node for each value $v$ of the selected feature and recurse on the subset $S_v$.

ID3 produces multiway splits for categorical features, creating one branch per unique value, which can lead to compact but potentially overfitted trees.

3.3.1.3 Limitations

Categorical Features Only: ID3 natively handles only categorical features. Continuous features must be discretized beforehand (e.g., by binning), which can lead to information loss or arbitrary thresholds.
No Pruning: ID3 grows trees until leaves are pure or meet a minimum size, often resulting in overfitting, especially on noisy datasets.
No Missing Value Handling: ID3 assumes complete data, requiring preprocessing to impute missing values.
Bias Toward High-Cardinality Features: Information gain favors features with many values, as they produce more partitions, potentially leading to impractical trees.

3.3.1.4 Example

Consider a dataset with 15 samples (10 red, 5 blue) and a categorical feature $A$ with three values ($v_1, v_2, v_3$):

Subset $S_{v_1}$: 5 red, 0 blue → $H(S_{v_1}) = 0$
Subset $S_{v_2}$: 3 red, 2 blue → $H(S_{v_2}) \approx 0.971$
Subset $S_{v_3}$: 2 red, 3 blue → $H(S_{v_3}) \approx 0.971$
Parent entropy: $H(S) \approx 0.918$
Information gain: $IG(S, A) = 0.918 - \left( \frac{5}{15} \cdot 0 + \frac{5}{15} \cdot 0.971 + \frac{5}{15} \cdot 0.971 \right) \approx 0.918 - 0.647 \approx 0.271$ ID3 selects $A$ if it maximizes information gain and creates three branches.

3.3.1.5 Properties

Strengths: Simple, interpretable, and effective for small, clean datasets with categorical features.
Weaknesses: Prone to overfitting, limited to categorical data, and lacks robust missing value handling.
Use Case: Primarily academic or for datasets with purely categorical features and low noise.

3.3.2 C4.5

3.3.2.1 Overview

C4.5, also developed by Quinlan, is a robust successor to ID3, addressing its limitations by introducing support for continuous features, missing value handling, and pruning. It uses gain ratio to mitigate ID3’s bias toward high-cardinality features and is the foundation for the open-source J48 algorithm in tools like Weka.

3.3.2.2 Mechanism

C4.5 extends ID3 with the following enhancements:

Continuous Features:
- For a continuous feature, C4.5 sorts values and evaluates thresholds (midpoints between consecutive unique values) to create binary splits. The threshold maximizing information gain is chosen.
- Complexity: Sorting requires $O(n \log n)$ time, followed by $O(n)$ impurity calculations.
Gain Ratio:
- To address ID3’s bias, C4.5 uses: $GR(S, A) = \frac{IG(S, A)}{\text{SplitInfo}(S, A)}, \quad \text{SplitInfo}(S, A) = - \sum_{v \in \text{values}(A)} \frac{|S_v|}{|S|} \log_2 \left( \frac{|S_v|}{|S|} \right)$
- SplitInfo penalizes splits with many small partitions, favoring balanced splits.
Missing Values:
- C4.5 handles missing values by:
  - Probabilistic Assignment: Distribute samples with missing values across child nodes based on the observed distribution of non-missing values, weighted by probabilities.
  - Surrogate Splits: Use alternative features that mimic the primary split’s behavior.
Pruning:
- C4.5 employs pessimistic pruning, which estimates error rates on training data and removes branches that do not significantly improve accuracy, using a complexity parameter to balance tree size and performance.

3.3.2.3 Example

For a continuous feature $x = [1.1, 1.5, 2.0, 2.5, 3.0]$ with labels $[0, 0, 1, 1, 1]$:

Candidate thresholds: $1.3, 1.75, 2.25, 2.75$
Evaluate $IG(S, x \leq t)$ for each threshold, selecting the one maximizing gain ratio.
For missing values, assign a sample to child nodes with weights proportional to $$ S_v / S $$.

3.3.2.4 Properties

Strengths: Handles continuous and categorical features, mitigates overfitting via pruning, and supports missing values.
Weaknesses: Gain ratio can be unstable for highly imbalanced splits, and pruning requires careful tuning.
Use Case: Widely used in academic and data mining contexts (e.g., Weka’s J48) for mixed data types.

3.3.3 CART (Classification and Regression Trees)

3.3.3.1 Overview

Developed by Breiman et al., CART (Classification and Regression Trees) is a versatile algorithm supporting both classification and regression. It uses Gini impurity for classification and variance reduction for regression, exclusively producing binary splits for simplicity and computational efficiency.

3.3.3.2 Mechanism

CART follows these steps:

Split Selection:
- For classification, minimize Gini impurity: $G(S) = \sum_{k=1}^c p_k (1 - p_k) = 1 - \sum_{k=1}^c p_k^2, \quad p_k = \frac{|S_k|}{|S|}$ $G_T(S) = \frac{|S_L|}{|S|} G(S_L) + \frac{|S_R|}{|S|} G(S_R)$
- For regression, maximize variance reduction: $\text{Var}(S) = \frac{1}{|S|} \sum_{i \in S} (y_i - \bar{y})^2$ $\Delta \text{Var} = \text{Var}(S) - \left( \frac{|S_L|}{|S|} \text{Var}(S_L) + \frac{|S_R|}{|S|} \text{Var}(S_R) \right)$
- Evaluate all possible binary splits (feature and threshold for continuous features, or partitions for categorical features).
Binary Splits:
- For categorical features with $k$ values, CART evaluates $2^{k-1} - 1$ possible binary partitions, optimized to $O(k)$ with greedy search.
- For continuous features, sort values ($O(n \log n)$) and test midpoints.
Missing Values:
- CART uses surrogate splits: If the primary split feature is missing, it selects an alternative feature whose split closely mimics the primary split’s outcome.
Pruning:
- CART employs cost-complexity pruning, minimizing a cost function: $R_\alpha(T) = R(T) + \alpha |T|$ where $R(T)$ is the tree’s error (e.g., misclassification rate or MSE), $|T|$ is the number of leaves, and $\alpha$ is a complexity parameter tuned via cross-validation.

3.3.3.3 Example

For classification with 10 red, 5 blue samples:

Parent Gini: $G(S) = 1 - \left( \left(\frac{2}{3}\right)^2 + \left(\frac{1}{3}\right)^2 \right) = 0.444$
Split (e.g., $x \leq t$): Left (8 red, 0 blue), Right (2 red, 5 blue)
Weighted Gini: $G_T(S) = \frac{8}{15} \cdot 0 + \frac{7}{15} \cdot 0.408 \approx 0.1904$
Gini reduction: $\Delta G = 0.444 - 0.1904 = 0.2536$

3.3.3.4 Properties

Strengths: Supports classification and regression, computationally efficient, robust pruning, and effective missing value handling.
Weaknesses: Binary splits may lead to deeper trees for categorical features with many values.
Use Case: Default in modern libraries (e.g., scikit-learn’s DecisionTreeClassifier/Regressor) due to versatility and performance.

3.3.4 CHAID (Chi-Square Automatic Interaction Detector)

3.3.4.1 Overview

CHAID (Chi-Square Automatic Interaction Detector) is designed for categorical data and uses chi-square tests to evaluate splits, making it ideal for interpretable models in fields like marketing and social sciences. It supports multiway splits and stops splitting based on statistical significance.

3.3.4.2 Mechanism

CHAID operates as follows:

Split Selection:
- For each feature, perform a chi-square test of independence between the feature’s categories and the target classes: $\chi^2 = \sum_{k} \sum_{v} \frac{(O_{k,v} - E_{k,v})^2}{E_{k,v}}$ where $O_{k,v}$ is the observed count of class $k$ in category $v$, and $E_{k,v}$ is the expected count under independence.
- Merge categories with statistically insignificant differences (based on p-values) to reduce cardinality.
- Select the feature with the lowest p-value (highest significance).
Multiway Splits:
- Create one branch per (merged) category, unlike CART’s binary splits.
Stopping Criteria:
- Stop splitting if no feature provides a significant improvement (e.g., p-value below a threshold, typically 0.05).
- Ensures interpretable, statistically valid splits.
Continuous Features:
- Bin continuous features into discrete categories before applying chi-square tests.

3.3.4.3 Example

For a feature with categories $v_1, v_2, v_3$ and classes red/blue:

Compute $\chi^2$ for the contingency table of category vs. class.
Merge categories (e.g., $v_2$ and $v_3$) if their class distributions are not significantly different.
Split on the feature if the p-value is below 0.05, creating branches for each (merged) category.

3.3.4.4 Properties

Strengths: Produces interpretable multiway splits, statistically rigorous, and stops early to avoid overfitting.
Weaknesses: Requires large sample sizes for valid chi-square tests, computationally intensive, and less suited for regression.
Use Case: Ideal for marketing (e.g., customer segmentation) and social sciences where interpretability is critical.

3.3.5 Algorithm Trade-offs

3.3.5.1 Complexity

ID3: $O(mn \cdot \mid \text{values}(A)\mid )$ for $m$ features, $n$ samples, and feature $A$’s cardinality, due to multiway splits. High for high-cardinality features.
C4.5: Similar to ID3 but adds $O(n \log n)$ for continuous feature sorting. Pruning adds overhead but improves generalization.
CART: $O(mn \log n)$ due to sorting for continuous features and binary splits. Efficient for categorical features with greedy partitioning ($O(k)$ per feature).
CHAID: High complexity due to chi-square tests and category merging, especially for large datasets or high-cardinality features.

3.3.5.2 Scalability

ID3: Scales poorly for large datasets or high-cardinality features due to multiway splits and lack of pruning.
C4.5: Better scalability with pruning and continuous feature handling, but gain ratio calculations increase cost.
CART: Highly scalable due to binary splits and efficient pruning, making it the default in modern libraries.
CHAID: Less scalable for large datasets due to statistical testing and multiway splits, but effective for smaller, interpretable tasks.

3.3.5.3 Use Cases

ID3: Academic settings, small categorical datasets, or prototyping.
C4.5: Mixed data types (categorical and continuous), academic research, or tools like Weka.
CART: General-purpose classification and regression, production systems (e.g., scikit-learn), ensemble methods like Random Forests.
CHAID: Marketing, social sciences, or applications requiring interpretable multiway splits.

3.3.5.4 Comparative Table

Algorithm	Split Criterion	Split Type	Feature Types	Missing Values	Pruning	Use Case
ID3	Entropy/IG	Multiway	Categorical	None	None	Academic, categorical data
C4.5	Gain Ratio	Multiway/Binary	Categorical, Continuous	Probabilistic, Surrogate	Pessimistic	Mixed data, research
CART	Gini (Class.), Variance (Reg.)	Binary	Categorical, Continuous	Surrogate	Cost-Complexity	Production, ensembles
CHAID	Chi-Square	Multiway	Categorical (Continuous via binning)	None	Significance-based	Marketing, social sciences

3.3.6 Practical Tips

Choose CART for Production: Use CART for its scalability, support for regression, and integration with modern libraries like scikit-learn.
Use C4.5 for Mixed Data: Opt for C4.5 (or J48) when handling datasets with both categorical and continuous features, especially in academic or data mining contexts.
Reserve ID3 for Teaching: ID3 is best for understanding decision tree fundamentals but avoid it in practice due to overfitting.
Apply CHAID for Interpretability: Use CHAID in domains like marketing where multiway splits and statistical rigor enhance interpretability.
Handle Missing Values: Leverage C4.5 or CART’s robust missing value strategies to avoid extensive preprocessing.
Mitigate Overfitting: Always apply pruning (C4.5’s pessimistic pruning or CART’s cost-complexity pruning) or use ensembles like Random Forests.
Optimize for Scalability: Prefer CART for large datasets due to its binary splits and efficient implementation.

Classic decision tree algorithms—ID3, C4.5, CART, and CHAID—offer diverse approaches to building interpretable and effective models:

ID3: Simple, entropy-based, but limited to categorical data and prone to overfitting.
C4.5: Robust, handles mixed data types, uses gain ratio, and includes pruning.
CART: Versatile, scalable, supports classification and regression with binary splits.
CHAID: Interpretable, statistically rigorous, ideal for multiway splits in marketing.

Understanding their mechanisms and trade-offs allows you to select the best algorithm for your data and task. For modern applications, CART’s simplicity and integration with ensembles make it a go-to choice, while C4.5 and CHAID shine in specific contexts requiring interpretability or mixed data handling.

3.4 Handling Data Challenges

Real-world datasets are rarely clean or perfectly structured, presenting challenges like continuous and categorical features, missing values, and imbalanced class distributions. Decision trees are robust to these issues compared to other models (e.g., logistic regression), but their performance can degrade without proper handling. This section explores strategies to address these challenges, focusing on continuous versus categorical feature processing, missing value management, and techniques for imbalanced datasets. We’ll provide mathematical foundations, practical examples, and implementation tips, drawing on the algorithms discussed in Section 3.3 (ID3, C4.5, CART, CHAID). By mastering these techniques, you’ll be equipped to preprocess data effectively and build robust decision tree models for diverse applications.

We’ll cover the following challenges and solutions:

Continuous vs. Categorical Features: Discretization, binning, and optimal thresholding.
Missing Values: Surrogate splits, probabilistic assignment, and imputation.
Imbalanced Datasets: Class weighting, stratified sampling, and modified splitting criteria.

3.4.1 Continuous vs. Categorical Features

3.4.1.1 Overview

Decision trees handle both continuous and categorical features, but each requires specific strategies to optimize splits. Continuous features (e.g., temperature, age) are typically split using thresholds, while categorical features (e.g., color, city) may involve multiway or binary splits depending on the algorithm. Mishandling these can lead to overfitting, especially for high-cardinality categorical features or poorly chosen thresholds for continuous ones.

3.4.1.2 Continuous Features

For continuous features, decision trees (e.g., C4.5, CART) search for an optimal threshold $t$ to partition the data into two subsets: $\{x_i \leq t\}$ and $\{x_i > t\}$. The process is:

Sort Feature Values: Arrange the feature’s values in ascending order ($O(n \log n)$ complexity for $n$ samples).
Evaluate Thresholds: Test midpoints between consecutive unique values as candidate thresholds to reduce computational cost.
Maximize Impurity Reduction: Compute the impurity reduction (e.g., Gini, entropy, or variance) for each threshold:
- For classification: $\Delta G = G(S) - \left( \frac{\mid S_L\mid }{\mid S\mid } G(S_L) + \frac{\mid S_R\mid }{\mid S\mid } G(S_R) \right)$
- For regression: $\Delta \text{Var} = \text{Var}(S) - \left( \frac{\mid S_L\mid }{\mid S\mid } \text{Var}(S_L) + \frac{\mid S_R\mid }{\mid S\mid } \text{Var}(S_R) \right)$
- Select the threshold maximizing the reduction.

Example: For a feature $x = [1.1, 1.5, 2.0, 2.5, 3.0]$ with labels $[0, 0, 1, 1, 1]$:

Candidate thresholds: $1.3, 1.75, 2.25, 2.75$.
Evaluate $\Delta G$ or $\Delta \text{Var}$ for each threshold, choosing the best (e.g., $x \leq 1.75$ splits into $[0, 0]$ and $[1, 1, 1]$).

3.4.1.3 Categorical Features

Categorical features are handled differently based on the algorithm:

ID3/C4.5: Create multiway splits, with one branch per unique category. For a feature with $k$ values, this produces $k$ child nodes, which is intuitive but can lead to overfitting for high-cardinality features (e.g., customer IDs).
CART: Uses binary splits by partitioning categories into two subsets (e.g., for colors {Red, Green, Blue}, split into {Red, Blue} vs. {Green}). This requires evaluating $2^{k-1} - 1$ partitions, optimized to $O(k)$ with greedy algorithms.
CHAID: Merges categories with statistically similar class distributions using chi-square tests: $\chi^2 = \sum_{k} \sum_{v} \frac{(O_{k,v} - E_{k,v})^2}{E_{k,v}}$ Categories with insignificant differences (high p-values) are combined, reducing the number of branches.

Ordinal vs. Nominal: For ordinal categories (e.g., {Low, Medium, High}), order can be leveraged to treat them as continuous thresholds. For nominal categories, one-hot encoding is an option, but it increases dimensionality and risks overfitting. Advanced methods like target encoding (replacing categories with class-conditional means) or algorithms like CatBoost (which natively handle categoricals) can improve performance, though these are typically used in ensemble methods.

Discretization and Binning: For algorithms like ID3 that only handle categorical features, continuous features must be discretized:

Equal-Width Binning: Divide the feature range into fixed intervals.
Equal-Frequency Binning: Ensure each bin contains roughly the same number of samples.
Optimal Binning: Use clustering or impurity-based methods to find thresholds that maximize split quality. Discretization can lose information, so C4.5 or CART’s threshold-based approach is preferred when possible.

3.4.1.4 Properties

Continuous Features: Thresholding is computationally efficient ($O(n \log n)$) and preserves information, but poorly chosen thresholds can reduce split quality.
Categorical Features: Multiway splits (ID3, C4.5, CHAID) are interpretable but risk overfitting for high-cardinality features. Binary splits (CART) are simpler but may require deeper trees.
Practical Tip: Avoid one-hot encoding high-cardinality features; use target encoding or algorithms with native categorical support for better performance.

3.4.2 Missing Values

3.4.2.1 Overview

Missing values are common in real-world data and can disrupt decision tree training and prediction. Decision trees offer robust strategies to handle missing values without requiring extensive preprocessing, unlike many other models.

3.4.2.2 Strategies

Treat Missing as a Category:
- Assign missing values to a special “missing” category, allowing the tree to learn patterns in missingness. This is simple but may introduce bias if missingness is not informative.
- Used in C4.5 for categorical features.
Surrogate Splits (CART):
- For a sample with a missing value in the primary split feature, CART uses a surrogate split: an alternative feature whose split most closely mimics the primary split’s outcome.
- During training, compute correlation between the primary split and other features’ splits, selecting the top surrogates (e.g., based on impurity reduction).
- Example: If the primary split is “Age ≤ 30” and Age is missing, use “Income ≤ 50k” if it approximates the same partitioning.
Probabilistic Assignment (C4.5):
- During training, C4.5 distributes a sample with a missing value across all child nodes, weighted by the proportion of non-missing samples in each node: $w_v = \frac{|S_v|}{|S|}, \quad \sum_v w_v = 1$ where $S_v$ is the subset for value $v$ of the split feature.
- During prediction, average the predictions from all branches, weighted by these proportions.
- Example: For a node with two branches (80% and 20% of samples), a missing-value sample is assigned 0.8 weight to the first branch and 0.2 to the second.
Imputation:
- Preprocess the data by imputing missing values with the mean, median, or a predictive model. This is simple but may introduce bias, especially if missingness is not random (MNAR).
- Add a boolean indicator (e.g., “is_missing_FeatureX”) to capture whether missingness is informative, allowing the tree to learn patterns.

3.4.2.3 Example

For a node with a split on feature $A$ (values $v_1, v_2$) and 15 samples (10 with $v_1$, 5 with $v_2$):

A sample with missing $A$ is assigned weights $w_{v_1} = \frac{10}{15} = 0.667$, $w_{v_2} = \frac{5}{15} = 0.333$ in C4.5.
In CART, if $A$ is missing, a surrogate split (e.g., on feature $B$) routes the sample based on the best alternative rule.

3.4.2.4 Properties

Surrogate Splits (CART): Robust and preserves split logic but requires additional computation to identify surrogates.
Probabilistic Assignment (C4.5): Flexible but increases training complexity and may dilute predictive power for frequent missingness.
Imputation: Simple but risks bias; use with caution and consider missingness indicators.
Practical Tip: Analyze why data is missing (random, at random, or not at random) to choose the best strategy. Surrogate splits or probabilistic assignment are preferred for robustness.

3.4.3 Imbalanced Datasets

3.4.3.1 Overview

Imbalanced datasets, where one class significantly outnumbers others (e.g., 95% negative, 5% positive), can bias decision trees toward the majority class, as splits isolating the minority class may yield small impurity reductions. This section explores techniques to mitigate this bias, ensuring fair and effective models.

3.4.3.2 Strategies

Class Weighting:
- Assign higher weights to minority class samples to penalize their misclassification more heavily. In scikit-learn, the class_weight parameter adjusts the impurity calculation: $G_{\text{weighted}}(S) = \sum_{k=1}^c w_k p_k (1 - p_k), \quad H_{\text{weighted}}(S) = - \sum_{k=1}^c w_k p_k \log_2(p_k)$ where $w_k$ is the weight for class $k$ (e.g., inverse class frequency).
- This encourages splits that prioritize minority class purity.
Stratified Sampling:
- Use oversampling (e.g., duplicating minority class samples) or undersampling (e.g., reducing majority class samples) to balance the training data.
- Techniques like SMOTE (Synthetic Minority Oversampling Technique) generate synthetic minority samples, though these are typically used in ensembles.
- Ensure stratified sampling preserves the test set’s original distribution to avoid biased evaluation.
Modified Splitting Criteria:
- Use criteria like gain ratio (C4.5) to normalize impurity reductions, reducing bias toward majority class splits.
- Alternatively, adjust the Gini or entropy calculation to incorporate class weights directly, as above.
Tree Structure Adaptation:
- Decision trees can naturally create pure leaves for minority classes, but this may require deep trees, increasing overfitting risk. Pruning or ensemble methods (e.g., Random Forests, boosting) mitigate this.

3.4.3.3 Example

For a dataset with 95 negative and 5 positive samples:

Unweighted Gini: $p_{\text{neg}} = 0.95, \quad p_{\text{pos}} = 0.05$ $G(S) = 1 - (0.95^2 + 0.05^2) = 1 - (0.9025 + 0.0025) = 0.095$
Weighted Gini (e.g., weights $w_{\text{neg}} = 1, w_{\text{pos}} = 19$): Normalize weights: $w_{\text{neg}}' = \frac{1}{1+19} = 0.05, \quad w_{\text{pos}}' = \frac{19}{20} = 0.95$ Adjust proportions: $p_{\text{neg}}' = 0.95 \cdot 0.05, \quad p_{\text{pos}}' = 0.05 \cdot 0.95$ Compute weighted Gini accordingly.
A split isolating the positive class now has higher priority due to increased weight.

3.4.3.4 Properties

Class Weighting: Simple and effective, directly integrated into scikit-learn, but requires tuning weights.
Sampling: Balances data but may introduce noise (oversampling) or lose information (undersampling).
Modified Criteria: Gain ratio reduces bias but may be sensitive to imbalanced splits.
Practical Tip: Start with class weighting for moderate imbalance; use sampling or ensembles for extreme cases.

3.4.4 Practical Tips

Preprocess Thoughtfully: Clean data before training (e.g., impute missing values, encode categoricals) to improve performance, but leverage tree-specific strategies like surrogate splits to minimize preprocessing.
Handle Continuous Features Efficiently: Use C4.5 or CART’s thresholding for continuous features instead of discretization to preserve information.
Mitigate High-Cardinality Issues: For categorical features, consider target encoding or CHAID’s category merging to reduce overfitting.
Address Missing Values Strategically: Use surrogate splits (CART) or probabilistic assignment (C4.5) for robust handling; add missingness indicators to capture patterns.
Tackle Imbalance Early: Apply class weighting in scikit-learn (class_weight='balanced') or stratified sampling before resorting to complex methods like SMOTE.
Monitor Overfitting: High-cardinality features, missing values, or imbalanced data can lead to complex trees. Use pruning or ensembles to generalize better.
Leverage Robustness: Trees handle outliers well (isolating them in leaves), but noisy data can still create overly complex trees. Filter noise or use ensembles for stability.

Decision trees are robust to real-world data challenges but require careful handling to optimize performance:

Continuous vs. Categorical Features: Use thresholding for continuous features (C4.5, CART) and manage high-cardinality categoricals with binary splits (CART) or merging (CHAID).
Missing Values: Leverage surrogate splits (CART), probabilistic assignment (C4.5), or imputation with missingness indicators for flexibility.
Imbalanced Datasets: Apply class weighting or stratified sampling to prioritize minority class accuracy, with ensembles for extreme cases.

By applying these strategies, you can preprocess data effectively, mitigate biases, and build decision trees that generalize well to messy real-world datasets.

3.5 Pruning and Regularization

Decision trees, when left unchecked, tend to grow excessively complex, splitting until each leaf is pure or contains a single sample. This leads to overfitting, where the tree memorizes training data quirks, failing to generalize to unseen data. Pruning and regularization are essential techniques to combat this, balancing model complexity with predictive performance. Pruning can occur before tree growth (pre-pruning) or after (post-pruning), each with distinct mechanisms and trade-offs. This section explores these strategies, their mathematical foundations, and practical applications, building on the algorithms (ID3, C4.5, CART, CHAID) and data challenges discussed in Sections 3.3 and 3.4. We’ll provide detailed explanations, examples, and implementation tips to help you craft robust, interpretable decision trees that avoid the pitfalls of overfitting and underfitting.

We’ll cover the following topics:

Pre-Pruning: Using stopping criteria like max depth, min samples per leaf, and min impurity decrease.
Post-Pruning: Techniques like cost-complexity pruning and reduced-error pruning.
Trade-offs: Balancing overfitting vs. underfitting and interpretability vs. accuracy.

3.5.1 Pre-Pruning (Early Stopping)

3.5.1.1 Overview

Pre-pruning, or early stopping, halts tree growth before it becomes overly complex by imposing constraints during the splitting process. This approach is computationally efficient, as it avoids generating nodes that would later be pruned. However, setting appropriate thresholds requires careful tuning to avoid stopping too early (underfitting) or too late (overfitting).

3.5.1.2 Stopping Criteria

Pre-pruning relies on hyperparameters to control tree growth:

Maximum Depth (max_depth):
- Limits the number of splits from root to leaf (e.g., max_depth=5 allows up to 5 levels).
- Ensures shallow trees, enhancing interpretability but risking underfitting if set too low.
Minimum Samples per Leaf (min_samples_leaf):
- Requires each leaf to contain at least a specified number of samples (e.g., min_samples_leaf=5).
- Prevents splits that create small, overly specific leaves, reducing overfitting.
Minimum Samples to Split (min_samples_split):
- Requires a node to have at least a specified number of samples to consider splitting (e.g., min_samples_split=10).
- Similar to min_samples_leaf but applies to internal nodes.
Minimum Impurity Decrease (min_impurity_decrease):
- Only allows a split if the impurity reduction exceeds a threshold: $\Delta I = I(S) - \left( \frac{|S_L|}{|S|} I(S_L) + \frac{|S_R|}{|S|} I(S_R) \right) \geq \gamma$ where $I(S)$ is the impurity (e.g., Gini, entropy), $S_L$ and $S_R$ are child nodes, and $\gamma$ is the threshold.
- Ensures splits provide significant purity gains, avoiding marginal splits.

3.5.1.3 Example

Consider a dataset with 15 samples (10 red, 5 blue) and a potential split reducing Gini impurity from 0.444 to 0.1904 (as in Section 3.2.1.4):

If min_impurity_decrease=0.3, the split is rejected ($\Delta G = 0.444 - 0.1904 = 0.2536 < 0.3$).
If max_depth=2 and the current depth is 2, no further splits are allowed.
If min_samples_leaf=5 and a split creates a leaf with 3 samples, it is rejected.

3.5.1.4 Properties

Strengths: Computationally efficient, easy to implement, and widely supported (e.g., scikit-learn’s max_depth, min_samples_leaf).
Weaknesses: Heuristic thresholds may cause the horizon effect, where beneficial deeper splits are missed due to early stopping.
Practical Tip: Tune pre-pruning parameters via cross-validation to balance bias and variance. Start with max_depth=5 and min_samples_leaf=5 for reasonable regularization.

3.5.2 Post-Pruning

3.5.2.1 Overview

Post-pruning allows the tree to grow fully (or nearly fully) and then trims back branches that contribute little to generalization. This approach is more flexible than pre-pruning, as it evaluates the full tree’s structure before simplifying, but it is computationally more expensive due to the need to grow and then prune.

3.5.2.2 Cost-Complexity Pruning (CCP)

Used in CART, cost-complexity pruning balances training error and tree complexity using a cost function: $R_\alpha(T) = R(T) + \alpha \mid T\mid$ where:

$R(T)$: Training error (e.g., misclassification rate for classification, MSE for regression).
$\mid T\mid$: Number of leaves in the tree.
$\alpha$: Complexity parameter (non-negative, tuned via cross-validation).

Mechanism:

Grow a full tree $T_0$.
For increasing values of $\alpha$, compute the subtree $T_\alpha$ that minimizes $R_\alpha(T)$.
- This is done efficiently via weakest link pruning, iteratively removing the subtree that increases $R(T)$ the least per leaf removed.
Generate a sequence of subtrees $T_0, T_1, \ldots, T_k$, where each subtree is progressively simpler.
Select the subtree with the best validation performance (e.g., via cross-validation).

Example: For a tree with 10 leaves and misclassification error $R(T_0) = 0.05$:

Set $\alpha = 0.01$. Prune a subtree with 2 leaves if it increases error by less than $2 \cdot 0.01 = 0.02$.
Cross-validate to choose $\alpha$ yielding the lowest validation error.

3.5.2.3 Reduced-Error Pruning

This simpler post-pruning method, used in some implementations, prunes bottom-up:

Start at the leaves and evaluate each subtree.
Remove a subtree if pruning does not increase validation error beyond a threshold (e.g., no worse than unpruned performance).
Continue until no further prunes are beneficial.

Example: For a subtree with 2 leaves (error = 0.01), if pruning to a single leaf increases validation error to 0.02 (threshold = 0.015), retain the subtree.

3.5.2.4 Pessimistic Pruning (C4.5)

C4.5 uses pessimistic pruning, which adjusts the training error to account for overfitting:

Add a penalty (e.g., 0.5 errors per leaf) to estimate the true error: $R_{\text{pess}}(T) = R(T) + 0.5 \cdot |T|$
Prune a subtree if $R_{\text{pess}}$ does not increase significantly.

Example: A subtree with 3 leaves and error 0.03 has $R_{\text{pess}} = 0.03 + 0.5 \cdot 3 = 0.045$. If pruning to a leaf reduces $R_{\text{pess}}$, prune.

3.5.2.5 Properties

Cost-Complexity Pruning: Optimal balance of error and complexity, but requires cross-validation to tune $\alpha$.
Reduced-Error Pruning: Simpler but myopic, as it may miss globally optimal prunes.
Pessimistic Pruning: Conservative, reduces overfitting but may retain unnecessary branches.
Practical Tip: Use CCP in scikit-learn (ccp_alpha) for robust pruning; tune $\alpha$ via cross-validation for best results.

3.5.3 Trade-offs

3.5.3.1 Overfitting vs. Underfitting

Overfitting: Unpruned or lightly pruned trees (e.g., deep trees with pure leaves) have low training error but high variance, failing to generalize. For example, a tree with 100 leaves may perfectly fit training data but capture noise.
Underfitting: Overly strict pre-pruning (e.g., max_depth=1) or aggressive post-pruning (high $\alpha$) produces simple trees with high bias, missing important patterns.
Balance: Tune pre-pruning parameters or $\alpha$ to find a tree that minimizes validation error, balancing bias and variance.

3.5.3.2 Interpretability vs. Accuracy

Interpretability: Smaller trees (e.g., max_depth=3, ~8 leaves) are easier to understand and explain, ideal for applications like medical diagnostics or business rules.
Accuracy: Larger trees or lightly pruned trees may capture more patterns, improving training accuracy but risking overfitting and reduced interpretability.
Practical Tip: For interpretable models, prioritize pre-pruning with low max_depth. For accuracy, use post-pruning with cross-validated $\alpha$ or combine with ensembles.

3.5.3.3 Example

A tree with max_depth=10 fits training data perfectly (error = 0) but has high validation error (0.2). Setting max_depth=3 increases training error (0.1) but reduces validation error (0.12). CCP with $\alpha=0.01$ may yield a subtree with 5 leaves, balancing error (0.08) and simplicity.

3.5.4 Practical Tips

Start with Pre-Pruning: Use max_depth=5 and min_samples_leaf=5 as baselines in scikit-learn to prevent excessive growth.
Leverage Post-Pruning for Flexibility: Apply cost-complexity pruning (ccp_alpha) when you need optimal generalization, tuning via cross-validation.
Avoid Over-Pruning: Ensure pruning doesn’t eliminate valuable splits; monitor validation performance closely.
Enhance Interpretability: For human-readable models, limit depth or use pessimistic pruning (C4.5) to keep trees small.
Combine with Ensembles: Pruning is critical for single trees, but Random Forests or boosting further reduce overfitting by averaging multiple trees.
Tune via Cross-Validation: Use grid search over max_depth, min_samples_leaf, and ccp_alpha to find the best balance.
Monitor the Horizon Effect: Be cautious with strict pre-pruning, as it may miss deeper, beneficial splits.

Pruning and regularization are critical for building decision trees that generalize well:

Pre-Pruning: Uses stopping criteria like max_depth, min_samples_leaf, and min_impurity_decrease to limit growth, balancing efficiency and simplicity.
Post-Pruning: Techniques like cost-complexity pruning (CART) and reduced-error pruning optimize tree structure post-growth, leveraging cross-validation for robustness.
Trade-offs: Balance overfitting (complex trees) vs. underfitting (overly simple trees) and interpretability (small trees) vs. accuracy (larger trees).

By applying these techniques, you can control tree complexity, enhance generalization, and tailor models to your needs, whether for interpretable rules or high-performance predictions.

3.6 Strengths, Weaknesses, and Practical Tips

Decision trees are a cornerstone of machine learning, valued for their intuitive structure and versatility. However, like any model, they come with strengths that make them powerful in certain contexts and weaknesses that require careful management. This section dives into the key advantages and limitations of decision trees, providing a clear understanding of when and why to use them. We’ll also share practical tools and strategies, such as visualization techniques and methods for handling imbalanced datasets, to help you apply decision trees effectively in real-world scenarios. With illustrative explanations, mathematical insights where necessary, and actionable tips, this section ties together the concepts from Sections 3.2–3.5 (splitting criteria, algorithms, data challenges, and pruning) to equip you with the knowledge to leverage decision trees confidently.

We’ll cover the following:

Strengths: Interpretability, handling mixed data types, and robustness to outliers.
Weaknesses: Instability, sensitivity to data changes, and challenges with certain data types.
Practical Tools: Visualization, handling imbalances, and integration with ensembles.

3.6.1 Strengths

3.6.1.1 Interpretability

Decision trees are among the most interpretable machine learning models. Each prediction can be traced through a sequence of human-readable rules (e.g., “If Age ≤ 30 and Income > 50k, predict Positive”). This transparency makes trees ideal for applications where explainability is critical, such as medical diagnostics or business decision-making. For example, a doctor can explain a diagnosis by following the tree’s path, making it easier to justify to patients or stakeholders.

3.6.1.2 Handling Mixed Data Types

Unlike many models (e.g., linear regression, which requires numerical features and scaling), decision trees naturally handle both continuous and categorical features without preprocessing like one-hot encoding or normalization. As discussed in Section 3.4.1, continuous features are split via thresholds (e.g., $x \leq t$), while categorical features use multiway (ID3, C4.5, CHAID) or binary splits (CART). This flexibility simplifies data preparation, making trees suitable for datasets with mixed types, such as customer data with age (continuous) and region (categorical).

3.6.1.3 Capturing Non-Linear Relationships

Decision trees excel at modeling non-linear relationships by creating piecewise decision boundaries. For example, consider a dataset where the target depends on whether $x_1 > 5$ and $x_2 < 10$. A tree can capture this by splitting on $x_1$ and $x_2$, forming a rectangular decision region, whereas linear models struggle with such patterns. Mathematically, the tree approximates the decision function as a piecewise constant function: $f(x) = c_k \text{ if } x \in R_k$ where $R_k$ is a region defined by splits, and $c_k$ is the predicted class or value.

3.6.1.4 Modeling Feature Interactions

Trees naturally capture interactions between features. A split on feature $A$ under a node already split on feature $B$ creates a rule involving both (e.g., “If B > 2 and A ≤ 10”). This implicit interaction modeling is powerful for datasets where features jointly influence the target, without requiring explicit feature engineering (e.g., creating $A \cdot B$).

3.6.1.5 Robustness to Outliers

Decision trees are robust to outliers in the input space because outliers are typically isolated in their own leaves. For example, an extreme value like $x_1 = 1000$ may trigger a single split (e.g., $x_1 \leq 500$), isolating it without affecting other splits. This contrasts with linear models, where outliers can skew the entire model (e.g., shifting a regression line). Mathematically, the tree’s loss function (e.g., Gini impurity or MSE) is computed locally within nodes, limiting the impact of outliers: $G(S) = 1 - \sum_{k=1}^c p_k^2, \quad \text{Var}(S) = \frac{1}{\mid S\mid } \sum_{i \in S} (y_i - \bar{y})^2$

3.6.1.6 Minimal Data Preprocessing

Trees require little preprocessing. They don’t need feature scaling (since splits depend on order, not magnitude) and can handle missing values via strategies like surrogate splits or probabilistic assignment (Section 3.4.2). This makes trees a go-to choice for quick prototyping or datasets with raw, unprocessed features.

3.6.2 Weaknesses

3.6.2.1 Instability

Decision trees are unstable learners: small changes in the training data can lead to entirely different tree structures. This is due to the hierarchical nature of splitting—a change in an early split alters all subsequent splits. For example, adding a single sample might shift the optimal threshold for a top-level split, reshaping the entire tree. Mathematically, the greedy selection of splits: $\arg\max_{A,t} \Delta I(S, A, t)$ is sensitive to perturbations in $S$, leading to high variance. This instability reduces reliability for single trees, making ensembles critical for robust predictions.

3.6.2.2 Sensitivity to Data Changes

Related to instability, trees are sensitive to noise or small data changes. For instance, a noisy sample may cause a split that isolates it, creating an unnecessary branch. This sensitivity exacerbates overfitting, especially without pruning (Section 3.5). For example, a tree might split on a feature with many unique values (high cardinality) due to chance reductions in impurity, as noted in Section 3.2.3.

3.6.2.3 Poor Performance with Smooth Boundaries

Trees approximate decision boundaries with piecewise constant regions, which is suboptimal for smooth or linear boundaries. In regression, the prediction: $\hat{y} = \bar{y}_R \text{ for } x \in R$ is constant within each leaf region $R$, leading to “staircase” predictions that may poorly fit smooth trends (e.g., a linear relationship $y = 2x + 1$). In classification, a linear boundary requires multiple splits to approximate, increasing tree depth and complexity.

3.6.2.4 Bias Toward High-Cardinality Features

Algorithms like ID3, which use information gain: $IG(S, A) = H(S) - \sum_{v \in \text{values}(A)} \frac{\mid S_v\mid }{\mid S\mid } H(S_v)$ favor features with many unique values, as they produce more partitions, potentially reducing entropy more by chance. This bias, discussed in Section 3.2.3, is mitigated by gain ratio (C4.5) or binary splits (CART).

3.6.2.5 Challenges with High-Dimensional Sparse Data

In high-dimensional sparse datasets (e.g., text with thousands of features), single trees struggle to identify meaningful splits due to the curse of dimensionality. Methods like linear models or boosting are often more effective, as they handle sparsity better through regularization or iterative learning.

3.6.3 Practical Tools

3.6.3.1 Visualization

Visualizing decision trees is crucial for understanding their structure and debugging splits. Tools like:

Graphviz: Exports trees as DOT files for detailed, customizable visualizations.
Scikit-learn’s plot_tree: Generates quick, built-in tree plots.
Plotly: Creates interactive visualizations for exploring large trees.

Example: A tree splitting on “Age ≤ 30” and “Income > 50k” can be visualized to check if it’s splitting on irrelevant features (e.g., an ID field), prompting feature removal.

Implementation: Use scikit-learn’s plot_tree to visualize a tree, as shown below.

3.6.3.2 Handling Imbalanced Datasets

As discussed in Section 3.4.3, imbalanced datasets bias trees toward the majority class. Practical solutions include:

Class Weighting: Use class_weight='balanced' in scikit-learn to adjust impurity calculations: $G_{\text{weighted}}(S) = \sum_{k=1}^c w_k p_k (1 - p_k)$ where $w_k$ is the weight for class $k$ (e.g., inverse class frequency).
Stratified Sampling: Oversample the minority class or undersample the majority class to balance training data, preserving the test set’s original distribution.
SMOTE: Generate synthetic minority samples (typically used in ensembles).

3.6.3.3 Cross-Validation for Tuning

Always tune hyperparameters (e.g., max_depth, min_samples_leaf, ccp_alpha) using cross-validation to avoid under- or over-pruning. For example, grid search over:

max_depth: [3, 5, 10]
min_samples_leaf: [1, 5, 10]
ccp_alpha: [0.0, 0.01, 0.1] to find the combination minimizing validation error.

3.6.3.4 Integration with Ensembles

Single trees are unstable and prone to overfitting, but ensembles like Random Forests (bagging) and Gradient Boosting (boosting) mitigate these issues by combining multiple trees. Random Forests limit feature consideration at each split, reducing variance, while boosting iteratively corrects errors. These methods significantly improve accuracy over single trees.

3.6.3.5 Feature Importance and Interpretability

Trees provide feature importance scores based on the total impurity reduction from splits on each feature: $\text{Importance}(A) = \sum_{\text{nodes splitting on } A} \Delta I \cdot \frac{\mid S_{\text{node}}\mid }{\mid S\mid }$ This helps identify key predictors and enhances interpretability, even in ensembles. Partial dependence plots can further reveal how features influence predictions.

Decision trees offer unique strengths and face specific challenges:

Strengths: Highly interpretable, handle mixed data types, capture non-linear relationships and feature interactions, and are robust to outliers with minimal preprocessing.
Weaknesses: Unstable due to sensitivity to data changes, struggle with smooth boundaries, bias toward high-cardinality features, and less effective in high-dimensional sparse data.
Practical Tools: Use visualization (Graphviz, plot_tree), class weighting or sampling for imbalances, cross-validation for tuning, and ensembles for improved accuracy.

By understanding these characteristics and leveraging tools like visualization and ensemble methods, you can maximize the benefits of decision trees while mitigating their limitations. The next blog in the series will explore ensemble methods like Random Forests and boosting, which build on decision trees to achieve state-of-the-art performance.

Conclusion

Throughout this blog, we’ve embarked on a journey through the foundations of non-parametric models, exploring their flexibility, strengths, and challenges through the lenses of K-Nearest Neighbors (KNN) and decision trees. These models, free from rigid assumptions about data distributions, offer powerful tools for tackling complex, real-world problems. From the intuitive simplicity of KNN to the hierarchical elegance of decision trees, we’ve uncovered their core principles, practical applications, and limitations, setting the stage for the next leap in machine learning: ensemble methods. Let’s recap the key insights from each section and understand why decision trees serve as the bedrock for ensembles, paving the way for more robust and accurate predictive models.

In Section 1, we introduced non-parametric models, highlighting their key strength: flexibility. Unlike parametric models that assume specific functional forms (e.g., linear regression’s straight-line assumption), non-parametric models like KNN and decision trees adapt to the data’s inherent structure. We compared parametric and non-parametric approaches, noting that non-parametric models shine in scenarios with non-linear patterns or unknown distributions, such as image classification or customer segmentation. Their ability to scale with data complexity makes them ideal for diverse applications, from medical diagnostics to fraud detection, though they come with computational trade-offs.

Section 2 dove into KNN, the simplest non-parametric model, which relies on instance-based learning and distance-based decision-making. By predicting based on the majority class or average of the $k$ nearest neighbors, KNN offers an intuitive approach to classification and regression. However, we saw its limitations: the curse of dimensionality leads to sparse neighborhoods and unreliable distances in high-dimensional spaces, while its computational burden (storing and searching the entire dataset) hinders scalability. These challenges, coupled with KNN’s sensitivity to noise and lack of interpretability, naturally pivot us to tree-based models, which address many of these issues.

Section 3 explored decision trees in depth, establishing them as versatile, interpretable, and powerful non-parametric models. We began with their structure and terminology (Section 3.1), describing how root nodes, internal nodes, leaf nodes, and branches form interpretable decision paths. Visualizations like Graphviz or scikit-learn’s plot_tree make these paths tangible, revealing patterns like “If Experience < 3 years and Salary > 50k, predict High Turnover.” In Section 3.2, we unpacked the engine of decision trees: splitting criteria. From Gini impurity (CART) to entropy and information gain (ID3/C4.5), gain ratio, variance reduction, and chi-square splitting (CHAID), we saw how trees partition data to maximize homogeneity. Handling continuous features via thresholding and choosing between multiway and binary splits further refine their flexibility.

In Section 3.3, we examined classic decision tree algorithms—ID3, C4.5, CART, and CHAID. ID3’s simplicity suits categorical data but lacks pruning, while C4.5 extends it with continuous feature support, gain ratio, and pruning. CART’s binary splits and versatility for both classification and regression make it a modern staple, while CHAID’s statistical rigor excels in interpretable applications like marketing. Section 3.4 tackled data challenges, showing how trees handle continuous and categorical features, missing values (via surrogate splits or probabilistic assignment), and imbalanced datasets (through class weighting or sampling). Section 3.5 addressed overfitting with pre-pruning (e.g., max depth, min samples per leaf) and post-pruning (e.g., cost-complexity pruning), balancing model complexity with generalization. Finally, Section 3.6 highlighted decision trees’ strengths—interpretability, handling mixed data, and robustness to outliers—while acknowledging weaknesses like instability and poor performance with smooth boundaries or high-dimensional sparse data.

Motivation for Ensemble Methods

Decision trees, while powerful, have a critical Achilles’ heel: instability and high variance. As we saw in Section 3.6.2, small changes in the training data can drastically alter a tree’s structure, leading to inconsistent predictions. For example, a single noisy sample might shift a top-level split, reshaping the entire tree. Additionally, trees struggle with smooth decision boundaries, approximating them with piecewise constant regions, and can overfit without careful pruning. These limitations—instability, overfitting, and sensitivity to data changes—motivate the development of ensemble methods, which combine multiple decision trees to overcome these weaknesses while amplifying their strengths.

Why ensembles? Ensemble methods like Random Forests and Gradient Boosting leverage decision trees as their building blocks, addressing instability through aggregation. Random Forests use bagging (bootstrap aggregating) to train multiple trees on random subsets of the data and features, reducing variance by averaging predictions. This mitigates the impact of any single tree’s instability, as errors in individual trees tend to cancel out. Gradient Boosting, on the other hand, builds trees sequentially, with each tree correcting the errors of its predecessors, reducing bias and improving accuracy. Both approaches inherit decision trees’ strengths—interpretability, flexibility with mixed data, and robustness to outliers—while achieving state-of-the-art performance.

For instance, consider a classification problem where a single tree overfits by creating overly specific leaves for noisy samples. A Random Forest trains 100 trees, each on a different data subset, and aggregates their votes, smoothing out noise and stabilizing predictions. Similarly, Gradient Boosting iteratively refines predictions, focusing on misclassified samples to improve accuracy, especially for imbalanced datasets (Section 3.4.3). These methods also address high-dimensional sparse data (Section 3.6.2.5) by randomly selecting features or optimizing loss functions iteratively, making them more robust than single trees.

Decision trees are the bedrock of ensemble methods because their simplicity, flexibility, and interpretability make them ideal components for aggregation. Their hierarchical structure allows ensembles to capture complex patterns through diverse splits across multiple trees, while techniques like feature importance (Section 3.6.3.5) extend interpretability to ensembles. By combining trees, ensembles overcome the limitations of single trees—instability, overfitting, and poor boundary approximation—while retaining their intuitive appeal. This makes decision trees a natural stepping stone to advanced machine learning models, where we’ll explore Random Forests, Gradient Boosting, and other ensemble techniques in detail.

Non-parametric models like KNN and decision trees offer a powerful starting point for machine learning, balancing flexibility with interpretability. KNN’s simplicity is intuitive but limited by dimensionality and computational cost, while decision trees provide a robust, interpretable framework for handling complex data. By mastering their splitting criteria, algorithms, data handling, pruning, and practical tools, you can build models that are both effective and explainable. However, the limitations of single trees—particularly their instability and tendency to overfit—highlight the need for ensembles, which combine the best of decision trees into more accurate, stable, and scalable models. As we move to ensemble methods, you’ll see how decision trees evolve from standalone tools to the foundation of some of the most powerful algorithms in modern machine learning, ready to tackle the toughest predictive challenges.